Descrizione Molle di tensione simbolo formula

Prima di interpretare il molla di estensione deve essere chiarito se il tipo di stress previsto è a statico o a stress dinamico atti.

Non è possibile fornire valori generali di resistenza alla fatica per carichi dinamici su molle a trazione, poiché il Punti di flessione degli occhielli possono verificarsi ulteriori sollecitazioni, alcune delle quali superano le sollecitazioni consentite. Pertanto, se possibile, le molle di trazione devono essere soggette solo a carichi statici. Se lo stress dinamico non può essere evitato, si dovrebbe optare per l’angolo Occhielli rinunciare e terminali laminati o avvitati distribuire. Quando le molle di trazione sono soggette a carichi dinamici, è importante una prova di durata in condizioni operative successive. Un rinforzo superficiale mediante pallinatura non può essere eseguito o solo con grande sforzo a causa delle spire ravvicinate.

Table of Contents

Sollecitazione statica sulla molla di estensione

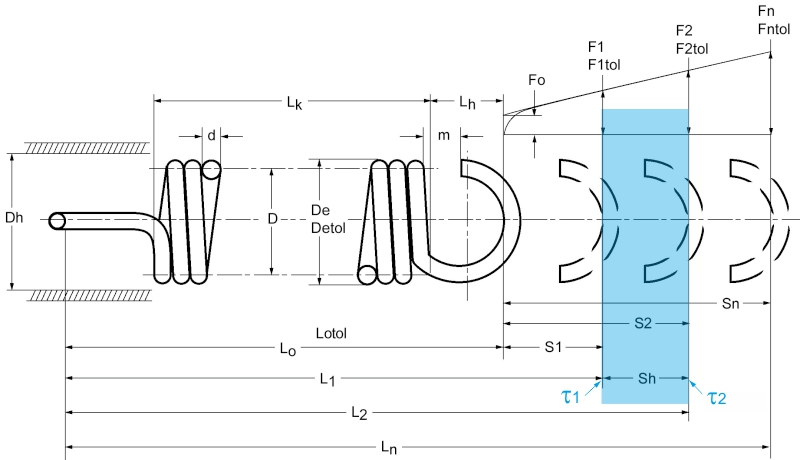
Carico (statico) costante nel tempo o carico variabile nel tempo con meno di 10.000 corse in totale o sollecitazioni di corsa ridotta (τh = τ2 – τ1) fino a 0,1 x resistenza alla fatica (τkh = τk2 – τk1).

Sollecitazione dinamica sulla molla di estensione

Le sollecitazioni dinamiche sulle molle sono definite come sollecitazioni che cambiano nel tempo con più di 10.000 variazioni di carico o sollecitazioni della corsa (τh) superiori a 0,1 x resistenza alla fatica (τkh) con sollecitazione della corsa costante e variabile.

Lo sforzo di taglio esistente viene determinato come segue.

Sforzo di taglio dalla forza: $\ tau = \ frac wpml_curved wpml_value = '8DF' / wpml_curved {\ pi d ^ wpml_curved wpml_value = '3' / wpml_curved }$

Sforzo di taglio dal percorso: $\ tau = \ frac wpml_curved wpml_value = 'Gds' / wpml_curved {\ pi nD ^ wpml_curved wpml_value = '2' / wpml_curved }$

Per il carico dinamico, la tensione della corsa corretta deve essere calcolata a causa dell’aumento della tensione.

Sforzo di taglio corretto: $\ dew_ {} = k \ tau$

Tensione di corsa corretta: τkh = τk2 – τk1

Dove per k si applica (secondo Bergsträsser):

$k = \ frac {\ frac wpml_curved wpml_value = 'D' / wpml_curved wpml_curved wpml_value = 'd' / wpml_curved +0,5} {\ frac wpml_curved wpml_value = 'D' / wpml_curved wpml_curved wpml_value = 'd' / wpml_curved -0,75}$

Con il fattore di correzione della tensione k, che dipende dal rapporto di avvolgimento (rapporto tra diametro medio e spessore del filo) della molla, è possibile determinare approssimativamente la tensione massima.

Tensione ammissibile: $\ dew_ {} = 0,45 \ cdot R_ {}$

Valori minimi di resistenza alla trazione dei materiali delle molle $R_ {}$

La tensione massima esistente τn alla massima flessione della molla sn è equiparata alla sollecitazione ammissibile. Comunque rilassamento Per evitare ciò, solo l’80% di questo viaggio primaverile dovrebbe essere utilizzato nella pratica.

$s_ {} = 0,8 \ cdot s_ {}$