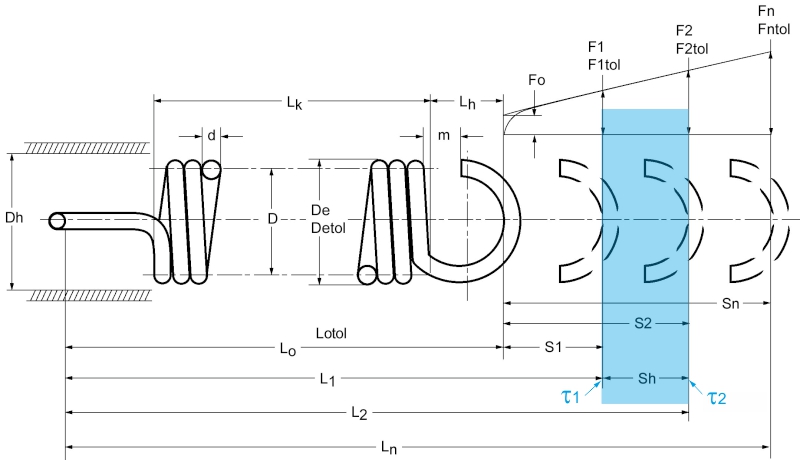
Description Formula symbol tension springs

Before interpreting the extension spring it must be clarified whether the intended type of stress is a static or a dynamic stress acts.

No general fatigue strength values can be given for dynamic loads on tension springs, as the Bending points of the eyelets additional stresses can occur, some of which exceed the permissible stresses. Tension springs should therefore only be subjected to static loads if possible. If dynamic stress cannot be avoided, one should go for angled Eyelets renounce and rolled or screwed in end pieces deploy. When tension springs are subjected to dynamic loads, a life test under later operating conditions is important. A surface strengthening by shot peening cannot be carried out or only with great effort because of the closely spaced turns.

Table of Contents

Static stress on extension spring

Time-constant (static) load or time-variable load with less than 10,000 strokes in total or small stroke stresses (τh = τ2 – τ1) up to 0.1 x fatigue strength (τkh = τk2 – τk1).

Dynamic stress on extension spring

Dynamic stress on springs is defined as stresses that change over time with more than 10,000 load changes or stroke stresses (τh) over 0.1 x fatigue strength (τkh) with constant and variable stroke stress.

The existing shear stress is determined as follows.

Shear stress from force: $\tau=\frac<wpml_curved wpml_value='8DF'></wpml_curved>{\pi d^<wpml_curved wpml_value='3'></wpml_curved>}$

Shear stress from path: $\tau=\frac<wpml_curved wpml_value='Gds'></wpml_curved>{\pi nD^<wpml_curved wpml_value='2'></wpml_curved>}$

For the dynamic load, the corrected stroke tension must be calculated because of the increase in tension.

Corrected shear stress : $\dew_{ } = k \ tau$

Corrected stroke voltage: τkh = τk2 – τk1

Where for k applies (according to Bergsträsser):

$k=\frac{\frac<wpml_curved wpml_value='D'></wpml_curved><wpml_curved wpml_value='d'></wpml_curved>+0,5}{\frac<wpml_curved wpml_value='D'></wpml_curved><wpml_curved wpml_value='d'></wpml_curved>-0,75}$

With the tension correction factor k, which depends on the winding ratio (ratio of mean diameter to wire thickness) of the spring, the highest tension can be approximately determined.

Allowable voltage: $\dew_{ } = 0.45 \ cdot R_ { }$

Minimum tensile strength values of spring materials $R_ { }$

The existing maximum stress τn at the greatest spring deflection sn is equated with the permissible stress. To however relaxation To avoid this, only 80% of this spring travel should be used in practice.

$s_ { } = 0.8 \ cdot s_ { }$