Antes de interpretar el Resorte de compresión Básicamente, conviene aclarar si el tipo de esfuerzo pretendido es estático, cuasiestático o dinámico.
Table of Contents
Esfuerzo estático o cuasiestático
Carga constante en el tiempo (estática) o carga variable en el tiempo con menos de 10.000 carreras en total o tensiones de carrera pequeñas de hasta 0,1 x resistencia a la fatiga (τkh = τk2 -τk1).
Estrés dinámico
La tensión dinámica en los resortes se define como tensiones que varían con el tiempo con más de 10,000 cambios de carga o tensiones de carrera superiores a 0,1 x resistencia a la fatiga (τkh) con tensión de carrera constante y variable. El resorte está en su mayoría pretensado y expuesto a cargas de oleaje periódicas con una curva sinusoidal que ocurren aleatoriamente (estocásticamente), como es el caso de la suspensión de vehículos.
Dependiendo del número requerido de ciclos de carga «N» sin interrupción, se diferencia:
1. El área de Resistencia a la fatiga con número de ciclos de carga
N ≥ 10 Séptimo para muelles conformados en frío
N ≥ 2 x 10 Sexto para muelles termoformados
Con voltaje de carrera menor que la resistencia a la fatiga.
2. El área de Resistencia a la fatiga con número de ciclos de carga
norte< 10 Séptimo para muelles conformados en frío
norte< 2 x 10 Sexto para muelles termoformados
Con un voltaje de carrera mayor que la resistencia a la fatiga y menor que la resistencia al tiempo.
El esfuerzo cortante existente se determina como sigue.
Esfuerzo cortante por fuerza: \Large \tau=\frac{8DF}{\pi d^{3}}
Esfuerzo cortante de la trayectoria: \Large \tau=\frac{Gds}{\pi nD^{2}}
Descripción Fórmula símbolo resortes de compresión [PDF]
Para resortes de compresión cargados dinámicamente, se aplica el esfuerzo cortante corregido debido al aumento resultante en el esfuerzo. Con el factor de corrección de tensión k, que depende de la relación de bobinado (relación entre el diámetro medio y el grosor del alambre) del resorte, se puede determinar aproximadamente la tensión más alta.
Esfuerzo cortante corregido :
τk1 = k · τ1< τko
τk2 = k · τ2< τko
donde se aplica k (según Bergsträsser)
\Large k=\frac{\frac{D}{d}+0,5}{\frac{D}{d}-0,75}
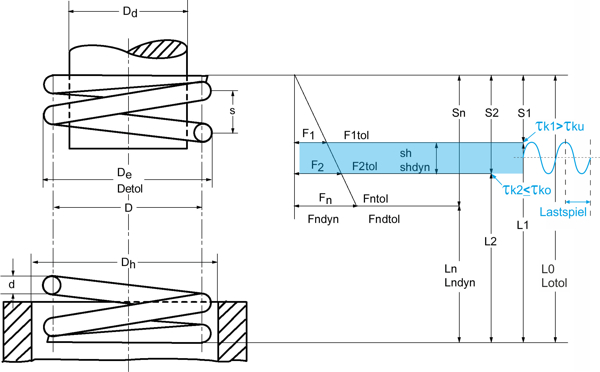
La tensión superior permitida τko para cada tipo de material de resorte se lee en el diagrama de resistencia a la fatiga (diagrama de Goodman) de DIN EN 13906-1 (Fig. 12 a Fig. 22).
La carrera de trabajo deseada no debe exceder la resistencia a la fatiga (τkh):
τkh = τk2 – τk1< τkhzul
Con el Programa de cálculo de muelles Gutekunst WinFSB cada resorte de compresión calculado también se puede calcular para la aplicación dinámica. Todo lo que tienes que hacer es activar la opción «permanente» y «shot peened». Los valores dinámicos y el diagrama de Goodman se muestran en el área «Estrés».
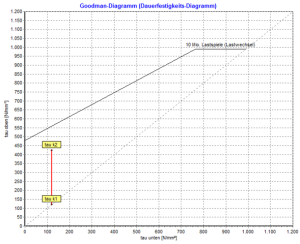
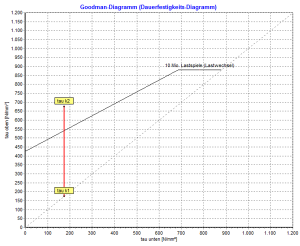
¡Importante!
La tensión del bloque τczul también debe comprobarse para tener en cuenta la superposición de la tensión debida a las vibraciones naturales del cuerpo del resorte con resortes de compresión cargados dinámicamente.
Los resortes de compresión tensados dinámicamente deben someterse a granallado antes de su uso. El granallado comprime las capas superficiales de modo que se consigue una resistencia a la fatiga significativamente mejor.
Para la resistencia a la fatiga de un resorte de compresión, los normales son particularmente adecuados para aplicaciones de dinámica media. Alambre de acero para muelles EN 10270-1DH y SH, así como los cables de resorte de válvula EN 10270-2-VDC, -VDSiCr y -VDCrV para aplicaciones de alta dinámica.
Una vez que la corrosión o la fricción han pasado Mandril o manga actúa sobre el resorte de compresión, la resistencia a la fatiga ya no está garantizada.
Información Adicional: