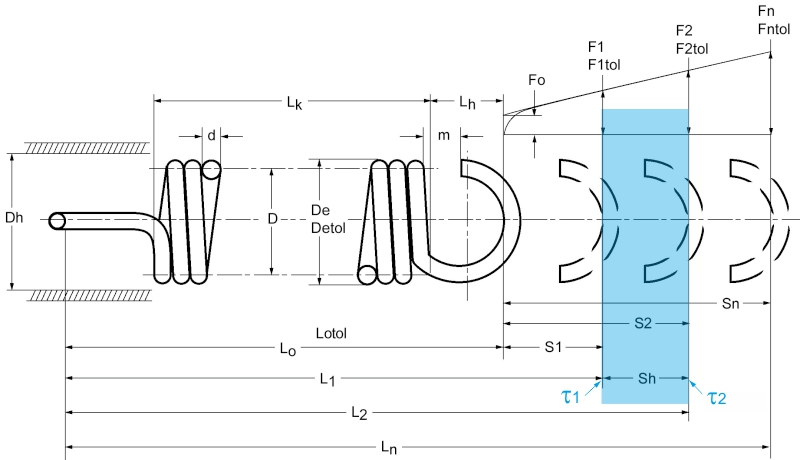
Descripción Fórmula símbolo resortes de tensión

Antes de interpretar el resorte de extensión Debe aclararse si el tipo de estrés pretendido es un estático o un estrés dinámico hechos.

No se pueden dar valores generales de resistencia a la fatiga para cargas dinámicas en resortes de tracción, ya que Puntos de flexión de los ojales Pueden ocurrir tensiones adicionales, algunas de las cuales exceden las tensiones permisibles. Por lo tanto, los resortes de tensión solo deben someterse a cargas estáticas si es posible. Si no se puede evitar el estrés dinámico, se debe optar por Ojales renunciar y enrollado o atornillado en las piezas de los extremos desplegar. Cuando los resortes de tensión están sujetos a cargas dinámicas, es importante realizar una prueba de vida en condiciones de funcionamiento posteriores. Un refuerzo de la superficie por shot peening no se puede realizar o solo con un gran esfuerzo debido a los giros poco espaciados.

Table of Contents

Tensión estática en el resorte de extensión

Carga constante en el tiempo (estática) o carga variable en el tiempo con menos de 10,000 carreras en esfuerzos de carrera pequeños o totales (τh = τ2 – τ1) hasta 0.1 x resistencia a la fatiga (τkh = τk2 – τk1).

Tensión dinámica en el resorte de extensión

La tensión dinámica en los resortes se define como tensiones que cambian con el tiempo con más de 10,000 cambios de carga o tensiones de carrera (τh) sobre 0,1 x resistencia a la fatiga (τkh) con tensión de carrera constante y variable.

El esfuerzo cortante existente se determina como sigue.

Esfuerzo cortante por fuerza: $\ tau = \ frac wpml_curved wpml_value = '8DF' / wpml_curved {\ pi d ^ wpml_curved wpml_value = '3' / wpml_curved }$

Esfuerzo cortante de la trayectoria: $\ tau = \ frac wpml_curved wpml_value = 'Gds' / wpml_curved {\ pi nD ^ wpml_curved wpml_value = '2' / wpml_curved }$

Para la carga dinámica, la tensión de carrera corregida debe calcularse debido al aumento de tensión.

Esfuerzo cortante corregido: $\ rocío_ {} = k \ tau$

Voltaje de carrera corregido: τkh = τk2 – τk1

Donde se aplica k (según Bergsträsser):

$k = \ frac {\ frac wpml_curved wpml_value = 'D' / wpml_curved wpml_curved wpml_value = 'd' / wpml_curved +0,5} {\ frac wpml_curved wpml_value = 'D' / wpml_curved wpml_curved wpml_value = 'd' / wpml_curved -0,75}$

Con el factor de corrección de tensión k, que depende de la relación de bobinado (relación entre el diámetro medio y el grosor del alambre) del resorte, se puede determinar aproximadamente la tensión más alta.

Voltaje admisible: $\ dew_ {} = 0.45 \ cdot R_ {}$

Valores mínimos de resistencia a la tracción de materiales de resorte $R_ {}$

La tensión máxima existente τn en la mayor deflexión del resorte sn se equipara con la tensión permisible. Sin embargo relajación Para evitar esto, solo el 80% de este recorrido del resorte debe usarse en la práctica.

$s_ {} = 0.8 \ cdot s_ {}$