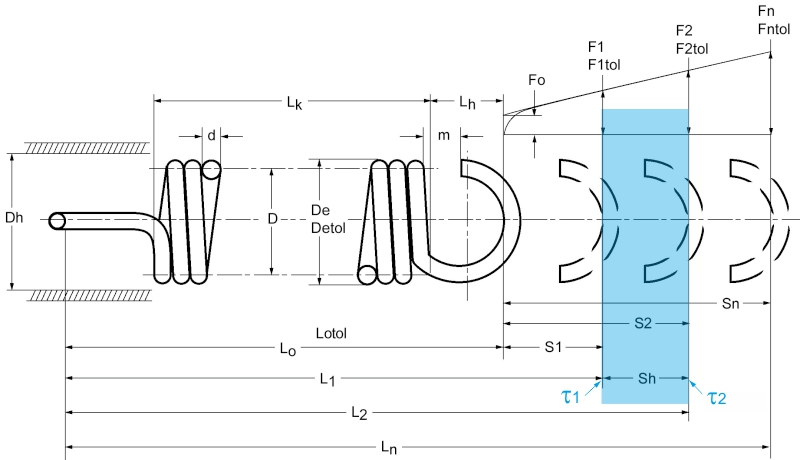
Description Symbole de formule Ressorts de tension

Avant d’interpréter le ressort de traction il faut clarifier si le type de stress prévu est un statique ou un contrainte dynamique actes.

Aucune valeur générale de résistance à la fatigue ne peut être donnée pour les charges dynamiques sur les ressorts de traction, Points de pliage des œillets des contraintes supplémentaires peuvent survenir, dont certaines dépassent les contraintes admissibles. Les ressorts de tension ne doivent donc être soumis à des charges statiques que si possible. Si le stress dynamique ne peut être évité, il faut opter pour un angle Oeillets renoncer et roulé ou vissé en bouts déployer. Lorsque les ressorts de tension sont soumis à des charges dynamiques, un test de durée de vie dans des conditions de fonctionnement ultérieures est important. Un renforcement de surface par grenaillage ne peut pas être réalisé ou seulement avec un effort important en raison des spires rapprochées.

Table of Contents

Contrainte statique sur le ressort de traction

Charge constante dans le temps (statique) ou charge variable dans le temps avec moins de 10000 courses au total ou petites contraintes de course (τh = τ2 – τ1) jusqu’à 0,1 x résistance à la fatigue (τkh = τk2 – τk1).

Contrainte dynamique sur le ressort de traction

Les contraintes dynamiques sur les ressorts sont définies comme des contraintes qui changent dans le temps avec plus de 10 000 changements de charge ou des contraintes de course (τh) supérieures à 0,1 x résistance à la fatigue (τkh) avec une contrainte de course constante et variable.

La contrainte de cisaillement existante est déterminée comme suit.

Contrainte de cisaillement due à la force: $\ tau = \ frac wpml_curved wpml_value = '8DF' / wpml_curved {\ pi d ^ wpml_curved wpml_value = '3' / wpml_curved }$

Contrainte de cisaillement du chemin: $\ tau = \ frac wpml_curved wpml_value = 'Gds' / wpml_curved {\ pi nD ^ wpml_curved wpml_value = '2' / wpml_curved }$

Pour la charge dynamique, la tension de course corrigée doit être calculée en raison de l’augmentation de la tension.

Contrainte de cisaillement corrigée: $\ dew_ {} = k \ tau$

Tension de course corrigée: τkh = τk2 – τk1

Où pour k s’applique (selon Bergsträsser):

$k = \ frac {\ frac wpml_curved wpml_value = 'D' / wpml_curved wpml_curved wpml_value = 'd' / wpml_curved +0,5} {\ frac wpml_curved wpml_value = 'D' / wpml_curved wpml_curved wpml_value = 'd' / wpml_curved -0,75}$

Avec le facteur de correction de tension k, qui dépend du rapport d’enroulement (rapport du diamètre moyen à l’épaisseur du fil) du ressort, la tension la plus élevée peut être approximativement déterminée.

Tension admissible: $\ dew_ {} = 0,45 \ cdot R_ {}$

Valeurs minimales de résistance à la traction des matériaux de ressort $R_ {}$

La contrainte maximale existante τn à la plus grande déformation du ressort sn correspond à la contrainte admissible. Pour cependant relaxation Pour éviter cela, seulement 80% de cette course de ressort doit être utilisée en pratique.

$s_ {} = 0.8 \ cdot s_ {}$