A. Értelmezése előtt Nyomórugó Alapvetően tisztázni kell, hogy a kívánt típusú stressz statikus, kvázi-statikus vagy dinamikus-e.
Table of Contents
Statikus vagy kvázi-statikus stressz
Időállandó (nyugalmi) terhelés vagy időváltoztató terhelés kevesebb, mint 10 000 löket teljes vagy kicsi löketfeszültségein, akár 0,1-szeres fáradtsági erővel (τkh = τk2 -τk1).
Dinamikus stressz
A rugók dinamikus feszültségét olyan stresszként definiáljuk, amely idővel változik, több mint 10 000 terhelésváltozással, vagy a löketfeszültségeket, amelyek 0,1 x fáradtsági erő (τkh) felett vannak állandó és változó löketfeszültség mellett. A rugó többnyire előfeszített és szinuszos görbével történő periodikus duzzadási terheléseknek van kitéve, amelyek véletlenszerűen (sztochasztikusan) fordulnak elő, ahogy a jármű felfüggesztése is.
A szükséges „N” terhelési ciklusok szünet nélküli számától függően megkülönböztethetők:
1. A terület Kifáradási szilárdság a terhelési ciklusok számával
N ≥ 10 7. hidegen alakított rugókhoz
N ≥ 2 x 10 6. hőformázott rugókhoz
A fáradási szilárdságnál kisebb löketfeszültség mellett.
2. A terület Kifáradási szilárdság a terhelési ciklusok számával
N< 10. 7. hidegen alakított rugókhoz
N< 2 x 10 6. hőformázott rugókhoz
A fáradási szilárdságnál nagyobb és az időbeli löketnél kisebb löketfeszültségnél
A meglévő nyírófeszültséget a következőképpen határozzuk meg.
Nyírófeszültség az erőtől: \Large \tau=\frac{8DF}{\pi d^{3}}
Nyírófeszültség az útról: \Large \tau=\frac{Gds}{\pi nD^{2}}
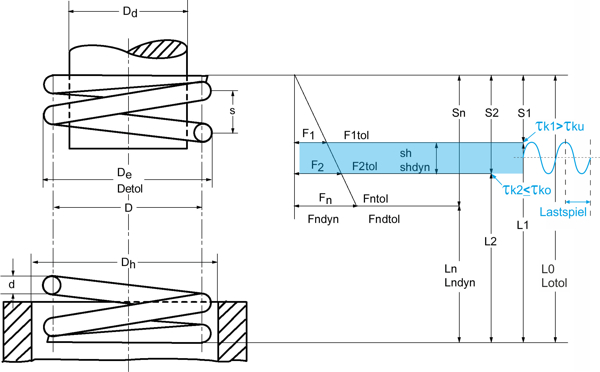
Leírás Képlet szimbólum kompressziós rugók [PDF]
Dinamikusan terhelt kompressziós rugók esetében a korrigált nyírófeszültség érvényesül az ebből fakadó stressznövekedés miatt. A rugó tekercselési arányától (az átlagos átmérő és a huzalvastagság arányától) függő k feszültségkorrekciós tényezővel a legnagyobb feszültség hozzávetőlegesen meghatározható.
Korrigált nyírófeszültség :
τk1 = k · τ1< τko
τk2 = k · τ2< τko
ahol a k vonatkozik (Bergsträsser szerint)
\Large k=\frac{\frac{D}{d}+0,5}{\frac{D}{d}-0,75}
Az egyes rugóanyag-típusok megengedett felső feszültsége a DIN EN 13906-1 (12. és 22. ábra) fáradási szilárdsági diagramjáról (Goodman diagram) olvasható le.
A kívánt üzemi löket nem haladhatja meg a fáradási szilárdságot (τkh):
τkh = τk2 – τk1< τkhzul
A … val Gutekunst tavaszi számítási program WinFSB minden kiszámított nyomórugó kiszámítható a dinamikus alkalmazáshoz is. Csak annyit kell tennie, hogy aktiválja az „állandó” és a „lövés finom” opciókat. Ezután a dinamikus értékek és a Goodman diagram megjelenik a „Stressz” területen.
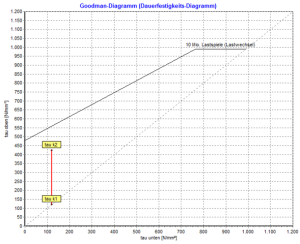
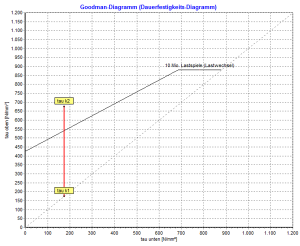
Fontos!
Az τczul blokkfeszültséget is ellenőrizni kell, hogy figyelembe vegyük a rugótest természetes rezgéséből adódó feszültség egymásra épülését dinamikusan megterhelt nyomórugókkal.
A dinamikusan igénybevett kompressziós rugókat használat előtt le kell rúgni. A lövéscsiszolás összenyomja a felületi rétegeket, így lényegesen jobb fáradási szilárdság érhető el.
A nyomórugó fáradási szilárdságához a normál rugók különösen alkalmasak közepesen dinamikus alkalmazásokhoz Rugós acélhuzal EN 10270-1DH és SH, valamint az EN 10270-2-VDC, -VDSiCr és -VDCrV szeleprugós vezetékek nagy dinamikus alkalmazásokhoz.
Miután a korrózió vagy a súrlódás átment Tüske vagy hüvely hat a nyomórugóra, a fáradási szilárdság már nem garantált!
További információ: