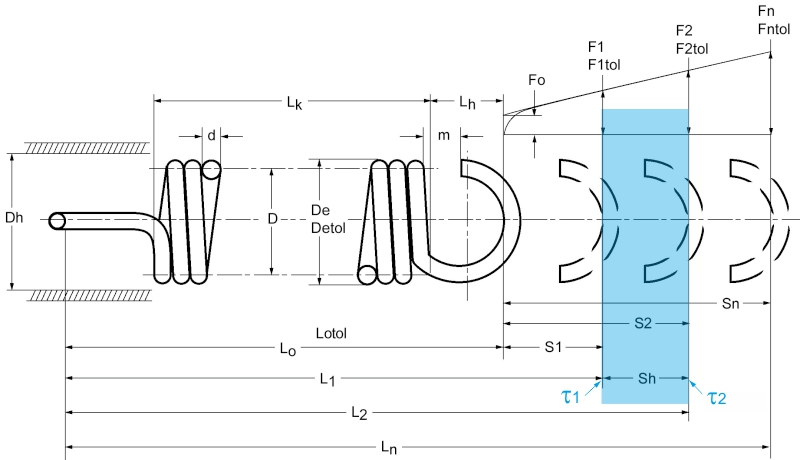
Leírás A Formula szimbólum feszítő rugói

A. Értelmezése előtt hosszabbító rugó tisztázni kell, hogy a kívánt típusú stressz a statikus vagy a dinamikus stressz cselekmények.

A feszítő rugók dinamikus terhelésére nem adható általános fáradási szilárdsági érték, mivel a A fűzőlyukak hajlítási pontjai további feszültségek léphetnek fel, amelyek némelyike meghaladja a megengedett feszültségeket. A feszítő rugókat ezért csak statikus terhelésnek lehet kitenni, ha lehetséges. Ha a dinamikus stressz nem kerülhető el, akkor hajlítottnak kell lennie Fűzőlyukak lemondani és végdarabokba tekerve vagy csavarva bevetni. Amikor a feszítőrugókat dinamikus terhelésnek vetik alá, fontos az élettartam vizsgálata későbbi üzemi körülmények között. A felület erősítése lövéses aprítással nem végezhető el, vagy csak nagy erőfeszítéssel, a szorosan elhelyezett fordulatok miatt.

Table of Contents

Statikus feszültség a hosszabbító rugón

Időállandó (statikus) terhelés vagy időben változó terhelés kevesebb, mint 10 000 löket teljes vagy kis löketfeszültségnél (τh = τ2 – τ1) 0,1 x fáradtsági erőig (τkh = τk2 – τk1).

Dinamikus feszültség a hosszabbító rugón

A rugók dinamikus feszültségét olyan feszültségekként definiáljuk, amelyek idővel több mint 10 000 terhelésváltozással változnak, vagy löketfeszültségek (τh) 0,1 x fáradási szilárdság (τkh) felett állandó és változó löketfeszültség mellett.

A meglévő nyírófeszültséget a következőképpen határozzuk meg.

Nyírófeszültség az erőtől: $\ tau = \ frac wpml_curved wpml_value = '8DF' / wpml_curved {\ pi d ^ wpml_curved wpml_value = '3' / wpml_curved }$

Nyírófeszültség az útról: $\ tau = \ frac wpml_curved wpml_value = 'Gds' / wpml_curved {\ pi nD ^ wpml_curved wpml_value = '2' / wpml_curved }$

A dinamikus terheléshez a korrigált löketfeszültséget a feszültség növekedése miatt kell kiszámítani.

Korrigált nyírófeszültség: $\ harmat_ {} = k \ tau$

Korrigált löketfeszültség: τkh = τk2 – τk1

Ahol a k vonatkozik (Bergsträsser szerint):

$k = \ frac {\ frac wpml_curved wpml_value = 'D' / wpml_curved wpml_curved wpml_value = 'd' / wpml_curved +0,5} {\ frac wpml_curved wpml_value = 'D' / wpml_curved wpml_curved wpml_value = 'd' / wpml_curved -0,75}$

A rugó tekercselési arányától (az átlagos átmérő és a huzalvastagság arányától) függő k feszültségkorrekciós tényezővel megközelítőleg meghatározható a legnagyobb feszültség.

Megengedett feszültség: $\ dew_ {} = 0,45 \ cdot R_ {}$

A rugóanyagok minimális szakítószilárdsági értékei $R_ {}$

A legnagyobb τn feszültséget az sn legnagyobb rugóhajlításnál a megengedett feszültséggel egyenlítik. Ahhoz azonban kikapcsolódás Ennek elkerülése érdekében a tavaszi utazásnak csak a 80% -át szabad felhasználni a gyakorlatban.

$s_ {} = 0,8 \ cdot s_ {}$