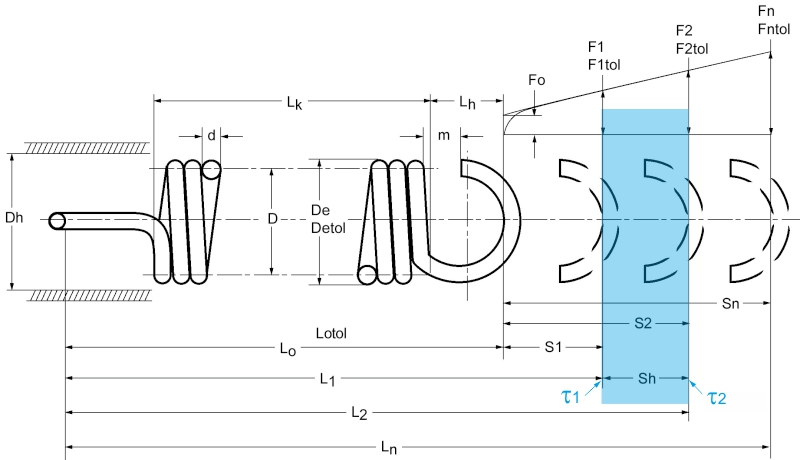
Popis Symbol napínacích pružin
Před interpretací tažná pružina je třeba objasnit, zda je zamýšleným typem stresu a statický nebo a dynamické napětí činy.
Pro dynamická zatížení na tažné pružiny nelze uvést žádné obecné hodnoty únavové pevnosti, např Ohybové body očka mohou nastat další napětí, z nichž některá překračují povolená napětí. Tažné pružiny by proto měly být pokud možno vystaveny statickému zatížení. Pokud se nelze vyhnout dynamickému namáhání, mělo by se jednat o úhel Očka zřeknout se a válcované nebo našroubované koncové díly nasadit. Pokud jsou tažné pružiny vystaveny dynamickému zatížení, je důležitá zkouška životnosti za pozdějších provozních podmínek. Zesílení povrchu tryskáním nelze provést nebo jen s velkým úsilím kvůli těsně rozmístěným zatáčkám.
Table of Contents
Statické namáhání tažné pružiny
Časově konstantní (statické) zatížení nebo časově proměnné zatížení s méně než 10 000 zdvihy celkového nebo malého zdvihu (τh = τ2 – τ1) až 0,1 x únavová pevnost (τkh = τk2 – τk1).
Dynamické namáhání tažné pružiny
Dynamické napětí na pružinách je definováno jako napětí, které se v průběhu času mění s více než 10 000 změnami zatížení nebo tahová napětí (τh) nad 0,1 x únavová pevnost (τkh) s konstantním a proměnným tahovým napětím.
Stávající smykové napětí se stanoví následovně.
Smykové napětí od síly:
Smykové napětí z dráhy:
U dynamického zatížení je třeba vypočítat opravené napětí zdvihu z důvodu zvýšení napětí.
Opravené smykové napětí:
Opravené zdvihové napětí: τkh = τk2 – τk1
Kde platí k (podle Bergsträssera):
Pomocí korekčního faktoru napětí k, který závisí na poměru vinutí (poměr středního průměru k tloušťce drátu) pružiny, lze přibližně určit nejvyšší napětí.
Přípustné napětí:
Minimální hodnoty pevnosti v tahu pružinových materiálů
Stávající maximální napětí τn při největším vychýlení pružiny sn se rovná přípustnému napětí. K tomu relaxace Aby se tomu zabránilo, mělo by se v praxi použít pouze 80% tohoto pojezdu pružiny.
Zajímavé odkazy: