Avant d’interpréter le Ressort de compression Il convient essentiellement de clarifier si le type de contrainte prévu est statique, quasi-statique ou dynamique.
Table of Contents
Contrainte statique ou quasi-statique
Charge constante de temps (au repos) ou charge variable dans le temps avec moins de 10 000 courses au total ou petites contraintes de course allant jusqu’à 0,1 x résistance à la fatigue (τkh = τk2 -τk1).
Stress dynamique
La contrainte dynamique dans les ressorts est définie comme une contrainte qui change au fil du temps avec plus de 10 000 changements de charge ou des contraintes de course supérieures à 0,1 x résistance à la fatigue (τkh) avec une contrainte de course constante et variable. Le ressort est principalement prétendu et exposé à des charges de houle périodiques avec une courbe sinusoïdale qui se produisent de manière aléatoire (stochastiquement), comme c’est le cas avec la suspension de véhicule.
En fonction du nombre de cycles de charge « N » requis sans interruption, on différencie:
1. La zone de Résistance à la fatigue avec nombre de cycles de charge
N ≥ 10 7e pour ressorts formés à froid
N ≥ 2 x 10 6e pour ressorts thermoformés
Avec une tension de course inférieure à la résistance à la fatigue.
2. La zone de Résistance à la fatigue avec nombre de cycles de charge
N< dix 7e pour ressorts formés à froid
N< 2 x 10 6e pour ressorts thermoformés
Avec une tension de course supérieure à la résistance à la fatigue et inférieure à la force de course dans le temps
La contrainte de cisaillement existante est déterminée comme suit.
Contrainte de cisaillement due à la force: \Large \tau=\frac{8DF}{\pi d^{3}}
Contrainte de cisaillement du chemin: \Large \tau=\frac{Gds}{\pi nD^{2}}
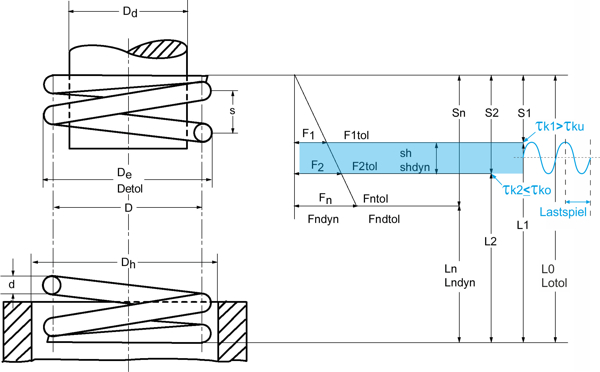
Description Symbole de formule Ressorts de compression [PDF]
Pour les ressorts de compression chargés dynamiquement, la contrainte de cisaillement corrigée s’applique en raison de l’augmentation de contrainte qui en résulte. Avec le facteur de correction de tension k, qui dépend du rapport d’enroulement (rapport du diamètre moyen à l’épaisseur du fil) du ressort, la tension la plus élevée peut être approximativement déterminée.
Contrainte de cisaillement corrigée :
τk1 = k · τ1< τko
τk2 = k · τ2< τko
où k s’applique (selon Bergsträsser)
\Large k=\frac{\frac{D}{d}+0,5}{\frac{D}{d}-0,75}
La contrainte supérieure admissible τko pour chaque type de matériau de ressort est lue à partir du diagramme de résistance à la fatigue (diagramme Goodman) de la norme DIN EN 13906-1 (Fig.12 à Fig.22).
La course de travail souhaitée ne doit pas dépasser la résistance à la fatigue (τkh):
τkh = τk2 – τk1< τkhzul
Avec le Programme de calcul de ressorts Gutekunst WinFSB chaque ressort de compression calculé peut également être calculé pour l’application dynamique. Il ne vous reste plus qu’à activer les options « permanent » et « grenaillé ». Les valeurs dynamiques et le diagramme de Goodman sont alors affichés sous la zone « Stress ».
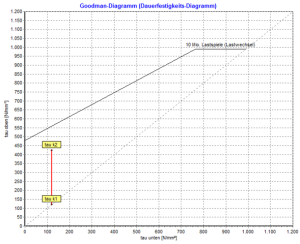
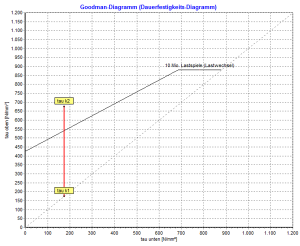
Important!
La contrainte de blocage τczul doit également être vérifiée afin de prendre en compte la superposition de contraintes due aux vibrations naturelles du corps du ressort avec des ressorts de compression chargés dynamiquement.
Les ressorts de compression soumis à une contrainte dynamique doivent être grenaillés avant utilisation. Le grenaillage comprime les couches de surface de manière à obtenir une résistance à la fatigue nettement meilleure.
Pour la résistance à la fatigue d’un ressort de compression, les ressorts normaux sont particulièrement adaptés aux applications moyennement dynamiques Fil d’acier à ressort EN 10270-1DH et SH, ainsi que les fils de ressort de soupape EN 10270-2-VDC, -VDSiCr et -VDCrV pour les applications à haute dynamique.
Une fois la corrosion ou le frottement à travers Mandrin ou manchon agit sur le ressort de compression, la résistance à la fatigue n’est plus garantie!
Information additionnelle: