A lei de Hooke descreve a deformação elástica dos sólidos em um caso especial linear da lei da elasticidade. No processo, a força elástica do corpo muda à medida que este se expande ou se contrai. Quando se utilizam molas de compressão, molas de extensão e molas de torção com desenho cilíndrico, existe uma relação linear entre extensão e força. Este comportamento linear-elástico dos sólidos é chamado de lei de Hooke, cujo nome vem do erudito inglês Robert Hooke.
Através de um desenho diferente – por exemplo, alterando o diâmetro da bobina ou o espaçamento entre bobinas – molas metálicas também podem ser produzidas com uma deformação não linear, ou com uma relação força-deslocamento. Basicamente, a lei de Hooke descreve a tarefa de uma mola metálica: Quanto maior a distância “s” pela qual uma mola metálica é esticada ou comprimida, mais forte é a força contrária “F” da mola. As deformações como na borracha, ou a deformação plástica nas molas metálicas após exceder o limite de proporcionalidade “Rp” não pertencem ao caso especial linear da lei da elasticidade.
Table of Contents
Fórmula Hooke’s law Molas metálicas
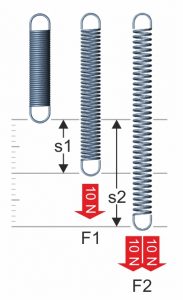
A lei de Hooke diz que a viagem da mola “s” depende linearmente da força de atuação “F”.
A lei da Fórmula Hooke:
Na fórmula da lei de Hooke, a constante de mola “R” serve como fator de proporcionalidade e descreve a rigidez da mola metálica. No caso de uma mola de tensão, o comportamento linear é mostrado quando carregada com um peso. Depois de duplicar o peso, o duplo caminho “s” também ocorre.
Esta propriedade é importante, por exemplo, para a aplicação de molas metálicas como armazenamento de força, restauração de força, distribuição de carga e em conexões de travamento de força. Para outros materiais – como a borracha – a relação entre a força aplicada e a expansão não é linear.
A constante da mola
A constante da mola ou taxa de mola “R” depende do material e do desenho da mola. Com uma força crescente ou um enrolamento mais apertado do fio utilizado, a mola constante de uma mola helicoidal aumenta. É dado na unidade Newton por milímetro (N/mm) e é o quociente entre a força da mola “F” e o curso da mola “s”:
Aplica-se o seguinte:
F = Força da mola [N]
R = taxa de mola / constante de mola [N/mm]
s = deflexão da mola [mm]
Cálculo da força da mola:
A força da mola pode ser calculada com a seguinte fórmula:
Aplica-se o seguinte:
F = Força da mola [N] R = Taxa da mola / constante da mola [N/mm] s = Curso da mola [mm]
Porque é que a mola é sempre negativa? O sinal menos na equação significa que – em relação à posição de descanso – a direção de deflexão de uma mola é oposta à força da mola.
A fórmula para a força das molas não é usada apenas para molas de compressão, molas de extensão e de torção, mas também para outros corpos elásticos. A força da mola é, portanto, um tópico importante na mecânica e na tecnologia de materiais, entre outros.
Se necessário em
Compressão-
,
Tensão
ou
Molas de torção
Basta enviar-nos os dados para a mola metálica necessária em verkauf@gutekunst-co.com, indicando o número de peças e o desenho. Faremos uma oferta não vinculativa em cima da hora. Para mais informações, contacte o nosso departamento técnico directamente pelo telefone (+49) 035877 227-13.
Para mais informações:
Tipos de tensão Molas de compressão
Tipos de molas de tensão Tensão
Calcular a taxa de molas para molas cilíndricas
Loja de Primavera Gutekunst Federn