Hookeův zákon popisuje elastický deformace z Pevné látky v lineárním zvláštním případě zákona pružnosti. Elastická síla těla se mění s expanzí nebo kompresí. Při použití Tlačné pružiny , Tažné pružiny a Torzní pružiny S válcový design existuje a lineární vztah mezi expanzí a silou . Toto lineárně-elastické chování pevných látek se nazývá Hookeův zákon, pojmenovaný podle anglického učence Roberta Hooke.
Může se použít jiný design – například změněný průměr cívky nebo rozteč cívky Kovové pružiny také s nelineární deformací nebo Poměr síly a dráhy vyrobit. Hookův zákon v zásadě popisuje úkol kovové pružiny: Čím delší je vzdálenost „s“, o kterou je kovová pružina natažena nebo stlačena, tím silnější je působící síla pružiny „F“ pružiny. Deformace jako v gumě nebo plastické deformace v kovových pružinách po překročení Limit proporcionality „Rp“ nepatří do lineárního zvláštního případu zákona pružnosti.
Table of Contents
Kovové pružiny Formule Hooke’s Law
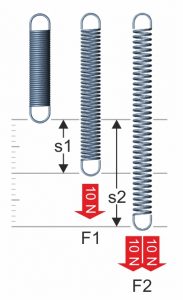
Hookův zákon říká, že průhyb pružiny „s“ závisí lineárně na síle „F“.
Hookův vzorec: R=\frac{F}{s}
Ve vzorci Hookova zákona slouží konstanta pružiny „R“ jako faktor úměrnosti a popisuje tuhost kovové pružiny. Tažná pružina ukazuje lineární chování při zatížení závaží. Po zdvojnásobení hmotnosti dojde také k dvojité dráze „s“.
Tato vlastnost je zásadní například pro použití kovových pružin jako akumulace energie, obnovení síly, rozložení zatížení a pro ne-pozitivní spojení. U jiných materiálů – například gumy – není vztah mezi silou a roztažením lineární.
Jarní konstanta
The Konstanta pružiny nebo tuhost pružiny„R“ závisí na materiálu a Návrh pružiny. Se zvyšující se pevností nebo pevnějším navíjením použitého drátu se zvyšuje pružinová konstanta spirálové pružiny. Udává se v jednotkách Newton na milimetr (N / mm) a je podílem síly pružiny „F“ a výchylky pružiny „s“:
R=\frac{F}{s}
Platí následující:
F = síla pružiny [N]
R = rychlost pružiny / konstanta pružiny [N/mm]
s = zdvih pružiny [mm]
Výpočet síly pružiny:
Sílu pružiny lze vypočítat podle následujícího vzorce:
F = -R\cdot s
Platí následující:
F = síla pružiny [N]; R = tuhost pružiny / konstanta pružiny [N/mm]; s = dráha pružiny [mm]
Proč?Konstanta pružiny záporný? Znaménko mínus v rovnici znamená, že – ve vztahu k klidové poloze – je směr vychýlení pružiny opačný k síle pružiny.
Vzorec pro sílu pružiny není jen na Tlačné pružiny , Tažné pružiny a Zkrutné pružinypoužité, ale také pro další elastická těla. Síla pružiny je proto důležitým tématem v mechanice a technologii materiálů.
V případě potřeby Tlačné pružiny , Tažné pružiny nebo Torzní pružiny stačí nám poslat na order@gutekunst-co.com údaje o požadované kovové pružině s podrobnostmi o počtu kusů a výkresem. V krátké době vám dáme nezávaznou nabídku. Další informace získáte přímo na našem technickém oddělení service@gutekunst-co.com.
Dodatečné informace:
Vypočítejte rychlost pružení pro válcové pružiny
Obchod s pružinami v obchodě Gutekunst Federn