Hookesche’s law describes the elastic deformation of solids in a linear special case of the Elasticity Act. In this process, the elastic force of the body changes with stretching or squeezing. When applying compression springs, extension springs and torsion springs with a cylindrical design, there is a linear relationship between expansion and force. This linear-elastic behavior of solids is called Hookese’s Law, named after the English scholar Robert Hooke.
By a different design – as by a changed winding diameter or winding distance – metal springs can also be produced with a non-linear deformation, or force-way ratio. Basically, Hookese’s law describes the task of a metal spring: The longer the distance “s” is, around which a metal spring is stretched or compressed, the stronger the counteracting spring force “F” of the spring. Deformations as in the case of rubber, or plastic deformation in metal springs after exceeding the proportionality limit “Rp” do not belong to the special linear case of the Law of Elasticity.
Table of Contents
Formula Hookese’s Law Metal Springs
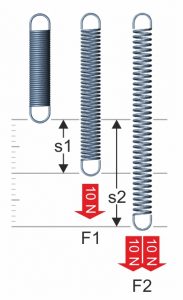
Hooke’s law states that the spring travel “s” depends linearly on the acting force “F”.
Hooke’s law formula: R=\frac{F}{s}
In the formula of Hooke’s law, the spring constant “R” serves as a proportionality factor and describes the stiffness of the metal spring. With a tension spring, the linear behavior is shown when loaded with a weight. After doubling the weight, the double path “s” also occurs.
This property is important, for example, for the application of metal springs as a force storage, resetting force, load distribution and for force-locking connections. For other materials, such as rubber, the relationship between acting force and expansion is not linear.
The spring rate
The spring constant or spring rate “R” depends on the material and the design of the spring. With increasing thickness or tighter winding of the wire used, the spring constant of a coil spring increases. It is given in the unit Newton per millimeter (N/mm) and is the quotient of the spring force “F” and the travel “s”:
R=\frac{F}{s}
The following applies:
F = Spring Force [N]
R = Spring rate / Spring constant [N/mm]
s = spring deflection [mm]
Calculation of spring force:
The spring force can be calculated using the following formula:
F=-R\cdot s
The following applies:
F = spring force [N]; R = spring rate / spring constant [N/mm]; s = spring travel [mm]
Why is the spring rate negative? The minus sign in the equation means that, relative to the resting position, the direction of deflection of a spring is opposite to the spring force.
The spring force formula is used not only for Compression springs,Extension springs and Torsion springs, but also for other elastic bodies. An important topic is therefore spring force in mechanics and materials technology, among other things.
If you need pressure, extension or torsion springs, simply send us the data of the required metal spring with indication of the number of pieces and the drawing under service@gutekunst-co.com. We will prepare a non-binding offer for you at short notice. For more information, please contact our technical department directly on (+49) 035877 2270.
For more information:
Types of stress compression springs
Types of stress extension springs
Ball blasting of metal springs
Calculate spring rate for cylindrical springs
Spring shop by Gutekunst Federn