Před interpretací Kompresní pružina V zásadě by mělo být objasněno, zda je zamýšlený typ napětí statický, kvazi-statický nebo dynamický.

Statické nebo kvazistatické napětí

Časově konstantní (klidové) zatížení nebo časově proměnlivé zatížení s celkovým menším než 10 000 zdvihy nebo malými zdvihovými napětími až 0,1 x únavová pevnost (τkh = τk2 -τk1).

Dynamický stres

Dynamické napětí v pružinách je definováno jako napětí, které se v průběhu času mění s více než 10 000 změnami zatížení nebo tahová napětí přes 0,1 x únavová pevnost (τkh) s konstantním a proměnným tahovým napětím. Pružina je většinou předpjatá a vystavena periodickým bobtnáním se sinusovou křivkou, které se vyskytují náhodně (stochasticky), jako je tomu v případě zavěšení vozidla.

V závislosti na požadovaném počtu zatěžovacích cyklů „N“ bez přerušení se rozlišuje:

1. Oblast Únavová síla s počtem zatěžovacích cyklů
N ≥ 10 7. pro pružiny tvarované za studena
N ≥ 2 x 10 6. pro pružiny tvarované za tepla
S napětím zdvihu menším než únavová pevnost.

2. Oblast Únavová síla s počtem zatěžovacích cyklů
N< 10 7. pro pružiny tvarované za studena
N< 2 x 10 6. pro pružiny tvarované za tepla
S napětím zdvihu vyšším než únavová pevnost a menším než časovým napětím

Stávající smykové napětí se stanoví následovně.

Smykové napětí od síly: \tau=\frac<wpml_curved wpml_value='8DF'></wpml_curved>{\pi d^<wpml_curved wpml_value='3'></wpml_curved>}

Smykové napětí z dráhy: \tau=\frac<wpml_curved wpml_value='Gds'></wpml_curved>{\pi nD^<wpml_curved wpml_value='2'></wpml_curved>}

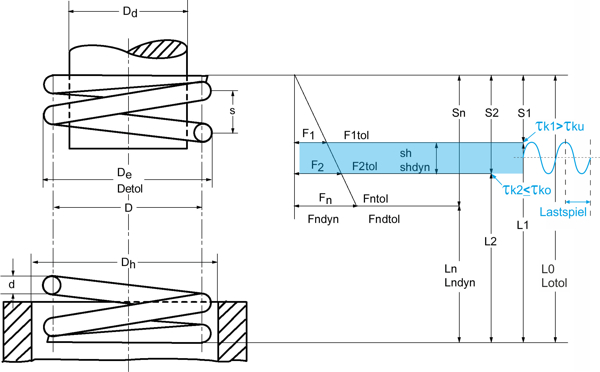
Vibrační diagram dynamická tlaková pružina
Vibrační diagram dynamická tlaková pružina

Popis Symbol vzorec tlačné pružiny

U dynamicky zatížených tlačných pružin se použije opravené smykové napětí z důvodu výsledného zvýšení napětí. S korekčním faktorem napětí k, který závisí na poměru navíjení (poměr středního průměru k tloušťce drátu) pružiny, lze přibližně určit nejvyšší napětí.

Opravené smykové napětí :

τk1 = k · τ1< τko

τk2 = k τ2< τko

kde platí pro k (podle Bergsträssera)

k=\frac{\frac<wpml_curved wpml_value='D'></wpml_curved><wpml_curved wpml_value='d'></wpml_curved>+0,5}{\frac<wpml_curved wpml_value='D'></wpml_curved><wpml_curved wpml_value='d'></wpml_curved>-0,75}

Povolené horní napětí τko pro každý typ pružinového materiálu se čte z diagramu únavové pevnosti (Goodmanův diagram) z DIN EN 13906-1 (obr. 12 až obr. 22).

Požadovaný pracovní zdvih nesmí překročit mez únavy (τkh):

τkh = τk2 – τk1< τkhzul

S Program výpočtu pružin Gutekunst WinFSB každou vypočítanou tlačnou pružinu lze vypočítat také pro dynamickou aplikaci. Jediné, co musíte udělat, je aktivovat možnost „permanent“ a „shot peened“. Dynamické hodnoty a Goodmanův diagram se poté zobrazí v oblasti „Napětí“.

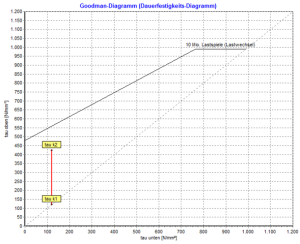
Grafické WinFSB trvalé
Goodmanův diagram WinFSB odolný
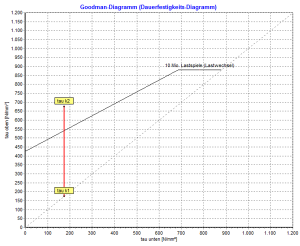
Grafika WinFSB není trvalá
Goodmanův diagram není trvalý

 

 

 

 

 

 

 

 

Důležité!

Rovněž je třeba zkontrolovat blokové napětí τczul, aby se zohlednilo superpozice napětí v důsledku přirozených vibrací tělesa pružiny s dynamicky zatíženými tlačnými pružinami.

Dynamicky namáhané tlačné pružiny by měly být před použitím brokovány. Shot peening komprimuje povrchové vrstvy tak, aby bylo dosaženo výrazně lepší únavové pevnosti.

Pro únavovou pevnost tlačné pružiny jsou normální vhodné zejména pro středně dynamické aplikace Pružinový ocelový drát EN 10270-1DH a SH, stejně jako vodiče ventilové pružiny EN 10270-2-VDC, -VDSiCr a -VDCrV pro vysoce dynamické aplikace.

Jakmile dojde ke korozi nebo tření Trn nebo rukáv působí na tlačnou pružinu, únavová pevnost již není zaručena!

 

Dodatečné informace:

Druhy zatížení tlačných pružin
Štítky: