Pružinová konstanta popisuje při Tlačné pružiny , Tažné pružiny a Torzné (skrutné) pružiny zvýšení síly ve vztahu k Odpružení , nebo s torzními pružinami ve vztahu k úhlu otáčení. Také se tomu říká Jarní sazba , Tvrdost pružiny nebo tuhost pružiny a definuje tvrdost pružiny. S Jarní charakteristika je ukázán průběh pružinové konstanty. Je pružinová konstanta lineární, tj Síla pružiny rovnoměrně roste se zatížením pružiny, pak je charakteristika pružiny přímá (b.). Pokud se naopak síla pružiny zvětšuje neúměrně nebo neúměrně s rostoucím zatížením, pak hovoříme o progresivní (a.) Nebo degresivní (c.) Pružinové charakteristice. Konstanta pružiny pro tlačné a tažné pružiny je uvedena v jednotce Newton / milimetr a pro torzní pružiny jako krouticí moment pružiny v Newton milimetrech.
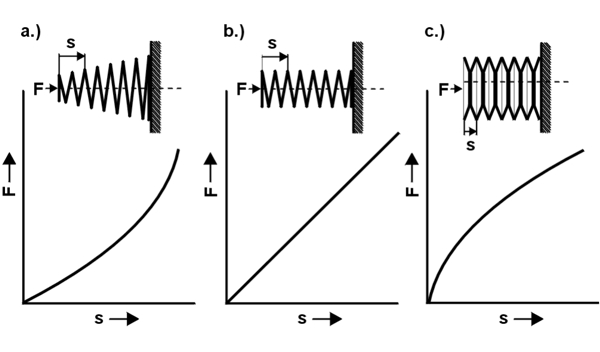
Pro pružinovou konstantu s přímou charakteristikou pružiny tedy platí:
Tlakové a tažné pružiny
R = \frac{F2-F1}{s2-s1}
Torzné (skrutné) pružiny
R = \frac{M2-M1}{\alpha2-\alpha1}
Vzorce pro výpočet konstanty pružiny pro tlačné pružiny, tažné pružiny a torzní pružiny:
Formule pružinové konstantní tlačné pružiny (N / mm) ( Tlakové pružiny kolekce Formula )
R=\frac{Gd^{4}}{8D^{3}n}
Formule pružiny konstantní tažné pružiny (N / mm) ( Prodlužovací pružiny kolekce Formula )
R=\frac{Gd^{4}}{8D^{3}n}=\frac{F-F0}{s}
Formule pružiny krouticí moment nohou (Nmm) ( Kolekce formulí pružiny nohou )
R_{M}=\frac{M}{\alpha}=\frac{d^{4}E}{3667Dn}
Vysvětlení vzorce:
α = úhel otočení (°)
d = průměr drátu (mm)
D = střední průměr cívky (mm)
E = modul pružnosti (N / mm²) ( E-modul různých pružinových ocelí )
F = síla pružiny (N)
G = kluzný a smykový modul (N / mm²) ( G-modul vyrobený z různých pružinových ocelí )
F0 = vnitřní síla předpětí
M = točivý moment (Nmm)
n = počet pružných cívek (kusů)
R = pružinová konstanta (N / mm)
RM = krouticí moment pružiny (Nmm)
s = zdvih pružiny (mm)
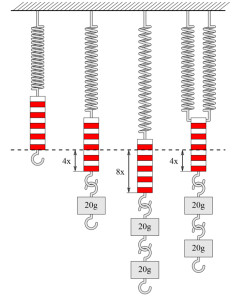
Pružinovou konstantu lze také určit pomocí zkoušky tahem. Pružina je odtržena silou (F) a vychýlením pružiny / Jarní práce (s2) změřeno. To dává pružinovou konstantu v Newtonech / milimetr.
R = \frac{F}{s}
Tato zkouška tahem by však měla být provedena s různými silami, aby se získal přesný výsledek měření.
Další informace