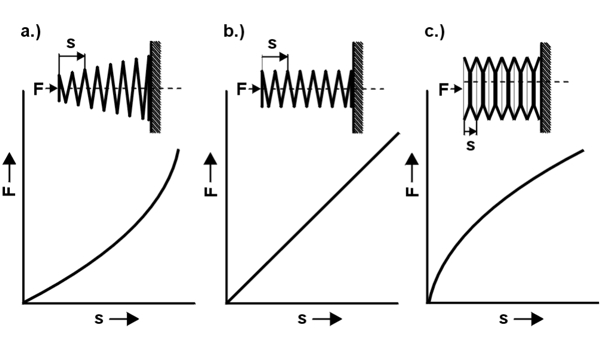
The spring constant describes at Compression springs , Tension springs and Torsion springs the increase in force in relation to the Suspension travel , or with torsion springs in relation to the angle of rotation. It is also called Spring rate , Spring hardness or spring stiffness and defines the hardness of a spring. With the Spring characteristic the course of a spring constant is shown. Is the spring constant linear, ie the Spring force increases evenly with the load on the spring, then the spring characteristic is straight (b.). If, on the other hand, the spring force increases disproportionately or disproportionately with increasing load, then we speak of a progressive (a.) Or degressive (c.) Spring characteristic. The spring constant for compression springs and tension springs is specified in the unit Newton / millimeter and for torsion springs as the spring torque rate in Newton millimeters.
The following therefore applies to the spring constant with a straight spring characteristic:
Compression and tension springs
R = \frac{F2-F1}{s2-s1}
Schenkelfedern
R = \frac{M2-M1}{\alpha2-\alpha1}
Formulas for calculating the spring constant for compression springs, tension springs and torsion springs:
Formula spring constant compression springs (N / mm) ( Formula collection compression springs )
R=\frac{Gd^{4}}{8D^{3}n}
Formula spring constant tension springs (N / mm) ( Formula collection extension springs )
R=\frac{Gd^{4}}{8D^{3}n}=\frac{F-F0}{s}
Formula spring torque rate leg springs (Nmm) ( Torsion springs formula collection )
R_{M}=\frac{M}{\alpha}=\frac{d^{4}E}{3667Dn}
Formula explanation:
α = angle of rotation (°)
d = wire diameter (mm)
D = mean coil diameter (mm)
E = modulus of elasticity (N / mm²) ( E-modulus of different spring steels )
F = spring force (N)
G = sliding and shear modulus (N / mm²) ( G-module made from different spring steels )
F0 = internal preload force
M = torque (Nmm)
n = number of resilient coils (pieces)
R = spring constant (N / mm)
RM = spring torque rate (Nmm)
s = spring deflection (mm)
The spring constant can also be determined by means of a tensile test. The spring is pulled apart with a force (F) and the spring deflection / Spring work (s2) measured. This gives the spring constant in Newtons / millimeter.
R = \frac{F}{s}
However, this tensile test should be made with different forces in order to obtain an accurate measurement result.
Further information