Design de molas metálicas – Parte 1 “Noções básicas › Gutekunst Federn › Cálculo da mola, Construção, Design de mola, Druckfedern, Molas de torção, Noções básicas, Schenkelfedern, Zugfedern

Abaixo você pode ler o resumo do básico para o projeto de molas de compressão, molas de extensão e molas de torção.

As molas técnicas são ainda hoje um dos elementos de máquinas mais importantes e são utilizadas com sucesso em veículos, aparelhos mecânicos ou electrotécnicos de precisão, equipamentos médicos, aparelhos domésticos e muito mais. Muitas vezes a função de todo o aparelho ou parte da máquina depende do funcionamento sem problemas da mola metálica.

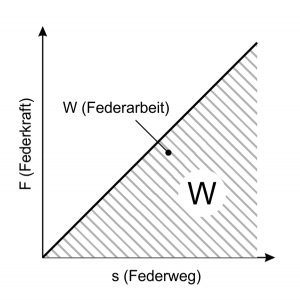
Molas metálicas são elementos que se deformam especificamente sob carga e retornam à sua forma original quando a carga é removida. No processo, a energia fornecida é convertida em trabalho de mola (W) e liberada novamente em um momento posterior (armazenamento de força). No entanto, as molas metálicas só executam de forma fiável esta deformação e absorção de energia dentro dos limites concebidos para o efeito. Portanto, o projeto correto da mola e o cálculo da mola é um componente importante para o perfeito funcionamento da mola metálica.

A curva característica da mola

Molas metálicas ou molas técnicas são julgadas de acordo com as suas características de mola. Esta curva característica da mola representa a dependência da força da mola (F) no curso da mola (s). Dependendo da característica da mola necessária (linear, progressiva, degressiva ou combinada), a forma e o tipo de mola também mudam.

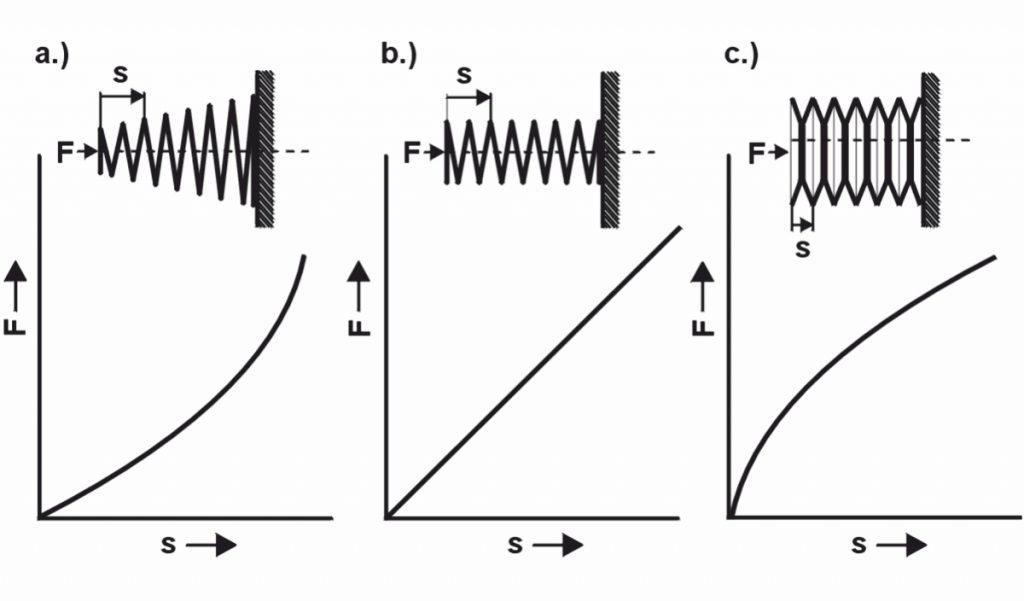
Características da mola - Gutekunst Federn — Características da primavera a) Progressivo de uma mola de compressão cónica, b) linear de uma mola de compressão cilíndrica, degressiva de uma coluna de mola de disco

A taxa da mola (R) determina a curva característica da mola no diagrama da mola. A taxa de mola (R) é, portanto, um valor importante no projeto da mola apropriada. Com uma característica de mola linear, a taxa de mola é constante. Molas com uma característica de mola curva têm uma taxa de mola variável. As seguintes fórmulas aplicam-se, portanto, a uma curva característica linear:

para molas de compressão e extensão

$R=\frac{F2-F1}{s2-s1}$

para pernas e molas de torção

$R_{M}=\frac{M2-M1}{\alpha2-alpha1}$

O trabalho da Primavera

Ao tensão da mola metálica, o trabalho é feito, que é libertado novamente quando relaxa. O trabalho de mola (W) resulta sempre como uma superfície abaixo da característica da mola. Com uma curva característica de mola linear, aplica-se portanto o seguinte:

para molas de compressão e extensão

$W=\frac{1}{2}F\cdot s$

para molas de torção

$W=\frac{1}{2}M=cdot =alpha$

Calculando o valor da utilidade de volume, diferentes tipos de molas podem ser determinados através da relação entre a energia da mola e a energia da mola. (W) e espaço de instalação (V) um com o outro:

$\{A}==frac{W}{V}$

A histerese

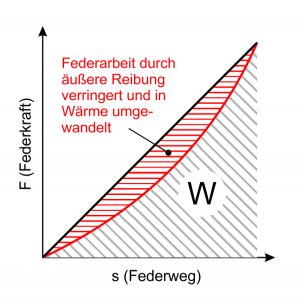
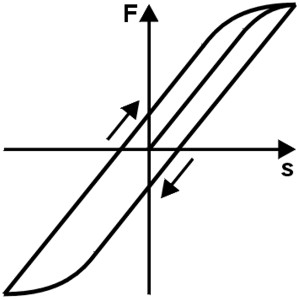
O comportamento da suspensão pode ser influenciado por fricção externa. Estas forças friccionais impedem a mola de se deformar para trás. No caso de tensão alternada, esta manifesta-se sob a forma de um ciclo de histerese. Parte do trabalho da mola é convertida em calor por fricção e depois é “perdida”. Uma vez que isto é indesejável quando se utilizam molas, qualquer fricção deve ser evitada construtivamente através da disposição e desenho das molas.

Molas de aço de ciclo de histerese — Ciclo de histerese relacionado com fricção

O relaxamento

Por exemplo, se uma mola de compressão é comprimida a um determinado comprimento entre placas paralelas a uma temperatura mais elevada, pode-se ver que a força da mola diminui gradualmente ao longo do tempo. Esta perda de força aumenta com o aumento da temperatura e da tensão.

Orelaxamento do material é uma deformação plástica que se manifesta como uma perda de força a um comprimento de instalação constante. Isto é dado como uma percentagem em relação à força inicial F1:

$Relaxamento=frac{\frac{\delta F\cdot 100}{F1}$

O diagrama seguinte mostra o curso básico do relaxamento e a velocidade do relaxamento:

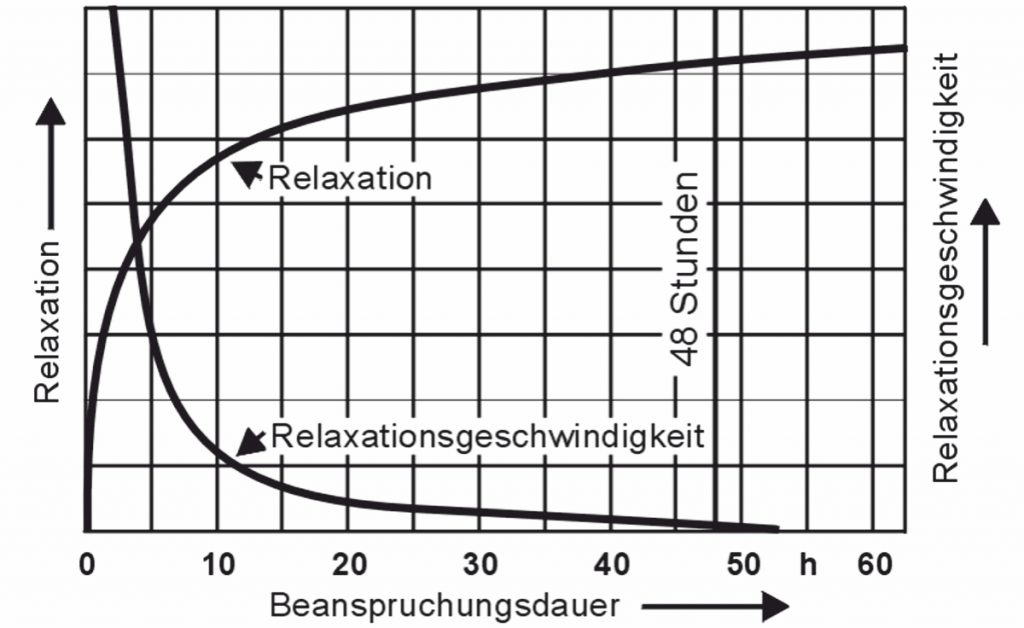
Gráfico de Relaxamento - Gutekunst Federn — Curso do tempo de relaxamento e velocidade de relaxamento para molas de compressão helicoidais

Os valores de relaxamento após 48 horas são considerados como valores característicos, embora o relaxamento ainda não esteja completamente terminado neste ponto. A EN 13906-1 contém diagramas de relaxamento dependentes do material. Estes só devem ser incluídos pelo projectista se forem colocadas elevadas exigências à constância da força da mola. O relaxamento em diferentes condições de temperatura é mostrado no cálculo do programa WinFSB do Gutekunst Federn, disponível em www.federnshop.comtambém é mostrado.

A escolha certa do material

Asmolas metálicas devem ser feitas de um material adequado e concebidas e construídas de tal forma que retornem à sua forma original após a remoção de uma carga aplicada. Esta propriedade é expressa no módulo de elasticidade e no módulo de deslizamento. Estes parâmetros materiais expressam a relação entre tensão e deformação e devem ter um valor tão alto quanto possível.

Além disso, materiais de mola:

têm altos limites elásticos, ou seja, uma grande faixa puramente elástica,
suportar as tensões correspondentes mesmo a temperaturas elevadas sem grande perda de força (baixo relaxamento),
têm uma elevada resistência à fadiga (estrutura de grão fino, livre de impurezas),
têm capacidade de deformação suficiente,
têm uma superfície que é o mais escorregadia possível,
resistir a certos requisitos de protecção anticorrosiva,
ser eletricamente condutivo ou não magnético.

Elasticidade e módulos deslizantes de diferentes materiais

material	módulo de elasticidade [N/mm²]	Módulo G [N/mm²]
Fio de aço de mola extraído patenteado de acordo com a EN 10270-1	206000	81500
Fio de mola de válvula saciada de óleo de acordo com a EN 10270-2	206000	81500
Aço laminado a quente de acordo com a EN10089	206000	78500
Fita laminada a frio de acordo com a norma EN 10132	206000	78500
X10 CrNi 18 8 (1.4310)	185000	70000
X7 CrNiAl 17 7 (1.4568)	195000	73000
X5 CrNiMo 17-12-2 (1.4401)	180000	68000
CuSn6 R950 de acordo com a EN 12166	115000	42000
CuZn36 R700 de acordo com a EN 12166	110000	39000
CuBe2 de acordo com a norma EN 12166	120000	47000
CuNi18Zn20 de acordo com a EN 12166	135000	45000
CuCo2Be segundo a norma EN 12166	130000	48000
Inconel X750	213000	76000
Nimonic 90	213000	83000
Hastelloy C4	210000	76000
Liga de titânio TiAl6V4	104000	39000

Influência da temperatura de trabalho na seleção dos materiais

Comportamento a temperaturas de trabalho elevadas

O nível da temperatura de trabalho pode influenciar significativamente o funcionamento de uma mola, já que a tendência para relaxar aumenta com o aumento da temperatura. Após a avaliação dos diagramas de relaxamento, as seguintes temperaturas limite podem ser assumidas para os materiais de mola mais importantes.

Limitar as temperaturas dos materiais primaveris ao mínimo de relaxamento

material	Temperatura máxima de trabalho em °C a
	elevada carga	Carga baixa
Fio de aço de mola extraído patenteado de acordo com a EN 10270-1	60-80	80-150
Fio de mola de válvula saciada de óleo de acordo com a EN 10270-2	80-160	120-160
X10CrNi 18.8 (1.4310)	160	250
X7CrNiAl 17.7 (1.4568)	200	350
X5CrNiMo 17-12-2 (1,4401)	160	300
Rio CuSn6	80	100
CuZn36	40	60
CuBe2	80	120
CuNi18Zn20	80	120
Inconel X750	475	550
Nimonic90	500	500

Além disso, as propriedades dos materiais do módulo de elasticidade e do módulo de cisalhamento, que são importantes para a função da mola, diminuem com o aumento da temperatura. Tanto o módulo de cisalhamento como o módulo de elasticidade são determinados a temperaturas mais elevadas de acordo com a seguinte fórmula, utilizando como base as características do material à temperatura ambiente (20°C).

$G_{t}=G_{20}=\frac{3620-T}{3600}$

resp.

$E_{t}=E_{20}=\frac{3620-T}{3600}$

Isto permite ao projetista determinar as forças reais da mola à temperatura de operação prevista.

Comportamento a baixas temperaturas de funcionamento

Quando utilizado em sistemas de refrigeração, no espaço ou no frio rigoroso do inverno, temperaturas tão baixas quanto – 200 ° devem, às vezes, ser suportadas. Apesar da crescente resistência à tração, as baixas temperaturas têm um efeito desfavorável, pois a tenacidade dos materiais diminui e podem ocorrer fraturas frágeis. Aços para molas inoxidáveis, bem como ligas de cobre e níquel, são preferíveis aos fios para molas patenteados e aos fios para molas de válvulas para aplicações a baixa temperatura. A tabela seguinte mostra as temperaturas limite.

Recomendações para uso a baixa temperatura

material	Temperatura mínima de trabalho em °C
Fio de aço de mola extraído patenteado de acordo com a EN 10270-1	-60
Fio de mola de válvula saciada de óleo de acordo com a EN 10270-2	-60
X10CrNi 18.8 (1.4310)	-200
X7CrNiAl 17.7 (1.4568)	-200
X5CrNiMo 17-12-2 (1,4401)	-200
Rio CuSn6	-200
CuZn36	-200
CuBe2	-200
CuNi18Zn20	-200
Inconel X750	-100
Nimonic90	-100

Use sistemas de molas

Por razões de design, também é possível utilizar várias molas para absorver forças e movimentos. Os sistemas de molas simples são circuitos paralelos e circuitos.

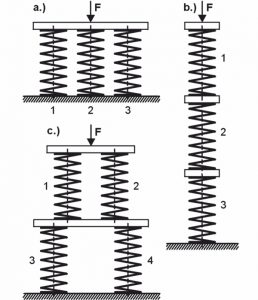
Gráfico de Sistemas de Molas - Gutekunst Federn — Sistemas de primavera a) Ligação paralela, b) Ligação em série, c) Circuito misto

a) Ligação paralela

As molas estão dispostas de tal forma que a carga externa (F) é distribuída proporcionalmente entre as molas individuais, mas o curso das molas individuais é o mesmo. Isto resulta em:

$s=s1=s2=s3=s3=...$ (total de viagens de primavera)

$F=F1+F2+F3+...$ (força total da mola)

$R=R1+R2+R3+...$ (taxa total da Primavera)

A taxa de molas do sistema global de um circuito paralelo é sempre maior do que a taxa de molas das molas individuais

b) Ligação em série

As molas estão dispostas uma atrás da outra para que a mesma força actue em cada mola, mas o percurso da mola é dividido entre as molas individuais. Resulta:

$s=s1+s2+s3+...$ (total de viagens de primavera)

$F=F1=F2=F3=F3=...$ (força total da mola)

$R=\frac{1}{\frac{1}{R1}+\frac{1}{R2}+\frac{1}{R3}+...}$ (taxa total da Primavera)

A taxa de molas do sistema global de uma conexão em série é sempre menor do que a taxa de molas das molas individuais

c) Circuito misto

Várias molas são ligadas em paralelo e em série. Devido ao equilíbrio, R1=R2 e R3=R4 devem ser. Para o caso apresentado:

$R=\frac{1}{\frac{1}{R1+R2}+\frac{1}{R3+R4}+...}$ (taxa total da Primavera)

A taxa de molas do sistema global do circuito misto mostrado está entre a menor e a maior taxa de molas das molas individuais!

Na segunda parte da série de informação“Desenho de molas metálicas – Parte 2 “Cálculo” apresentamos os parâmetros de cálculo para a verificação funcional e de resistência das molas de compressão, molas de extensão e molas de torção.

Se precisar de um desenho individual de mola, basta enviar-nos os dados chave da mola metálica necessária para technik@gutekunst-co.com, contactar o nosso departamento técnico pelo telefone (+49) 035877 227-11 ou utilizar o programa de cálculo de molas Gutekunst WinFSB em www.federnshop.com para cálculo gratuito de molas de compressão, molas de extensão e molas de torção.

Para mais informações: