Das Elastizitätsmodul ist ein Materialkennwert aus der Werkstofftechnik und definiert die Steigung des Graphen im Spannungs-Dehnungs-Diagramm. Dieser Kennwert beschreibt den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers in einem linear-elastischem Verhalten. Der Elastizitätsmodul ist unter den Abkürzungen E-Modul oder als Formelzeichen E in der Federnberechnung bekannt; er hat die Einheit „N/mm²“ einer mechanischen Spannung.
Je mehr Widerstand ein Material seiner elastischen Verformung entgegensetzt, umso größer ist der Betrag des Elastizitätsmoduls. Ein Bauteil aus einem Material mit hohem Elastizitätsmodul (beispielsweise Federstahl) ist somit steifer als ein Bauteil gleicher Konstruktion (mit identischen geometrischen Abmessungen), das aus einem Material mit niedrigem Elastizitätsmodul (beispielsweise Gummi) besteht. Dabei ist der Elastizitätsmodul die Proportionalitätskonstante in Hookesches Gesetz.
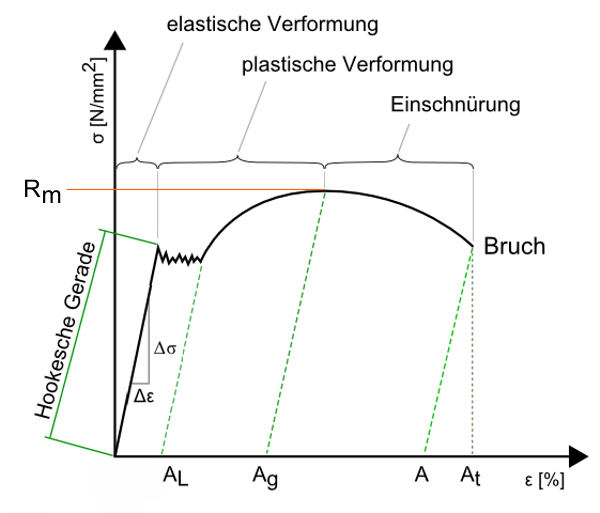
Rm = Zugfestigkeit
σ = Spannung
AL = Lüdersdehnung
Ag = Gleichmaßdehnung
A = Bruchdehnung
At = gesamte Dehnung bei Bruch
Ɛ = Dehnung
Die Definition des Elastizitätsmoduls: Der Elastizitätsmodul ist die Steigung des Graphen im Spannungs-Dehnungs-Diagramm bei einachsiger Belastung innerhalb des linearen Elastizitätsbereichs. Dieser lineare Bereich heißt auch Hookesche Gerade.
Dabei bezeichnet
σ = F/A (=Kraft/Fläche) die mechanische Spannung (Normalspannung, nicht Schubspannung) und Ɛ = ∆L/L0 die Dehnung. Die Dehnung ist das Verhältnis von Längenänderung ∆L = L – L0 zur ursprünglichen Länge L0
E – Elastizitätsmodul
σ – Spannung
ε – Dehnung
Hier gibt es das Elastizitätsmodul zur Federnberechnung bei Raumtemperatur (20°C) für die wichtigsten Federwerkstoffe.
Der Elastizitätsmodul ist aber nicht bezüglich aller physikalischen Größen konstant. So beeinflussen zudem die unterschiedlichen Umgebungseinflüsse, wie zum Beispiel Temperatur oder Feuchte, den E-Modul. Die Anpassung des Elastizitätsmoduls wird bei höheren Temperaturen nach folgender Formel ermittelt, wobei die Federwerkstoffkennwerte bei Raumtemperatur (20°C) als Basis dienen.
Für die Auslegung einer passenden Druck-, Zug- oder Schenkelfeder wenden Sie sich bitte direkt an unsere Technikabteilung unter Telefon (+49) 035877 227-13 oder cunewalde@gutekunst-co.com.
Weitere Informationen: