Design of metal springs – Part 1 “Basics” › Gutekunst Federn › Federauslegung, Federberechnung, Grundlagen, Konstruktion, Schenkelfedern, Springs, Tension springs, Torsion springs

Below is the summary of the basics about Spring design of Compression springs , Tension springs and Leg springs .

Technical springs are still one of the most important machine elements today and are used successfully in vehicles, precision mechanical or electrotechnical devices, medical devices, household appliances and much more. The function of the entire device or machine part often depends on the trouble-free operation of the metal spring.

Metal springs are elements that deliberately deform under load and return to their original shape when the load is removed. The energy supplied is in Spring work (W) converted and released again at a later point in time (energy store). However, the metal springs only reliably perform this deformation and energy absorption within the limits designed for this purpose. Therefore is the right one Spring design and Spring calculation an important component for the perfectly working metal spring.

Table of Contents

The spring characteristic curve

Metal springs or technical springs are made according to your Spring characteristic judged. This spring characteristic represents the dependence of the Spring force (F) represents the spring travel (s). Because depending on which spring characteristic is required (linear, progressive, degressive or combined), the shape and type of the spring also change.

Spring characteristics - Gutekunst Federn — Spring characteristics a) progressive of a conical compression spring, b) linear a cylindrical compression spring, degressive a disc spring column

With the Spring rate (R) the spring characteristic is determined in the spring diagram. The spring rate (R) is therefore an important value when designing the spring for the right spring. At linear spring characteristic the spring rate is constant. Springs with a curved spring characteristic have a variable spring rate. The following formulas therefore apply to a linear characteristic:

for compression and tension springs

R=\frac{F2-F1}{s2-s1}

for leg and torsion springs

R_{M}=\frac{M2-M1}{\alpha2-\alpha1}

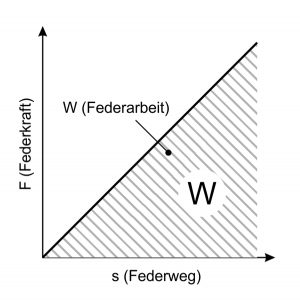
The spring work

When the metal spring is tensioned, work is done, which is then released again when the tension is released. The spring work (W) always results as the area below the spring characteristic. With a linear spring characteristic, the following applies:

for compression and tension springs

W=\frac{1}{2}F\cdot s

for leg and torsion springs

W=\frac{1}{2}M\cdot \alpha

By calculating the volume utility value, different types of springs can be determined using the ratio of spring work (W) and installation space (V) compare with each other:

\eta_{A}=\frac{W}{V}

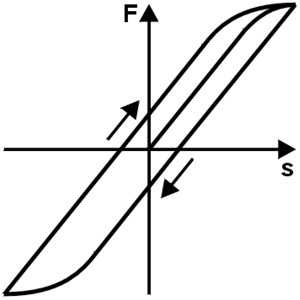
The hysteresis

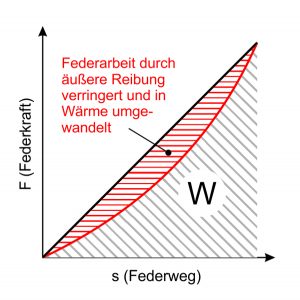
The suspension behavior can be influenced by external friction. These frictional forces hinder the spring’s recovery. In the case of alternating loads, this is expressed in the form of a Hysteresis loop . Part of the spring work is converted into heat by the friction and is then “lost”. Since this is undesirable when using springs, any friction should be designed by arrangement and Shape of feathers be avoided.

Hysteresis loop steel springs — Frictional hysteresis loop

The relaxation

For example, if a compression spring is used higher temperature is compressed to a certain length between parallel plates, one can determine that the Spring force gradually decreases over time. This loss of strength increases with increasing temperature and tension.

Relaxation of the material is a plastic deformation that manifests itself as a loss of force with a constant installation length. This is given as a percentage of the output force F1:

Relaxation=\frac{\Delta F\cdot 100}{F1}

The following diagram shows the basic course of the relaxation and the relaxation speed:

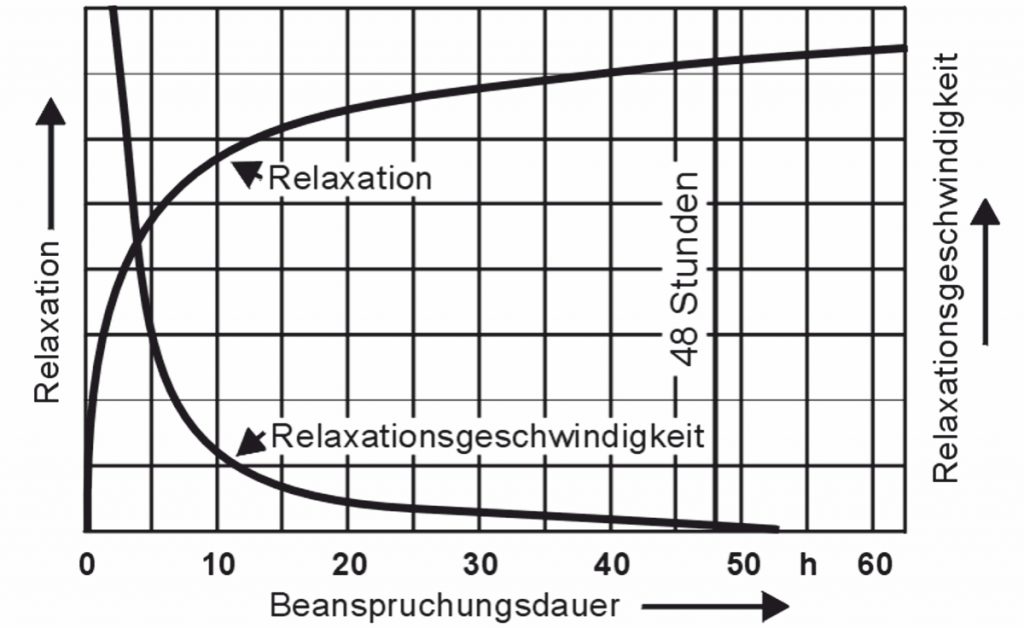
Relaxation graphics - Gutekunst Federn — Time course of the relaxation and the relaxation speed in helical compression springs

The relaxation values after 48 hours are considered to be characteristic values, although the relaxation is not yet completely complete at this point in time. Material-dependent relaxation diagrams can be found in EN 13906-1. These are only to be included by the designer if high demands are placed on the constancy of the spring force. The relaxation at different temperature states is used in the calculation in Spring calculation program WinFSB from Gutekunst Federn, available at www.federnshop.com , shown with.

The right choice of spring material

Metal springs must be manufactured from a suitable spring material and designed and shaped in such a way that they return to their original shape after the applied load has been removed. This property is expressed in the modulus of elasticity and in the sliding module. These Material parameters express the relationship between tension and elongation and should have as high a value as possible.

In addition, spring materials should:

high elasticity limits, i.e. a large, purely elastic range,
the corresponding tensions also at elevated temperatures endure without major loss of strength (low relaxation),
have a high fatigue strength (fine-grain structure, free of impurities),
have sufficient deformability,
have a surface that is as slippery as possible,
withstand certain requirements for corrosion protection,
be electrically conductive or non-magnetic.

Elasticity and sliding moduli of various spring materials

Spring material	Modulus of elasticity [N/mm²]	G module [N/mm²]
Patented drawn spring steel wire according to EN 10270-1	206000	81500
Oil tempered valve spring wire according to EN 10270-2	206000	81500
Hot rolled steel according to EN10089	206000	78500
Cold rolled strip according to EN 10132	206000	78500
X10 CrNi 18 8 (1.4310)	185000	70000
X7 CrNiAl 17 7 (1.4568)	195000	73000
X5 CrNiMo 17-12-2 (1.4401)	180000	68000
CuSn6 R950 according to EN 12166	115000	42000
CuZn36 R700 according to EN 12166	110000	39000
CuBe2 according to EN 12166	120000	47000
CuNi18Zn20 according to EN 12166	135000	45000
CuCo2Be according to EN 12166	130000	48000
Inconel X750	213000	76000
Nimonic 90	213000	83000
Hastelloy C4	210000	76000
Titanium alloy TiAl6V4	104000	39000

Influence of working temperature on spring material selection

Behavior at elevated working temperatures

The level of the working temperature can significantly influence the function of a spring, as the tendency to relaxation increases with increasing temperature. After evaluating the relaxation diagrams, the following limit temperatures can be set for the most important spring materials.

Limit temperatures of spring materials with minimal relaxation

Spring material	Maximum working temperature in ° C at
	high load	low load
Patented drawn spring steel wire according to EN 10270-1	60-80	80-150
Oil tempered valve spring wire according to EN 10270-2	80-160	120-160
X10CrNi 18.8 (1.4310)	160	250
X7CrNiAl 17.7 (1.4568)	200	350
X5CrNiMo 17-12-2 (1.4401)	160	300
CuSn6	80	100
CuZn36	40	60
CuBe2	80	120
CuNi18Zn20	80	120
Inconel X750	475	550
Nimonic90	500	500

In addition, take the important for the spring function Material properties modulus of elasticity and shear modulus decreases with increasing temperature. Both the shear modulus and the modulus of elasticity are determined at higher temperatures using the following formula, with the material parameters at room temperature (20 ° C) serving as the basis.

G_{t}=G_{20}=\frac{3620-T}{3600}

or.

E_{t}=E_{20}=\frac{3620-T}{3600}

This enables the designer to determine the actual spring forces at the expected operating temperature.

Behavior at low operating temperatures

When used in cooling systems, in space or when it is very cold in winter, temperatures as low as – 200 ° have to be endured. Despite rising tensile strenght low temperatures have an unfavorable effect, as the toughness of the materials decreases and brittle fractures can occur. Stainless spring steels as well as copper and nickel alloys are preferable to the patented spring wires and valve spring wires when used at low temperatures. The following table shows the limit temperatures.

Recommendations for use at low temperatures

Spring material	Minimum working temperature in ° C
Patented drawn spring steel wire according to EN 10270-1	-60
Oil tempered valve spring wire according to EN 10270-2	-60
X10CrNi 18.8 (1.4310)	-200
X7CrNiAl 17.7 (1.4568)	-200
X5CrNiMo 17-12-2 (1.4401)	-200
CuSn6	-200
CuZn36	-200
CuBe2	-200
CuNi18Zn20	-200
Inconel X750	-100
Nimonic90	-100

Use of spring systems

For structural reasons, it is also possible to use several springs to absorb forces and movements. Simple Spring systems are Parallel – and Series connections .

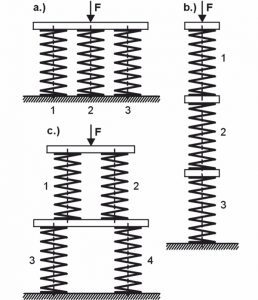
Spring systems graphics - Gutekunst Federn — Spring systems a) parallel connection, b) series connection, c) Mixing circuit

a) Parallel connection

The springs are arranged in such a way that the external load (F) is proportionally divided between the individual springs, but the travel of the individual springs is the same. So it results:

s=s1=s2=s3=...

(total suspension travel)

F=F1+F2+F3+...

(total spring force)

R=R1+R2+R3+...

(total spring rate)

The spring rate of the overall system of a parallel connection is always greater than the spring rate of the individual springs

b) Series connection

The springs are arranged one behind the other, so that the same force acts on each spring, but the spring travel is divided between the individual springs. It results:

s=s1+s2+s3+...

(total suspension travel)

F=F1=F2=F3=...

(total spring force)

R=\frac{1}{\frac{1}{R1}+\frac{1}{R2}+\frac{1}{R3}+...}

(Total spring rate)

The spring rate of the overall system of a series connection is always smaller than the spring rate of the individual springs

c) Mixed circuit

Several springs are connected in parallel and one behind the other. Because of the equilibrium, R1 = R2 and R3 = R4 must be. In the case shown, the following applies: