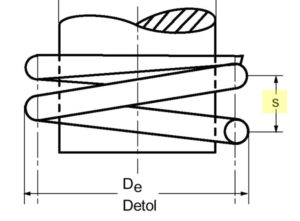
The pitch “S” of compression springs, also known as the coil pitch, refers to the distance between their individual coils (wire center to wire center) and is calculated and determined using the following formulas. It is measured parallel to the longitudinal axis from wire center to wire center. The pitch of a compression spring is particularly important because it has a direct effect on the suspension behavior. A compression spring that has a greater pitch for the same length is, for example, stronger than a spring with a lower pitch.
The gradient of compression springs can be calculated with the following formulas:
- Compression springs with applied and ground spring ends:
\Large S = \frac{(L0-d)}{n}
- Compression springs with unmounted and unpolished spring ends:
\Large S = \frac{(L0-2.5 \cdot d)}{n}
The following applies:
S = slope
L0 = length of the unloaded spring
d = wire diameter
n = number of turns
In order to be able to use the different spring properties with different slopes, both the minimum distance and the maximum slope must be observed for the winding slope.
The minimum distance between effective coils can be calculated as follows:
\Large Sa = (\frac{0.0015 \cdot D^{{2}}}{d} + 0.1 \cdot d) n \cdot 1.5
The maximum gradient can be determined using the following formula:
\Large Smax = 0.7 \cdot Di
The following applies:
Sa = minimum distance
Smax = maximum gradient
D = mean coil diameter
d = wire diameter
n = number of turns
Di = inner coil diameter
In rare exceptional cases, the maximum pitch can also exceed 0.7 times the inner coil diameter. In order to ensure that the spring functions correctly, all spring parameters must be checked for their feasibility.
To calculate the slope, Gutekunst offers you that Spring calculation program WinFSB at free disposal. This allows you to test the effects of the different gradients yourself. To do this, change the number of turns “n” on the properties page.
For the interpretation of a suitable Compression-, Extension- or Torsion spring please contact our technical department directly by phone (+49) 035 877 227-13 or service@gutekunst-co.com.
For more information: