„Die Verformung eines elastischen Körpers ist proportional zur wirkenden Kraft“ – diese fundamentale Erkenntnis des Physikers Robert Hooke revolutionierte vor über 300 Jahren den Maschinenbau. Denn das Hookesche Gesetz ermöglichte die präzise Berechnung von Metallfedern. Warum das Hookesche Gesetz auch heute noch von hoher Relevanz für die moderne Industrie ist, erfahren Sie in diesem Beitrag.

Im Jahr 1676 veröffentlichte der britische Physiker Robert Hooke sein bahnbrechendes Werk „De Potentia Restitutiva“ (Über die wiederherstellende Kraft), in dem er erstmals das formulierte, was später als Hookesches Gesetz bekannt wurde. Die Entdeckung stammte aus seinen Experimenten mit Federn und elastischen Materialien, bei denen er eine fundamentale Beziehung beobachtete: Die Kraft, die benötigt wird, um eine Feder zu dehnen oder zu komprimieren, ist proportional zur Strecke, um die sie aus ihrer Ruhelage gedehnt oder komprimiert wird. Hooke fasste diese Erkenntnis elegant mit dem lateinischen Satz „ut tensio, sic vis“ zusammen — wie die Dehnung, so die Kraft. Die einfache, aber tiefgründige Beobachtung legte den Grundstein für das Verständnis der elastischen Verformung von Materialien und wurde zu einem der Grundprinzipien der Maschinenbautechnik, insbesondere bei der Konstruktion und Anwendung von Metallfedern. Diese allgegenwärtigen mechanischen Komponenten wandeln mechanische Energie in potentielle Energie um, wenn sie komprimiert oder gedehnt werden, und speichern und geben diese Energie bei Bedarf wieder ab — eine direkte Anwendung des Hookeschen Gesetzes in der Praxis.
Table of Contents
Folgende Faktoren beeinflussen das elastische Verhalten
Hohe Elastizitätsgrenze bei gleichzeitig hoher Verformbarkeit (Duktilität)
Das Elastizitätsmodul ist ein Materialkennwert aus der Werkstofftechnik und definiert die Steigung des Graphen, auch Hookesche Gerade genannt, im Spannungs-Dehnungs-Diagramm. Dieser Kennwert beschreibt den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers in einem linear-elastischem Verhalten. Das Elastizitätsmodul ist unter den Abkürzungen E-Modul oder als Formelzeichen E in der Federnberechnung bekannt; es hat die Einheit „N/mm²“ einer mechanischen Spannung.
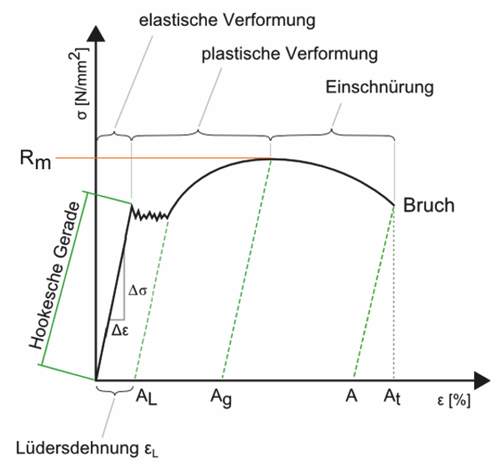
Ausreichende Zugfestigkeit „Rm“
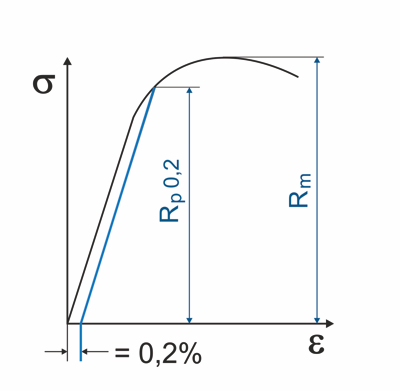
Federstahl besitzt im Vergleich zu anderen Stählen eine deutlich höhere Zugfestigkeit „Rm“ und kann somit bis zu einer bestimmten Spannung – Elastizitätsgrenze „Rp“ – verformt werden. Nach Entlastung kehrt der Federstahl wieder in die Ausgangsstellung zurück, ohne dabei dauerhaft verformt zu werden. Da diese Elastitzitätsgrenze „Rp“ (Hookesche Gerade) fließend ist, wird bei Federstählen in der Regel die Dehngrenze „Rp0,2“ angewendet. Dabei wird eine Parallele zur Hookesche Gerade im Abstand von 0,2 % als Ersatz zur Elastizitätsgrenze gezogen. Federstahl hat zum Beispiel eine Zugfestigkeit „Rm“ von 1200 bis 2940 N/mm², verglichen mit 360 N/mm² beim Baustahl S235JR. Hierbei ist der maßgebliche Unterschied das Streckgrenzenverhältnis „Rp/Rm“, d.h. das Verhältnis von Elastizitätsgrenze zu Zugfestigkeit des Werkstoffs, welches bei Federstählen normalerweise bei >85 % liegt. Die Elastizität als Hauptmerkmal eines Federstahls wird beim Herstellungsprozess durch eine spezielle Legierung unter Zugabe von Silizium (Si), Mangan (Mn), Chrom (Cr), Vanadium (V), Molybdän (Mo) und Nickel (Ni) erreicht.
Zusammensetzung des Materials
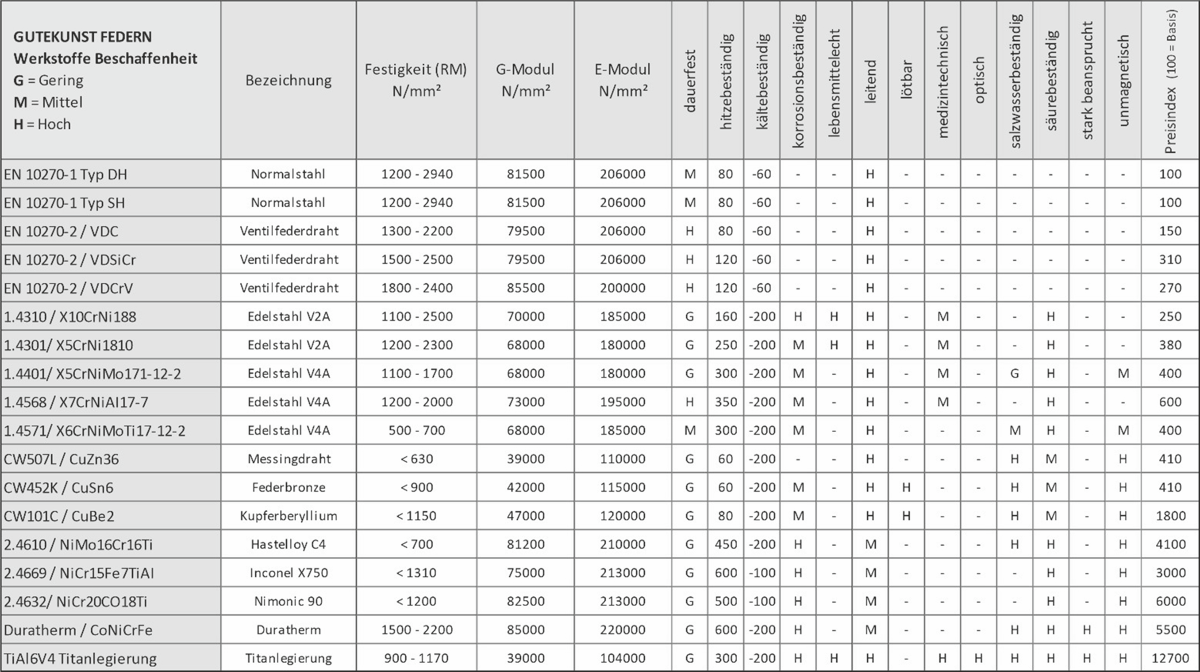
Welche Materialeigenschaften sind zur Einhaltung des Hookeschen Gesetzes entscheidend bei der Auswahl des richtigen Federstahls? Neben den grundsätzlichen Werkstoffeigenschaften wie rostfrei, elektrisch leitend, hochtemperaturfähig etc. sind es Material-Kennwerte wie das G-Modul (Schubmodul), E-Modul (Elastizitätsmodul) und die Zugfestigkeit [Rm], die Einfluss auf die Federkonstante und das Federverhalten nehmen. Nachfolgend aufgelistet die Eigenschaften der wichtigsten Federstähle (ohne Gewähr):
Geometrie und Bauform der Metallfeder
Die geometrische Konfiguration einer Metallfeder wird durch folgende Faktoren beeinflusst:
Geometrische Faktoren für Druckfedern, Zugfedern und Schenkelfedern
- Drahtdurchmesser (d): Zunehmende Drahtstärke erhöht die Federsteifigkeit (Kraft) exponentiell
- Mittlerer Windungsdurchmesser (D): Größerer Windungsdurchmesser verringert die Federsteifigkeit (Kraft)
- Anzahl der aktiven Windungen (n): Weniger Windungen vergrößern die Federsteifigkeit (Kraft) der Feder
Dazu bestimmt die Federbauform, ob die Metallfeder ein perfekt lineares Verhalten aufweist oder unter bestimmten Bedingungen vom Hookeschen Gesetz abweicht. Beispielsweise zeigen Federn mit variabler Steigung zwischen den Windungen und konisch zulaufende Metallfedern nichtlineare Kraft-Weg-Beziehungen, was in bestimmten Anwendungen von Vorteil sein kann.
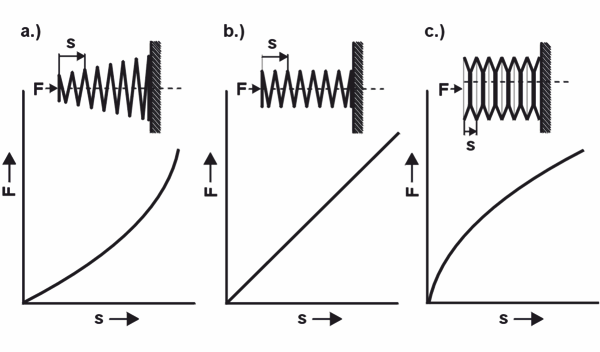
Die Federkennlinie zeigt, wie die Metallfeder sich bei der Arbeit verhält. Sie beschreibt das Verhältnis zwischen Federkraft (F) und Federweg (s). Je nach Bauform der Feder oder eingesetztem Federsystem unterscheidet man in eine lineare (b), progressive (a), degressive (c) Federkennlinie.
Die mathematische Grundlage des Hookeschen Gesetzes
Das Hookesches Gesetz beschreibt die elastische Verformung von Festkörpern in einem linearen Sonderfall des Elastizitätsgesetzes. Dabei verändert sich die elastische Kraft des Körpers mit dem Ausdehnen oder dem Zusammendrücken. Bei der Anwendung von Druckfedern, Zugfedern und Schenkelfedern mit zylindrischer Bauform besteht ein linearer Zusammenhang zwischen Ausdehnung und Kraft.
Durch eine andere Gestaltung – wie durch einen konischen Windungsdurchmesser oder einen unterschiedlichen Windungsabstand – lassen sich Metallfedern auch mit einer nicht linearen Verformung herstellen. Grundsätzlich beschreibt das Hookesche Gesetzt die Aufgabe einer Metallfeder: Je länger die Strecke „s“ ist, um die eine Metallfeder gedehnt oder zusammengedrückt wird, desto stärker ist die entgegenwirkende Federkraft „F“ der Feder.
Das Hookesche Gesetz besagt, dass der Federweg „s“ linear von der einwirkenden Kraft „F“ abhängt.
Diese Federkonstante „R“ der elastischen Verformung wird mit der folgenden Formel berechnet:
Formel Hookesches Gesetz: \Large R\ =\ \frac{F}{s}
Dabei gilt:
- R die Federkonstante (Federrate) beschreibt die Steifigkeit der Metallfeder (N/mm)
- F die rückstellende Kraft der Metallfeder – Federkraft (N)
- s die Wegstrecke aus der Ruhelage der Metallfeder – Federweg (mm)
Die Federkonstante „R“ ist abhängig vom Werkstoff und der Bauform der Feder. Mit zunehmender Drahtstärke oder einem kleineren Windungsdurchmesser wird die Federkonstante einer Metallfeder größer. Sie wird in der Einheit Newton pro Millimeter (N/mm) angegeben und ist der Quotient aus der Federkraft „F“ und dem Federweg „s“. Im Hookeschen Gesetz dient die Federkonstante „R“ als Proportionalitätsfaktor und beschreibt die Steifigkeit der Metallfeder. Bei einer Zugfeder zeigt sich das lineare Verhalten bei Belastung mit einem Gewicht. Nach Verdoppelung des Gewichts tritt auch der doppelte Weg „s“ auf.
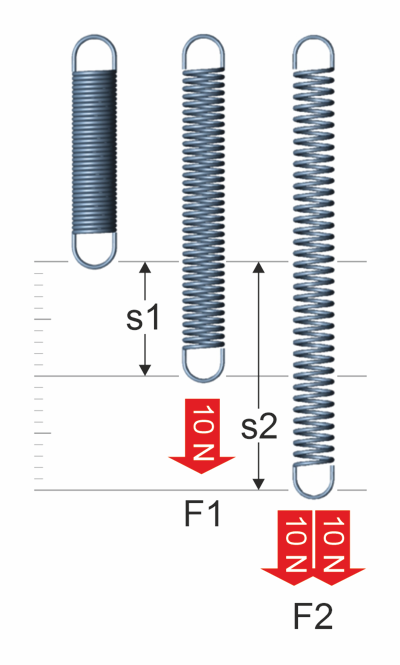
Dieses lineare Verhalten ist maßgeblich wichtig für die Anwendung von Metallfedern als Kraftspeicher, Rückstellkraft, Lastverteilung und bei kraftschlüssigen Verbindungen.
Formel zur Berechnung der Federkonstante für Druckfedern, Zugfedern und Schenkelfedern:
Formel Federkonstante Druckfedern (N/mm)
\Large R=\frac{Gd^{4}}{8D^{3}n}
Formel Federkonstante Zugfedern (N/mm)
\Large R=\frac{Gd^{4}}{8D^{3}n}=\frac{F-F0}{s}
Formel Federmomentrate Schenkelfedern (Nmm)
\Large R_{M}=\frac{M}{\alpha}=\frac{d^{4}E}{3667Dn}
Formelerklärung:
α = Drehwinkel (°)
d = Drahtdurchmesser (mm)
D = mittlerer Windungsdurchmesser (mm)
E = Elastizitätsmodul (N/mm²)
F = Federkraft (N)
G = Gleit- und Schubmodul (N/mm²)
F0 = innere Vorspannkraft
M = Drehmoment (Nmm)
n = Anzahl der federnden Windungen (Stück)
R = Federkonstante (N/mm)
RM = Federmomentrate (Nmm)
s = Federweg (mm)
Die Federkraft wird mit der folgenden Formel berechnet:
\large F = -R \cdot s
Wieso ist die Federkonstante negativ? Das Minuszeichen in der Gleichung bedeutet, dass – bezogen auf die Ruhelage – die Auslenkungsrichtung einer Feder der Federkraft entgegengesetzt ist.
Bestimmung der Elastizitätsgrenze „Rp“
Obwohl die Elastizitätsgrenze „Rp“ die technische Spannungsgrenze des Federstahls beschreibt, wird bei der Berechnung der zulässigen Spannung „Ʈzul“ auf den Zugfestigkeitswert „Rm“ zurückgegriffen. Grund dafür ist, dass die Rp-Werte für viele Federwerkstoffe fehlen bzw. von den Herstellern nicht garantiert werden.
Dabei beträgt die zulässige Schubspannung „Ʈzul“ je nach Federntyp:
Druckfedern » Ʈzul = 0,5 · Rm » bzw. bei Belastung auf Block Ʈczul=0,56 · Rm
Zugfedern » Ʈzul = 0,45 · Rm
Schenkelfedern » σzul = 0,7 · Rm
Elastische Eigenschaften der Federstähle im vorgesehenen Temperaturbereich
Die Höhe der Arbeitstemperatur kann die Funktion einer Metallfeder erheblich beeinflussen, da die Neigung zu Relaxation mit steigender Temperatur zunimmt. Die Relaxation beschreibt den Kraftverlust der Metallfeder bei permanenter Spannung und höheren Temperaturen. Dieser Kraftverlust nimmt mit steigender Temperatur und Belastungsdauer zu.
Er wird prozentual auf die Ausgangskraft „F1“ angegeben.
\large Relaxation\ =\ \frac{∆F·100}{F1}
Auf nachfolgender Grafik wird der prinzipielle Verlauf der Relaxation und der Relaxationsgeschwindigkeit dargestellt.

Hohe Temperaturänderungen können zudem Phasenumwandlungen oder Gefügeveränderungen verursachen. Federmaterialien für Hochtemperaturanwendungen benötigen spezielle Legierungszusätze zur Stabilisierung der Mikrostruktur.
Einschränkungen und praktische Überlegungen
Neben den beschriebenen Faktoren einer optimalen Federauslegung gibt es auch besondere Einflussfaktoren, die einer optimalen Nutzung einer Metallfeder entgegenstehen und zu mehreren Einschränkungen führen.
- Elastizitätsgrenze: Jenseits eines bestimmten Punktes (Streckgrenze) verformen sich Federn dauerhaft.
- Ermüdung: Wiederholte Belastungszyklen können auch innerhalb der Elastizitätsgrenze zum Versagen führen.
- Spannungsrelaxation: Einige Federn verlieren mit der Zeit an Spannung, besonders bei erhöhten Temperaturen.
- Fertigungsvariationen: Toleranzen und Unvollkommenheiten beeinflussen theoretische Berechnungen.
- Umweltfaktoren: Temperatur, Korrosion und chemische Exposition verändern die Federeigenschaften.
Diese Faktoren müssen bei der Auswahl und Konstruktion von Metallfedern für die spezifische Anwendung berücksichtigt werden.
Schlussfolgerung: Die anhaltende Bedeutung von Federn in der Technik
Metallfedern, die von den Prinzipien des Hookeschen Gesetzes bestimmt werden, gehören heute noch zu den vielseitigsten, am häufigsten verwendeten mechanischen Komponenten in der modernen Industrie. Ob in kleinen technischen Anwendungen oder in großen, massiven Industriemaschinen: Ihre Fähigkeit, Energie auf vorhersehbare, kontrollierbare Art zu speichern und freizusetzen macht Metallfedern in unzähligen Anwendungen unersetzlich.
Neue Legierungen erweitern das Leistungsspektrum von Metallfedern und ermöglichen Anwendungen in extremeren Umgebungen sowie mit größerer Effizienz. Heute erlaubt die computergestützte Modellierung den Ingenieuren zunehmend komplexe Federgeometrien zu entwerfen, die präzise maßgeschneiderte Kraft-Weg-Beziehungen liefern und über das durch das klassische Hookesche Gesetz beschriebene lineare Verhalten hinausgehen.
Die Grundlagen der Federmechanik befähigen Ingenieure, die einfachen, aber leistungsstarken Komponenten auf innovative Weise zu nutzen. Trotz ihres altertümlichen Ursprungs – Bronzefedern sind bis ins 15. Jahrhundert v. Chr. nachweisbar – entwickeln sich Federn permanent weiter. Metallfedern bleiben das Herzstück mechanischer Systeme in praktisch jeder Branche. Robert Hookes Beobachtungen vor über drei Jahrhunderten waren bahnbrechend und sind auch weiterhin von Nutzen für die Industrie.
Mehr Informationen und weiteres Wissen zu Druck-, Zug- und Schenkelfedern sowie deren Anwendungsgebiete finden Sie auf blog.federnshop.com. Die Technikabteilung von Gutekunst Federn erreichen Sie unter Telefon (+49) 035877 2270 oder technik@gutekunst-co.com.
Weitere Informationen: