Auslegung Metallfedern — Teil 2 „Berechnung“ › Gutekunst Federn › Berechnungsformeln, Druckfedern, Federberechnung, Formeln, Schenkelfedern, Zugfedern

Im ersten Teil dieser zweiteiligen Serie hat Gutekunst Federn über die Grundlagen der Federauslegung informiert. Im vorliegenden zweiten Teil finden Sie die konkreten Berechnungsdaten zur Auslegung von Druckfedern, Zugfedern und Schenkelfedern (Drehfedern). Zur individuellen Berechnung steht Ihnen auch das Gutekunst Federnberechnungsprogramm WinFSB zur Verfügung.

Ziel des Federentwurfes einer Druckfeder, Zugfeder oder Schenkelfeder ist es, die für die gegebene Aufgabe unter Berücksichtigung aller Umstände wirtschaftlichste Feder zu finden, die auch in den zur Verfügung stehenden Raum passt und die geforderte Lebensdauer erreicht. Neben diesen fertigungstechnischen und werkstofflichen Anforderungen kommt der richtigen Federauslegung besondere Bedeutung zu.

Vor der Federnberechnung sollten folgende Anforderungen der Metallfeder zusammengestellt werden:

1. Belastungsart (statisch oder dynamisch)

2. Lebensdauer

3. Einsatztemperatur

4. Umgebungsmedium

5. Notwendige Kräfte und Federwege

6. Vorhandener Einbauraum

7. Toleranzen (Druckfedern, Zugfedern)

8. Einbausituation (Knickung, Querfederung)

Jede Federberechnung besteht aus zwei Stufen:

Funktionsnachweis: Überprüfung der Federrate, der Kräfte und der Federwege, des Schwingungsverhaltens etc.
Festigkeitsnachweis: Überprüfung auf Einhaltung der zulässigen Spannungen bzw. Dauerfestigkeitsnachweis.

Dazu ist eine iterative Vorgehensweise erforderlich.

Der Festigkeitsnachweis basiert auf der Entscheidung, ob die Feder statisch, quasistatisch oder dynamisch beansprucht wird. Folgende Kriterien sollten zur Abgrenzung herangezogen werden:

Statische oder quasistatische Beanspruchung: zeitlich konstante (ruhende) Belastung oder zeitlich veränderliche Belastung mit weniger als 10000 Hüben insgesamt.
Dynamische Beanspruchung: zeitlich veränderliche Belastungen mit mehr als 10000 Hüben. Die Feder ist meist vorgespannt und periodischer Schwellbelastung mit sinusförmigen Verlauf ausgesetzt, die zufällig (stochastisch) erfolgt, z.B. bei KFZ-Federungen. In einigen Fällen kommt es zu schlagartigen Kraftänderungen.

Bei der Federdimensionierung sind Beanspruchungsgrenzen festzulegen, die auf den Festigkeitswerten der Werkstoffe basieren und die Beanspruchungsart berücksichtigen. Dazu wird ein Sicherheitsfaktor einbezogen und so die zulässige Spannung ermittelt. Nach einem Vergleich mit der tatsächlich vorhandenen Spannung muss durch iterative Vorgehensweise die Federdimensionierung überarbeitet werden. Dabei gilt: Nennspannung ≤ zulässige Spannung

Table of Contents

Berechnung Druckfedern

Allgemeines

Kaltgeformte zylindrische Druckfedern mit konstanter Steigung kommen in der Praxis am häufigsten zum Einsatz. Der Draht wird durch Winden um einen Dorn kalt umgeformt. Je nach Vorschub des Steigungsstiftes werden der Windungsabstand und die Anlage der Feder reguliert. Nach dem Winden erfolgt das Anlassen, um Eigenspannungen in der Feder abzubauen sowie die Schubelastizitätsgrenze zu erhöhen. Es verringert sich also der Setzbetrag. Die Anlasstemperaturen und -zeiten richten sich nach dem Werkstoff; die Abkühlung erfolgt an Luft bei normaler Raumtemperatur.

Weitere wichtige Arbeitsgänge in der Federherstellung sind das Schleifen und Setzen. Die Federenden werden in der Regel ab einer Drahtstärke von 0,5 mm geschliffen, um eine planparallele Lagerung der Feder sowie eine optimale Krafteinleitung zu gewährleisten.

Übersteigt bei Belastung der Feder die Schubspannung den zulässigen Wert, tritt eine bleibende Verformung ein, die sich in der Verringerung der ungespannten Länge äußert. Dieser Vorgang wird in der Federntechnik als „Setzen“ bezeichnet, was mit den Begriffen „Kriechen“ und „Relaxation“ aus der Werkstofftechnik gleichzusetzen ist. Um dem entgegenzuwirken, werden die Druckfedern um den zu erwartenden Setzbetrag länger gewunden und später auf Blocklänge zusammengedrückt. Dieses Vorsetzen ermöglicht eine bessere Werkstoffauslastung und erlaubt im späteren Einsatz eine höhere Belastung.

Berechnungsformeln zylindrische Druckfeder

Die Berechnung der Druckfeder basiert auf den Berechnungsgleichungen aus der DIN EN 13906-1:

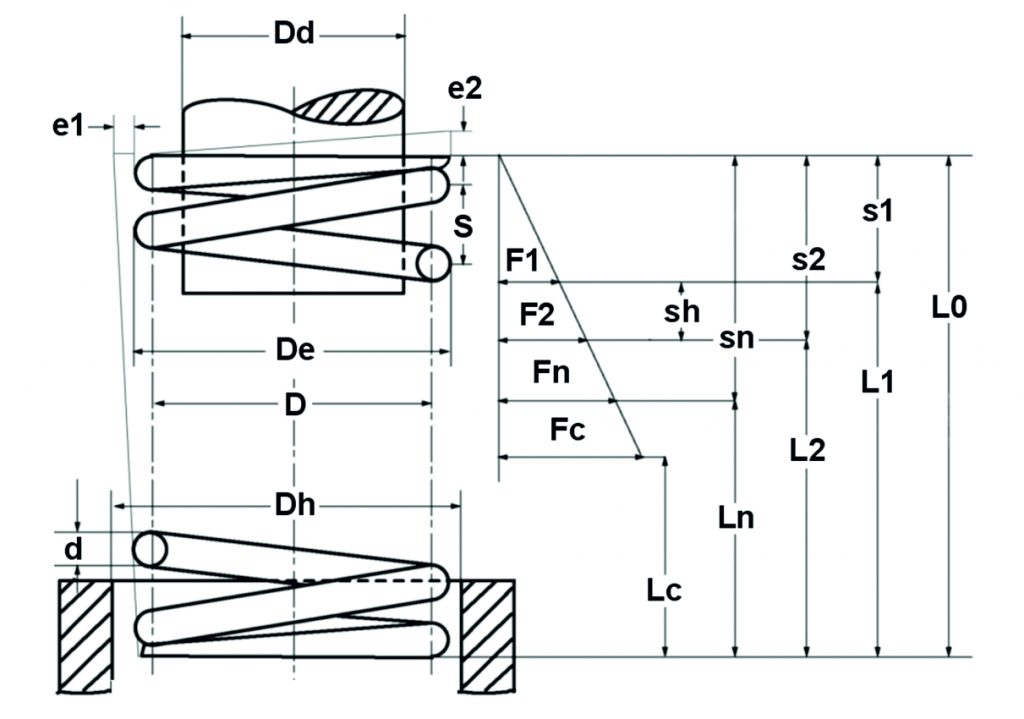
Bild: Theoretisches Druckfederdiagramm

Funktionsnachweis Druckfedern

Für zylindrische Druckfedern aus Draht mit Kreisquerschnitt gilt:

Formel Federrate: $\Large R=\frac{ Gd^{4}}{8D^{3}n}$

aus R=F/s folgt:

Federkraft: $\Large F=\frac{ Gd^{4}s}{8D^{3}n}$

sowie:

Federweg: $\Large s=\frac{8D^{3}nF}{Gd^{4}}$

Festigkeitsnachweis Druckfeder

Nach Festlegung der Federdimensionen muss der Festigkeitsnachweis geführt werden. Dazu wird die vorhandene Schubspannung ermittelt:

Spannung aus Kraft: $\Large \tau=\frac{8DF}{\pi d^{3}}$

Spannung aus Weg: $\Large \tau=\frac{Gds}{\pi n D^{2}}$

Während die Schubspannung τ für die Auslegung statisch oder quasistatisch beanspruchter Federn heranzuziehen ist, gilt die korrigierte Schubspannung τ_kfür dynamisch beanspruchte Federn. Die Schubspannungsverteilung im Drahtquerschnitt einer Feder ist ungleichmäßig, die höchste Spannung tritt am Federinnendurchmesser auf. Mit dem Spannungskorrekturfaktor k, der vom Wickelverhältnis (Verhältnis von mittlerem Durchmesser zur Drahtstärke) der Feder abhängt kann die höchste Spannung annähernd ermittelt werden. Für dynamisch beanspruchte Druckfedern ergibt sich also:

Korrigierte Schubspannung: $\Large \tau_{k}=k\tau$

wobei für k gilt (nach Bergsträsser):

\Large k=\frac{\frac{D}{d}+0,5}{\frac{D}{d}-0,75}

Nun erfolgt der Vergleich mit der zulässigen Spannung. Diese ist wie folgt definiert:

Zulässige Spannung:

\Large \tau_{{zul}}=0,5\cdot R_{{m}}

und

\Large \tau_{{czul}}=0,56\cdot R_{{m}}

Die Werte für die Mindestzugfestigkeit R_m sind von der Drahtstärke abhängig und in den Normen der entsprechenden Werkstoffe zu finden.

In der Regel müssen sich Druckfedern bis zur Blocklänge zusammendrücken lassen, deshalb ist die zulässige Spannung bei Blocklänge t_czul zu berücksichtigen.

Bei dynamischer Beanspruchung müssen Unter- und Oberspannung (t_k1 und t_k2) des entsprechenden Hubes ermittelt werden. Die Differenz ist die Hubspannung. Sowohl die Oberspannung als auch die Hubspannung dürfen die entsprechenden zulässigen Werte nicht überschreiten. Diese sind den Dauerfestigkeitsschaubildern der EN 13906-1:2002 zu entnehmen. Halten die Spannungen diesem Vergleich stand, ist die Feder dauerfest bei einer Grenzlastspielzahl von 10⁷.

Geometriebeziehungen bei Druckfedern

Federkenngröße	Berechnungsgleichung
Gesamtzahl der Windungen	nt = n + 2
Blocklänge der geschliffenen Feder	Lc = nt dmax
Blocklänge der ungeschliffenen Feder	Lc = (nt + 1,5)dmax
Kleinste nutzbare Länge	Ln = Lc + Sa
Ungespannte Länge	L0 = Ln + sn
Summe der Mindestabstände zwischen den Windungen	$\Large S_{a}=\left (0,0015 \frac{D^{2}}{d} + 0,1d \right )\cdot n$
Vergrößerung des Außendurchmessers bei Belastung Steigung	$\Large \triangle D_{e}=0,1\frac{S^{2}-08Sd-0,2d^{2}}{D}$ $\Large S=\frac{L0-d}{n}$ (geschliffen) $\Large S=\frac{L0-2,5d}{n}$ (ungeschliffen)
Knickfederweg (gültig für verschiedene Lagerungsbeiwerte n, siehe EN 13906-1:2002)

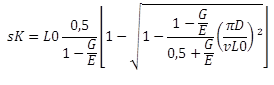Alle dynamisch beanspruchten Federn mit einer Drahtstärke > 1 mm sollten kugelgestrahlt werden. Dadurch ist eine Steigerung der Dauerhubfestigkeit zu erreichen. Nachdem sowohl der Funktionsnachweis als auch der Festigkeitsnachweis geführt wurde, sind noch verschiedene Geometrieberechnungen auszuführen und zu berücksichtigen, um die Feder passend in die Konstruktion des Bauteils einfügen zu können. Die Blocklänge kann nicht unterschritten werden, weil die Windungen fest aneinander liegen, die kleinste nutzbare Länge sollte nicht unterschritten werden, weil dann ein linearer Kraftverlauf sowie dynamische Belastbarkeit nicht mehr gewährleistet sind. Außerdem sind die zulässigen Toleranzen nach DIN 2095 zu berücksichtigen.

Berechnung Zugfedern

Allgemeines

Zugfedern werden genau wie Druckfedern um einen Dorn gewunden, jedoch ohne Windungsabstand und mit verschiedenen Ösenformen/ Federenden zur Befestigung der Feder. Die Windungen werden dabei fertigungstechnisch eng aneinandergepresst. Diese innere Vorspannung F₀ ist vom Wickelverhältnis abhängig und nicht beliebig hoch fertigbar. Anhaltswerte für die Höhe der Vorspannung liefert die Berechnungssoftware WinFSB von Gutekunst Federn nach Eingabe der jeweiligen Federdaten.

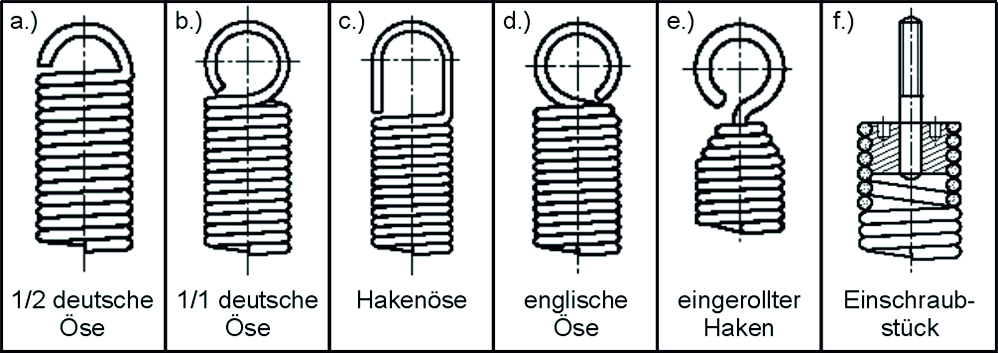
Bild: Häufige Ösenformen: a.) halbe deutsche Öse; b.) ganze deutsche Öse; c.) Hakenöse; d.) englische Öse; e.) eingerollter Haken; f.) Einschraubstück

Der Vorteil von Zugfedern besteht in der Knickfreiheit, Nachteil sind der größere Einbauraum sowie die vollständige Unterbrechung des Kraftflusses beim Federbruch.

Berechnungsformeln zylindrische Zugfeder

Entsprechend den Berechnungsgleichungen für Druckfedern, jedoch unter Berücksichtigung der Vorspannkraft gelten folgende Zusammenhänge für zylindrische Zugfedern aus Runddraht (siehe auch Bild 1.8):

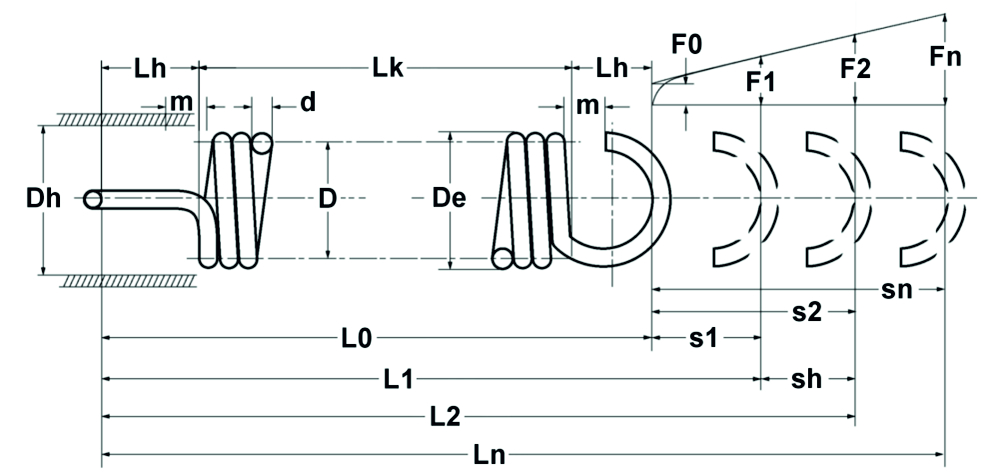
Bild: Theoretisches Zugfederdiagramm

Funktionsnachweis Zugfeder

Für zylindrische Zugfedern aus Draht mit Kreisquerschnitt gilt:

Federrate: $\Large R=\frac{Gd^4}{8D^3n}=\frac{F-F0}{s}$

aus R=F/s folgt:

Federkraft: $\Large F=\frac{Gd^4s}{8D^3n}+F0$

sowie:

Federweg: $\Large s=\frac{8D^3n(F-F0)}{Gd^4}$

Festigkeitsnachweis Zugfedern

Wie auch bei Druckfederberechnungen ist die vorhandene Schubspannung zu ermitteln.

Schubspannung: $\Large \tau=\frac{8DF}{\pi d^3}$

Ebenso muss für dynamische Beanspruchung die korrigierte Hubspannung berechnet werden.

Korrigierte Schubspannung: $\Large \tau_{{k}}=k\tau$

Zulässige Spannung: $\Large \tau_{{zul}}=0,45 \cdot R_{{m}}$

Die vorhandene maximale Spannung t_n beim größten Federweg s_n wird der zulässigen Spannung gleichgesetzt. Um jedoch Relaxation zu vermeiden, sollten in der Praxis nur 80 % dieses Federweges ausgenutzt werden.

\Large s_{{2}}=0,8 \cdot s_{{n}}

Für dynamische Beanspruchungen können keine allgemeingültigen Dauerfestigkeitswerte angegeben werden, da unter Umständen an den Biegestellen der Ösen zusätzliche Spannungen auftreten, die zum Teil über die zulässigen Spannungen hinausgehen können. Zugfedern sollten daher möglichst nur statisch beansprucht werden. Wenn sich dynamische Beanspruchung nicht vermeiden lässt, sollte man auf angebogene Ösen verzichten und eingerollte bzw. eingeschraubte Endstücke einsetzen. Sinnvoll ist ein Lebensdauertest unter späteren Einsatzbedingungen. Eine Oberflächenverfestigung durch Kugelstrahlen ist wegen der eng aneinander liegenden Windungen nicht durchführbar.

Geometriebeziehungen bei Zugfedern

Federkenngröße	Berechnungsgleichung
Körperlänge	LK = (nt + 1)d
Ungespannte Länge	L0 = LK + 2 LH
Ösenhöhe halbe deutsche Öse	LH = 0,55Di bis 0,80Di
Ösenhöhe ganze deutsche Öse	LH = 0,80Di bis 1,10Di
Ösenhöhe Hakenöse	LH > 1,10Di
Ösenhöhe englische Öse	LH = 1,10Di

Die zulässigen Fertigungstoleranzen nach DIN 2097 sind zu berücksichtigen.

Berechnung Schenkelfedern (Drehfedern)

Allgemeines

Gewundene zylindrische Schenkelfedern (Drehfedern) haben im Wesentlichen die gleiche Form wie zylindrische Druck– und Zugfedern, jedoch mit Ausnahme der Federenden. Diese sind schenkelförmig abgebogen, um eine Verdrehung des Federkörpers um die Federachse zu ermöglichen. Damit sind sehr viele verschiedene Einsatzgebiete zu verzeichnen, z.B. als Rückstell- oder Scharnierfedern. Die Aufnahme der Drehfeder sollte auf einem Führungsdorn und die Belastung nur im Wickelsinn erfolgen. Der Innendurchmesser verkleinert sich hierbei. Die Federn werden üblicherweise ohne Steigung gewunden. Ist jedoch Reibung absolut unerwünscht, können Drehfedern auch mit Windungsabstand gefertigt werden. Bei dynamischer Beanspruchung ist darauf zu achten, dass an den Federenden keine scharfkantigen Abbiegungen bestehen, um unberechenbare Spannungsspitzen zu vermeiden.

Berechnungsformeln zylindrische Schenkelfedern (Drehfedern)

Die Berechnung erfolgt nach den Richtlinien der EN 13906-3:2001:

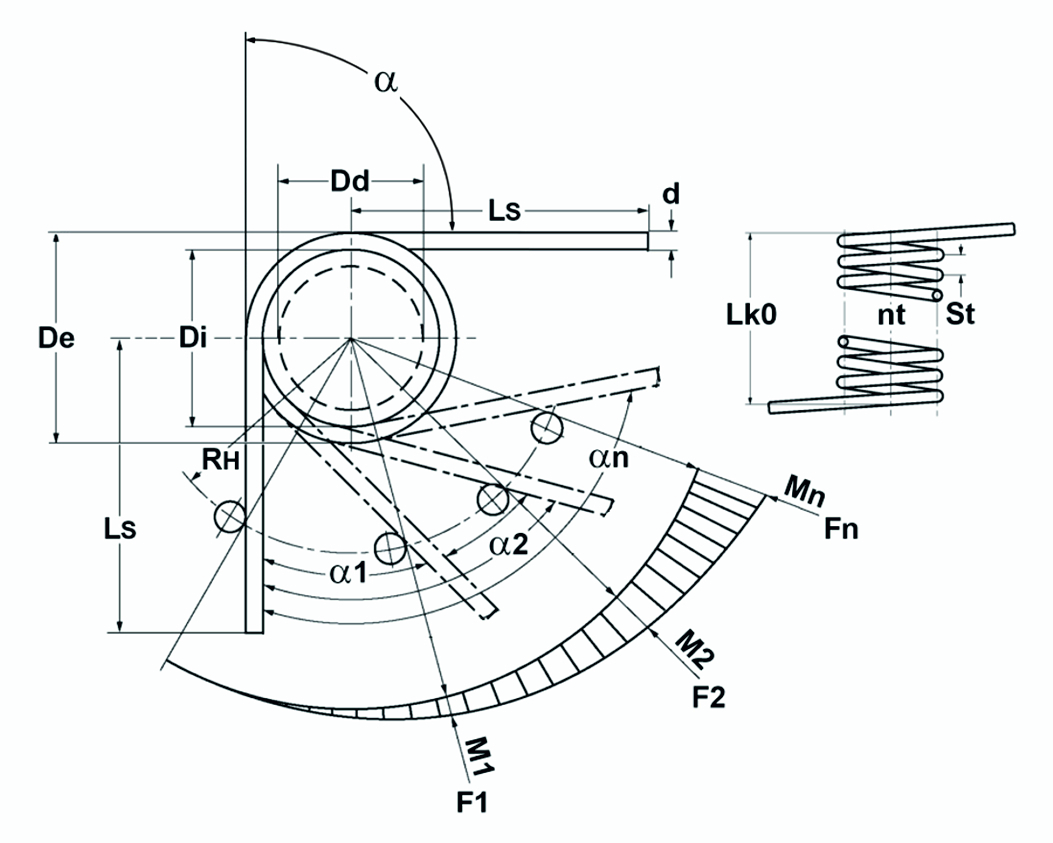
Bild: Theoretisches Schenkelfeder- / Drehfederdiagramm

Funktionsnachweis Schenkelfedern (Drehfedern)

Federmomentrate: $\Large R_{M}=\frac{M}{\alpha}=\frac{d^4E}{3667Dn}$

Federmoment: $\Large M=FR_{H}=\frac{d^4E\alpha}{3667Dn}$

Drehwinkel: $\Large \alpha=\frac{3667DMn}{Ed^4}$

Festigkeitsnachweis Schenkelfedern (Drehfedern)

Die vorhandene Biegespannung wird ermittelt und mit der zulässigen Spannung verglichen. Bei dynamischer Beanspruchung muss wiederum die korrigierte Spannung zum Vergleich herangezogen werden.

Biegespannung: $\Large \sigma=\frac{32M}{\pi d^3}$

Korrigierte Biegespannung: $\Large \sigma_{{q}}=q \sigma$

wobei für q gilt:

\Large q=\frac{\frac{D}{d}+0,07}{\frac{D}{d}-0,75}

Zulässige Biegespannung: $\Large \sigma_{{zul}}=0,7Rm$

Bei dynamischer Beanspruchung müssen Unter- und Oberspannung (t_k1 und t_k2) des entsprechenden Hubes ermittelt werden. Die Differenz ist die Hubspannung. Sowohl die Oberspannung als auch die Hubspannung dürfen die entsprechenden zulässigen Werte nicht überschreiten. Diese sind für Federstahldraht den Dauerfestigkeitsschaubildern der EN 13906-3:2001 zu entnehmen. Halten die Spannungen diesem Vergleich stand, ist die Feder dauerfest bei einer Grenzlastspielzahl von 10⁷.

Geometriebeziehungen bei Schenkelfedern (Drehfedern)

Federkenngröße	Berechnungsgleichung
Verkleinerung des Innendurchmessers bei maximaler Belastung	$\Large Di_{n}=\frac{Dn}{n+\frac{\alpha}{360}}-d$
Unbelastete Körperlänge	$\Large Lk=(n+1,5)d$
Körperlänge im maximal belasteten Zustand	$\Large Lk_{n}=(n+1,5+\frac{\alpha}{360})d$
Federweg	$\Large s_{n}= \frac{\alpha_{n}R_{H}}{57,3}$

Zusätzlich müssen die Fertigungstoleranzen nach DIN 2194 berücksichtigt werden.

Eine Zusammenfassung des Beitrags „Auslegung einer Metallfeder“, bestehend aus Teil 1 „Grundlagen“ und Teil 2 „Berechnung“, finden Sie auch zum Herunterladen im Gutekunst Federn 1×1.

Sollten Sie Bedarf an einer individuellen Federauslegung haben, so mailen Sie uns einfach die Eckdaten der benötigten Metallfeder an technik@gutekunst-co.com , kontaktieren unsere Technik per Telefon unter (+49) 035877 227-11 oder verwenden Sie unter https://www.federnshop.com das Gutekunst Federnberechnungsprogramm WinFSB zur freien Berechnung von Druckfedern, Zugfedern und Schenkelfedern.

Weitere Informationen: