Charakteristická křivka pružiny ukazuje, jak se kovová pružina chová během provozu. Popisuje vztah mezi silou pružiny(F) a dráhou pružiny(s). V závislosti na konstrukci pružiny nebo použitém systému pružin se rozlišuje mezi lineární (b), progresivní(a), degresivní(c) nebo kombinovanou charakteristikou pružiny.
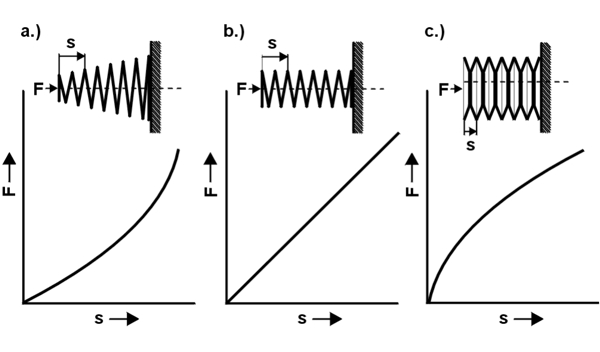
U kuželové konstrukce pružiny a u smíšeného obvodu jednotlivých pružinse získá progresivní charakteristická křivka(a), která s rostoucí výchylkou zvyšuje sílu. Lineární charakteristika pružiny(b), která s rostoucí výchylkou rovnoměrně uvolňuje sílu, se získá při válcovém provedení a při sériovém nebo paralelním zapojení. Křivka degresivní charakteristiky pružiny(c), která s rostoucí výchylkou snižuje sílu, je dosažena pomocí sloupku talířové pružiny.
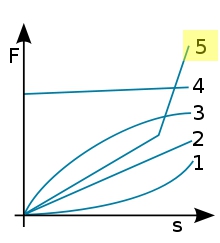
Kombinovanou charakteristiku pružiny(5), která v určitých stavech průhybu prudce mění silové charakteristiky, lze dosáhnout kombinovanými konstrukcemi pružin a speciálními sériovými nebo smíšenými obvody jednotlivých pružin. Křivka charakteristiky pružiny(4) s vysokou předpínací silou a nízkou silovou křivkou je dosažena pomocí měkké předpínací pružiny.
Rychlost pružení(R) je sklon charakteristické křivky pružiny v diagramu pružiny. Při lineární charakteristice pružiny je tuhost pružiny konstantní. Pružiny se zakřivenou charakteristikou pružiny mají proměnnou rychlost pružení. Pro lineární charakteristiky pružin platí následující:
Pro tlačné a tažné pružiny
\Large R = \frac{F2 - F1}{s2 -s1}
Pro torzní pružiny / torzní pružiny
\Large R = \frac{M2 - M1}{\alpha2 -\alpha1}
Dodatečné informace:
- Výpočet celkové pružnosti pro paralelní, sériové a smíšené obvody