The modulus of elasticity is a material parameter from materials engineering and defines the slope of the graph in the stress-strain diagram. This characteristic describes the relationship between tension and strain in the deformation of a solid body in a linear-elastic behavior. The modulus of elasticity is among the abbreviations Modulus of elasticity or as a formula symbol E. in the Spring calculation known; it has the unit “N / mm²” of mechanical stress.
The more resistance a material opposes its elastic deformation, the greater the amount of the Modulus of elasticity . A component made of a material with a high modulus of elasticity (for example spring steel) is thus stiffer than a component of the same construction (with identical geometric dimensions) made of a material with a low modulus of elasticity (for example rubber). The modulus of elasticity is the constant of proportionality in Hooke’s law .
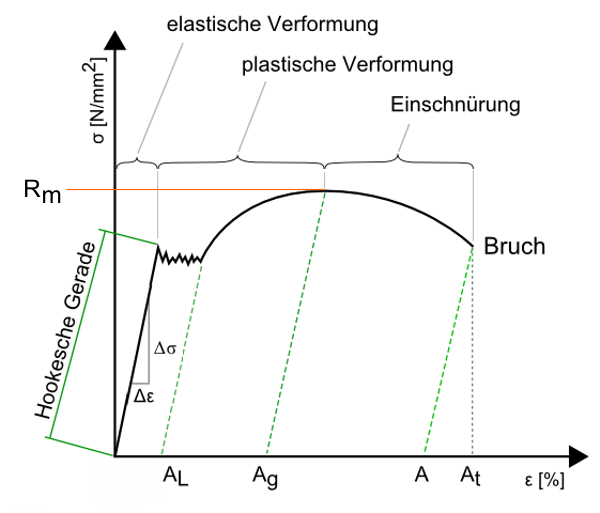
Rm = tensile strength
σ = stress
AL = Lüders expansion
Ag = uniform elongation
A = elongation at break
At = total elongation at break
Ɛ = elongation
The definition of the modulus of elasticity: The modulus of elasticity is the slope of the graph in the stress-strain diagram with uniaxial loading within the linear elasticity range. This linear area is also called Hooke’s straight line .
Here designated
σ = F / A (= force / area) die mechanical tension ( Normal stress , Not Shear stress ) and Ɛ = ∆L / L0 the expansion. The expansion is the ratio of the change in length ∆L = L – L0 to the original length L0
E – modulus of elasticity
σ – tension
ε – strain
There is that here modulus of elasticity for spring calculation at room temperature (20 ° C) for the most important spring materials.
However, the modulus of elasticity is not constant with regard to all physical quantities. So also influence the different environmental influences, such as temperature or Humidity , the modulus of elasticity. The adjustment of the modulus of elasticity is determined at higher temperatures using the following formula, where the Spring material parameters serve as a basis at room temperature (20 ° C).
For the interpretation of a suitable Compression- , Extension- or Torsion spring please contact our technical department directly by phone (+49) 035 877 227-13 or service@gutekunst-co.com .
For more information: