Hookesches Gesetz beschreibt die elastische Verformung von Festkörpern in einem linearen Sonderfall des Elastizitätsgesetzes. Dabei verändert sich die elastische Kraft des Körpers mit dem Ausdehnen oder dem Zusammendrücken. Bei der Anwendung von Druckfedern, Zugfedern und Schenkelfedern mit zylindrischer Bauform besteht ein linearer Zusammenhang zwischen Ausdehnung und Kraft. Dieses linear-elastische Verhalten von Festkörpern wird als Hookesches Gesetz bezeichnet, benannt nach dem englischen Gelehrten Robert Hooke.
Durch eine andere Gestaltung – wie durch einen geänderten Windungsdurchmesser oder Windungsabstand – lassen sich Metallfedern auch mit einer nicht linearen Verformung, bzw. Kraft-Weg-Verhältnis herstellen. Grundsätzlich beschreibt Hookesches Gesetzt die Aufgabe einer Metallfeder: Je länger die Strecke „s“ ist, um die eine Metallfeder gedehnt oder zusammengedrückt wird, desto stärker ist die entgegenwirkende Federkraft „F“ der Feder. Verformungen wie bei Gummi, oder die plastische Verformung bei Metallfedern nach Überschreiten der Proportionalitätsgrenze „Rp“ gehören nicht zum linearen Sonderfall des Elastizitätsgesetzes.
Table of Contents
Formel Hookesches Gesetz Metallfedern
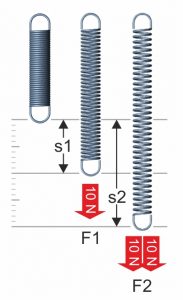
Das hookesche Gesetz besagt, dass der Federweg „s“ linear von der einwirkenden Kraft „F“ abhängt.
Formel Hookesches Gesetz: R=\frac{F}{s}
In der Formel des Hookeschen Gesetz dient die Federkonstante „R“ hierbei als Proportionalitätsfaktor und beschreibt die Steifigkeit der Metallfeder. Bei einer Zugfeder zeigt sich das lineare Verhalten bei Belastung mit einem Gewicht. Nach Verdoppelung des Gewichts tritt auch der doppelte Weg „s“ auf.
Diese Eigenschaft ist maßgeblich zum Beispiel für die Anwendung von Metallfedern als Kraftspeicher, Rückstellkraft, Lastverteilung und bei kraftschlüssigen Verbindungen wichtig. Bei anderen Materialien – wie zum Beispiel Gummi – ist der Zusammenhang zwischen einwirkender Kraft und Ausdehnung nicht linear.
Die Federkonstante
Die Federkonstante oder Federrate „R“ ist abhängig vom Werkstoff und der Bauform der Feder. Mit zunehmender Stärke oder einer engeren Wicklung des verwendeten Drahtes nimmt die Federkonstante einer Schraubenfeder zu. Sie wird in der Einheit Newton pro Millimeter (N/mm) angegeben und ist der Quotient aus der Federkraft „F“ und dem Federweg „s“:
R=\frac{F}{s}
Dabei gilt:
F = Federkraft [N]
R = Federrate / Federkonstante [N/mm]
s = Federweg [mm]
Berechnung der Federkraft:
Die Federkraft kann mit der folgenden Formel berechnet werden:
F=-R\cdot s
Dabei gilt:
F = Federkraft [N]; R = Federrate / Federkonstante [N/mm]; s = Federweg [mm]
Wieso ist die Federkonstante negativ? Das Minuszeichen in der Gleichung bedeutet, dass – bezogen auf die Ruhelage – die Auslenkungsrichtung einer Feder der Federkraft entgegengesetzt ist.
Die Formel für Federkraft wird nicht nur bei Druckfedern, Zugfedern und Schenkelfedern eingesetzt, sondern auch für andere elastische Körper. Ein wichtiges Thema ist die Federkraft daher unter anderem in der Mechanik und Werkstofftechnik.
Bei Bedarf an Druck-, Zug- oder Schenkelfedern senden Sie uns einfach unter verkauf@gutekunst-co.com die Daten der benötigten Metallfeder mit Angabe der Stückzahl und der Zeichnung. Wir erstellen Ihnen kurzfristig ein unverbindliches Angebot. Für weitere Informationen wenden Sie sich bitte direkt an unsere Technikabteilung unter Telefon (+49) 035877 227-13.
Weitere Informationen:
Beanspruchungsarten Druckfedern
Kugelstrahlen von Metallfedern
Federrate berechnen bei zylindrischen Federn
Federnshop von Gutekunst Federn