Di seguito è riportato il riepilogo delle nozioni di base su Design primaverile di Molle a compressione , Molle di tensione e Molle per le gambe .
Le molle tecniche sono ancora oggi uno degli elementi più importanti della macchina e vengono utilizzate con successo in veicoli, dispositivi meccanici o elettrotecnici di precisione, dispositivi medici, elettrodomestici e molto altro ancora. La funzione dell’intero dispositivo o parte della macchina dipende spesso dal funzionamento senza problemi della molla metallica.
Le molle metalliche sono elementi che deliberatamente si deformano sotto carico e tornano alla loro forma originale quando il carico viene rimosso. L’energia fornita è in Lavoro primaverile (W) convertito e rilasciato nuovamente in un secondo momento (riserva di energia). Tuttavia, le molle metalliche eseguono in modo affidabile questa deformazione e assorbimento di energia solo entro i limiti progettati per questo scopo. Quindi è quello giusto Design primaverile e Calcolo della primavera un componente importante per la molla metallica perfettamente funzionante.
Table of Contents
La curva caratteristica della molla
Molle metalliche o molle tecniche sono realizzate secondo il vostro Caratteristica della primavera giudicato. Questa caratteristica primaverile rappresenta la dipendenza del Forza della molla (F) rappresenta la corsa della molla. Perché a seconda di quale caratteristica della molla è richiesta (lineare, progressiva, decrescente o combinata), cambia anche la forma e il tipo di molla.
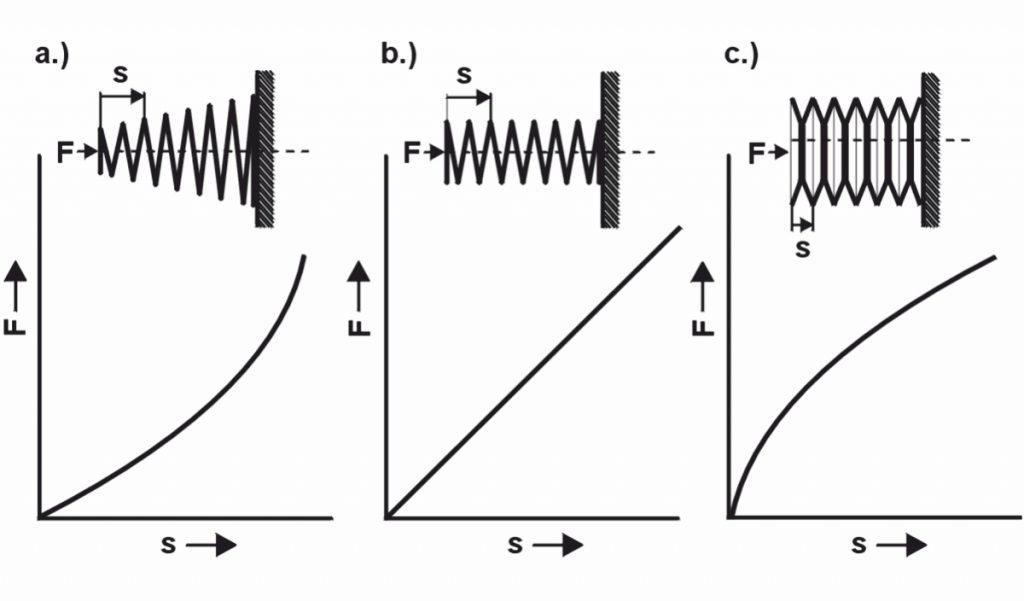
Con il Indice di rigidezza (R) la caratteristica della molla è determinata nel diagramma della molla. La rigidità della molla (R) è quindi un valore importante quando si progetta la molla per la molla giusta. A caratteristica molla lineare la rigidità della molla è costante. Le molle con una caratteristica della molla curva hanno una velocità della molla variabile. Le seguenti formule si applicano quindi a una caratteristica lineare:
per molle a compressione e trazione
R=\frac{F2-F1}{s2-s1}per molle di gamba e di torsione
R_{M}=\frac{M2-M1}{\alpha2-\alpha1}
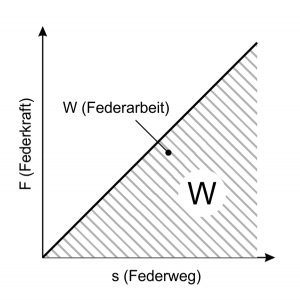
Il lavoro primaverile
Quando la molla metallica è in tensione, il lavoro è fatto, che viene poi rilasciato di nuovo quando la tensione viene rilasciata. Il lavoro della molla (W) risulta sempre come l’area al di sotto della caratteristica della molla. Con una caratteristica della molla lineare, vale quanto segue:
per molle a compressione e trazione
W=\frac{1}{2}F\cdot sper molle di gamba e di torsione
W=\frac{1}{2}M\cdot \alphaCalcolando il valore di utilità del volume, diversi tipi di molle possono essere determinati utilizzando il rapporto di lavoro della molla (W) e spazio di installazione (V) confrontare tra loro:
\eta_{A}=\frac{W}{V}
L’isteresi
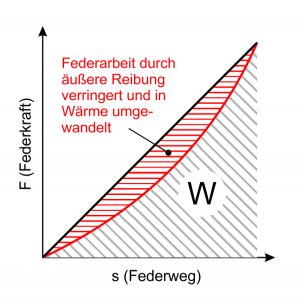
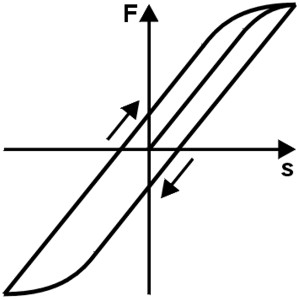
Il comportamento della sospensione può essere influenzato dall’attrito esterno. Queste forze di attrito ostacolano il recupero della molla. Nel caso di carichi alternati, questo è espresso sotto forma di a Ciclo di isteresi . Parte del lavoro della molla viene convertito in calore dall’attrito e quindi “perso”. Poiché ciò non è desiderabile quando si utilizzano molle, qualsiasi attrito deve essere progettato mediante disposizione e Forma delle piume essere evitato.
Il relax
Ad esempio, se viene utilizzata una molla di compressione temperatura più alta è compresso a una certa lunghezza tra piastre parallele, si può determinare che il file Forza della molla diminuisce gradualmente nel tempo. Questa perdita di forza aumenta con l’aumentare della temperatura e della tensione.
Rilassamento del materiale è una deformazione plastica che si manifesta come perdita di forza con una lunghezza di installazione costante. Questo è dato come percentuale della forza di uscita F1:
Rilassamento=\frac{\Delta F\cdot 100}{F1}Il diagramma seguente mostra il corso base del rilassamento e la velocità di rilassamento:
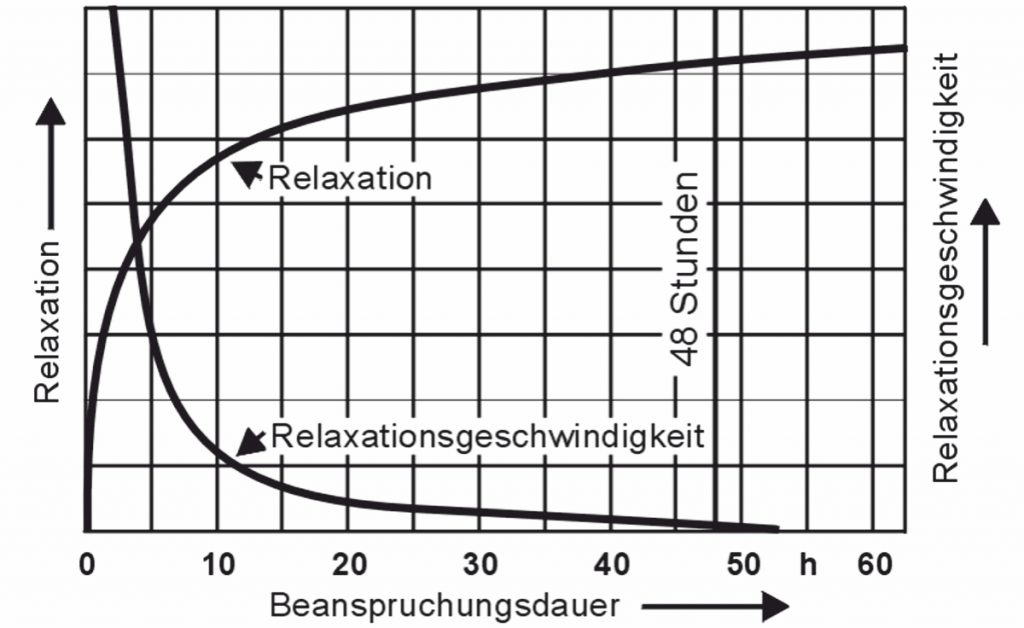
I valori di rilassamento dopo 48 ore sono considerati valori caratteristici, sebbene il rilassamento non sia ancora completamente completo in questo momento. I diagrammi di rilassamento dipendenti dal materiale possono essere trovati nella EN 13906-1. Questi devono essere inclusi dal progettista solo se sono poste elevate esigenze sulla costanza della forza della molla. Il rilassamento a diversi stati di temperatura viene utilizzato nel calcolo in Programma di calcolo della primavera WinFSB di Gutekunst Federn, disponibile all’indirizzo www.federnshop.com , mostrato con.
La giusta scelta del materiale della molla
Le molle metalliche devono essere prodotte con un materiale adatto e devono essere progettate e modellate in modo tale da ritornare alla loro forma originale dopo la rimozione del carico applicato. Questa proprietà è espressa in modulo di elasticità e nel modulo scorrevole. Queste Parametri del materiale esprimere la relazione tra tensione e allungamento e dovrebbe avere un valore il più alto possibile.
Inoltre, i materiali primaverili dovrebbero:
- limiti di elasticità elevati, ovvero un ampio intervallo puramente elastico,
- le tensioni corrispondenti anche a Temperature elevate sopportare senza una grande perdita di forza (basso rilassamento),
- hanno un’elevata resistenza alla fatica (struttura a grana fine, priva di impurità),
- avere una deformabilità sufficiente,
- avere una superficie il più scivolosa possibile,
- resistere a determinati requisiti per la protezione dalla corrosione,
- essere elettricamente conduttivo o non magnetico.
Elasticità e moduli di scorrimento di vari materiali per molle
| Materiale primaverile | Modulo di elasticità [N/mm²] | Modulo G. [N/mm²] |
| Filo di acciaio per molle trafilato brevettato secondo EN 10270-1 | 206000 | 81500 |
| Filo della molla della valvola temperato in olio secondo EN 10270-2 | 206000 | 81500 |
| Acciaio laminato a caldo secondo EN10089 | 206000 | 78500 |
| Nastri laminati a freddo secondo EN 10132 | 206000 | 78500 |
| X10 CrNi 18 8 (1.4310) | 185000 | 70000 |
| X7 CrNiAl 17 7 (1.4568) | 195000 | 73000 |
| X5 CrNiMo 17-12-2 (1.4401) | 180000 | 68000 |
| CuSn6 R950 secondo EN 12166 | 115000 | 42000 |
| CuZn36 R700 secondo EN 12166 | 110000 | 39000 |
| CuBe2 secondo EN 12166 | 120000 | 47000 |
| CuNi18Zn20 secondo EN 12166 | 135000 | 45000 |
| CuCo2Be secondo EN 12166 | 130000 | 48000 |
| Inconel X750 | 213000 | 76000 |
| Nimonic 90 | 213000 | 83000 |
| Hastelloy C4 | 210000 | 76000 |
| Lega di titanio TiAl6V4 | 104000 | 39000 |
Influenza della temperatura di lavoro sulla scelta del materiale delle molle
Comportamento a temperature di lavoro elevate
Il livello della temperatura di lavoro può influenzare in modo significativo la funzione di una molla, poiché la tendenza al rilassamento aumenta con l’aumentare della temperatura. Dopo aver valutato i diagrammi di rilassamento, è possibile impostare le seguenti temperature limite per i materiali primaverili più importanti.
Limita le temperature dei materiali primaverili con il minimo relax
| Materiale primaverile | Temperatura massima di esercizio in ° C a | |
| carico elevato | basso carico | |
| Filo di acciaio per molle trafilato brevettato secondo EN 10270-1 | 60-80 | 80-150 |
| Filo della molla della valvola temperato in olio secondo EN 10270-2 | 80-160 | 120-160 |
| X10CrNi 18,8 (1,4310) | 160 | 250 |
| X7CrNiAl 17,7 (1.4568) | 200 | 350 |
| X5CrNiMo 17-12-2 (1.4401) | 160 | 300 |
| CuSn6 | 80 | 100 |
| CuZn36 | 40 | 60 |
| CuBe2 | 80 | 120 |
| CuNi18Zn20 | 80 | 120 |
| Inconel X750 | 475 | 550 |
| Nimonic90 | 500 | 500 |
Inoltre, prendi l’importante per la funzione molla Proprietà dei materiali modulo di elasticità e il modulo di taglio diminuisce con l’aumentare della temperatura. Sia il modulo di taglio che il modulo di elasticità sono determinati a una temperatura più elevata utilizzando la seguente formula, con i parametri del materiale a temperatura ambiente (20 ° C) che servono come base.
G_{t}=G_{20}=\frac{3620-T}{3600}o.
E_{t}=E_{20}=\frac{3620-T}{3600}
Ciò consente al progettista di determinare le forze effettive della molla alla temperatura di esercizio prevista.
Comportamento a basse temperature di esercizio
Se utilizzato nei sistemi di raffreddamento, nello spazio o quando fa molto freddo in inverno, si devono sopportare temperature fino a – 200 °. Nonostante l’aumento resistenza alla trazione le basse temperature hanno un effetto sfavorevole, poiché la tenacità dei materiali diminuisce e possono verificarsi fratture fragili. Gli acciai per molle inossidabili così come le leghe di rame e nichel sono preferibili ai fili per molle brevettati e ai fili per molle delle valvole quando utilizzati a basse temperature. La tabella seguente mostra le temperature limite.
Raccomandazioni per l’uso a basse temperature
| Materiale primaverile | Temperatura minima di esercizio in ° C |
| Filo di acciaio per molle trafilato brevettato secondo EN 10270-1 | -60 |
| Filo della molla della valvola temperato in olio secondo EN 10270-2 | -60 |
| X10CrNi 18,8 (1,4310) | -200 |
| X7CrNiAl 17,7 (1.4568) | -200 |
| X5CrNiMo 17-12-2 (1.4401) | -200 |
| CuSn6 | -200 |
| CuZn36 | -200 |
| CuBe2 | -200 |
| CuNi18Zn20 | -200 |
| Inconel X750 | -100 |
| Nimonic90 | -100 |
Uso di sistemi a molla
Per motivi strutturali, è anche possibile utilizzare più molle per assorbire forze e movimenti. Semplice Sistemi a molla siamo Parallelo – e Collegamenti in serie .
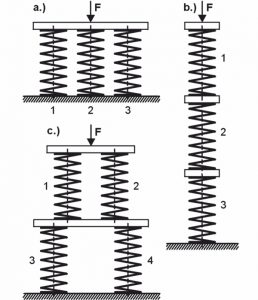
un) Connessione parallela
Le molle sono disposte in modo tale che il carico esterno (F) sia ripartito proporzionalmente tra le singole molle, ma la corsa delle singole molle è la stessa. Quindi risulta:
s=s1=s2=s3=... (corsa totale della sospensione) F=F1+F2+F3+... (forza totale della molla) R=R1+R2+R3+... (molla totale)La rigidità della molla del sistema complessivo di un collegamento in parallelo è sempre maggiore della rigidità delle singole molle
b) Collegamento in serie
Le molle sono disposte una dietro l’altra, in modo che la stessa forza agisca su ciascuna molla, ma la corsa della molla è divisa tra le singole molle. Risulta:
s=s1+s2+s3+... (corsa totale della sospensione) F=F1=F2=F3=... (forza totale della molla) R=\frac{1}{\frac{1}{R1}+\frac{1}{R2}+\frac{1}{R3}+...} (Indice di primavera totale)La rigidità della molla del sistema complessivo di una connessione in serie è sempre inferiore alla rigidità delle singole molle
c) Circuito misto
Diverse molle sono collegate in parallelo e una dietro l’altra. A causa dell’equilibrio, R1 = R2 e R3 = R4 devono essere. Nel caso mostrato, vale quanto segue:
R=\frac{1}{\frac{1}{R1+R2}+\frac{1}{R3+R4}+...} (Indice di primavera totale)La rigidità della molla del sistema complessivo del circuito di miscelazione mostrato è compresa tra la più piccola e la massima rigidità delle singole molle!
Nella seconda parte della serie di informazioni “ Progettazione di molle metalliche – Parte 2 “Calcolo “ti forniamo i parametri di calcolo per il Funzione e verifica della forza il Molle a compressione , Molle di tensione e Molle per le gambe di fronte.
Se hai bisogno di un progetto di molla personalizzato, è sufficiente inviarci via e-mail i dati chiave della molla metallica che desideri a service@federnshop.com, contattare telefonicamente il nostro ufficio tecnico al numero (+49) 035877 227-11 o utilizzare il programma di calcolo delle molle di Gutekunst WinFSB all’indirizzo www.federnshop.com per calcolare gratuitamente molle a compressione, molle a trazione e molle a torsione.
Informazioni aggiuntive: