Charakterystyka sprężyny pokazuje, jak metalowa sprężyna zachowuje się w pracy. Opisuje zależność między siłą sprężyny ( F ) i ugięcie sprężyny ( s ). W zależności od typu sprężyny lub zastosowanego systemu sprężyn rozróżnia się liniowe ( b ), progresywne ( a ), degresywne ( c ) lub kombinowaną charakterystykę sprężyny.
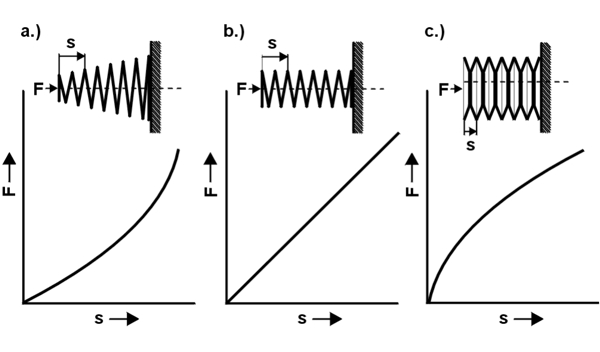
Progresywna charakterystyka sprężyny ( a ), który zwiększa siłę wraz ze wzrostem ugięcia, uzyskuje się za pomocą a stożkowa konstrukcja sprężyny i jednym mieszany obwód pojedynczej sprężyny n. Liniowa charakterystyka sprężyny ( b ), który równomiernie uwalnia siłę wraz ze wzrostem kompresji, uzyskuje się za pomocą konstrukcja cylindryczna i jednym rząd lub połączenie równoległe . Degresywna charakterystyka sprężyny ( c ), który zmniejsza siłę wraz ze wzrostem kompresji, można uzyskać za pomocą kolumna sprężyny talerzowej .
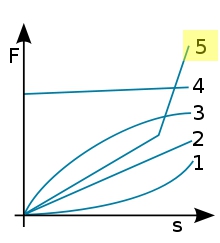
Połączona charakterystyka sprężyny ( 5 ), który gwałtownie zmienia właściwości siły w określonych stanach ściskania, można osiągnąć za pomocą kombinacji konstrukcji sprężyn i specjalnych wydziwianie – lub obiegi mieszaczy można osiągnąć za pomocą pojedynczych sprężyn. Charakterystyka sprężyny ( 4 ), z dużą siłą napięcia wstępnego i krzywą małej siły, uzyskuje się za pomocą miękkiej sprężyny wstępnie obciążonej
Sztywność ( R ) to nachylenie charakterystyki sprężyny na wykresie sprężyny. Przy liniowej charakterystyce sprężyny sztywność sprężyny jest stała. Sprężyny o zakrzywionej charakterystyce sprężyny mają zmienną sztywność. W przypadku liniowej charakterystyki sprężyny obowiązuje:
Ze sprężynami naciskowymi i naciągowymi
Ze sprężynami skrętnymi / sprężynami skrętnymi
Po więcej informacji:
- Obliczenie całkowitej sztywności sprężyny w równolegle -, wydziwianie – i obiegi mieszaczy