Design de molas metálicas – Parte 2 “Cálculo › Gutekunst Federn › Cálculo da mola, Druckfedern, Fórmulas, Fórmulas de cálculo, Schenkelfedern, Zugfedern

Na primeira parte desta série de duas partes, o Gutekunst Federn informou sobre os conceitos básicos do design de molas. Nesta segunda parte você encontrará os dados do cálculo concreto para o projeto de molas de compressão, molas de extensão e molas de torção (molas de torção). O programa de cálculo da mola Gutekunst WinFSB também está disponível para programa de cálculo da mola Gutekunst WinFSB individual.

O objectivo da concepção de uma mola de compressão, de extensão ou de torção é encontrar a mola mais económica para a tarefa em questão, tendo em conta todas as circunstâncias, que também se enquadre no espaço disponível e atinja a vida útil necessária. Para além destas exigências de fabrico e material, o design correcto design é de particular importância.

O projetista deve compilar os seguintes requisitos:

1. tipo de carga (estática ou dinâmica)

2. vida útil

3. Temperatura de funcionamento

4. Meio ambiente

5. Forças necessárias e deflexões da mola

6. Espaço de instalação disponível

7. Tolerâncias

8. situação de instalação (encurvadura, suspensão transversal)

Cada desenho de mola consiste em duas fases:

Comprovação do funcionamento: Verificação da velocidade da mola, das forças e do curso da mola, do comportamento de vibração, etc.
Verificação da resistência: Verificar a conformidade com as tensões permitidas ou a verificação da resistência à fadiga.

Isto requer uma abordagem iterativa.

A verificação da resistência é baseada na decisão se a mola está sujeita a uma carga estática, quase-estática ou dinâmica. Os seguintes critérios devem ser utilizados para a delimitação:

Cargaestática ou quase-estática: carga temporalmente constante (estática) ou carga temporalmente variável com menos de 10000 cursos no total.
Tensão dinâmica: cargas variáveis no tempo com mais de 10000 golpes. A mola é normalmente pré-carregada e sujeita a uma carga periódica de inchaço com uma curva sinusoidal, que ocorre de forma aleatória (estocasticamente), por exemplo, nas suspensões dos carros. Em alguns casos, ocorrem mudanças abruptas em força.

Ao dimensionar molas, devem ser especificados limites de carga que se baseiam nos valores de resistência dos materiais e levam em conta o tipo de carga. Para este efeito, está incluído um factor de segurança para determinar a tensão admissível. Após uma comparação com a tensão real existente, o dimensionamento da mola deve ser revisto por um procedimento iterativo. Aplica-se o seguinte:

Tensão nominal ≤ tensão admissível

Table of Contents

Cálculo de molas de compressão

Geral

As molas de compressão cilíndricas com passo constante são mais comumente usadas na prática. O fio é formado a frio, enrolando-o em torno de um mandril. Dependendo da alimentação do pino ascendente, o espaçamento da bobina e o contato da mola são regulados. Após o enrolamento, a mola é temperada a fim de reduzir as tensões residuais na mola e aumentar o limite de elasticidade de cisalhamento. O montante estabelecido é, portanto, reduzido. A temperatura e o tempo de resfriamento dependem do material; o resfriamento ocorre em ar à temperatura ambiente normal.

Outras operações importantes na produção de molas são a moagem e o ajuste. As extremidades das molas são normalmente retificadas a partir de uma espessura de arame de 0,5 mm para garantir um rolamento plano-paralelo da mola, bem como uma ótima transmissão de força.

Se a tensão de corte exceder o valor admissível quando a mola é carregada, ocorre uma deformação permanente, que é expressa na redução do comprimento não tensionado. Este processo é chamado de “cenário” na tecnologia de mola, que é equivalente aos termos “rastejar” e“relaxar” da tecnologia de materiais. Para contrariar isto, as molas de compressão são enroladas por mais tempo pela quantidade de ajuste esperada e posteriormente comprimidas para bloquear o comprimento. Esta pré-fixação permite uma melhor utilização do material e permite uma maior carga na utilização posterior.

Fórmula de cálculo mola de compressão cilíndrica

O cálculo da mola de compressão é baseado nas equações de cálculo da DIN EN 13906-1:

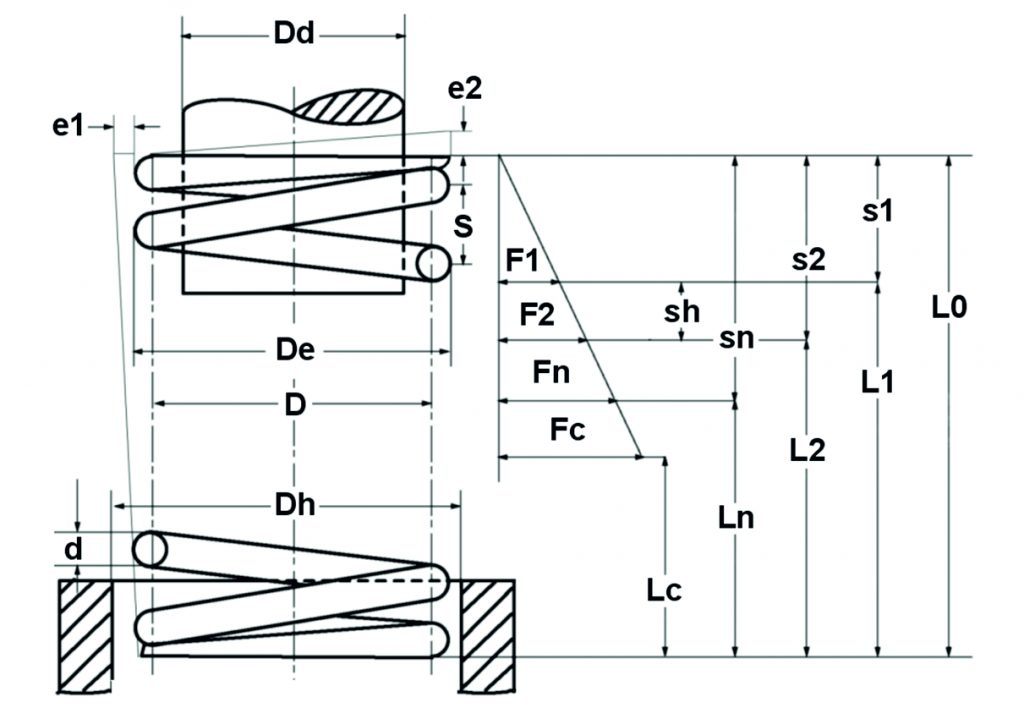
Figura: Diagrama de mola de compressão teórica

Comprovação do funcionamento das molas de compressão

O seguinte aplica-se a molas de compressão cilíndricas feitas de arame com seção transversal circular:

Taxa de Primavera: $R=\frac{ Gd^}{8D^n}$

segue de R=F/s:

Força da mola: $F=\frac{ Gd^s}{8D^n}$

e..:

Viagens de Primavera: $s=\frac{8D^nF}{Gd^}$

Mola de compressão de verificação de resistência

Após as dimensões da mola terem sido determinadas, a verificação da resistência deve ser feita. Para este fim, a tensão de cisalhamento existente é determinada:

Tensão do poder: $\Tau=frac$

Tensão fora do caminho: $\Tau=frac$

Enquanto a tensão de cisalhamento τ deve ser usada para o projeto de molas com carga estática ou quase estática, a tensão de cisalhamento corrigida τk se aplica a molas com carga dinâmica. A distribuição da tensão de corte na secção transversal do fio de uma mola é desigual, a tensão mais elevada ocorre no diâmetro interno da mola. Com o fator de correção de tensão k, que depende da relação de enrolamento (relação entre o diâmetro médio e a espessura do fio) da mola, a tensão mais alta pode ser determinada aproximadamente. Para molas de compressão carregadas dinamicamente, o resultado é, portanto:

Tensão de corte corrigida: $\=k$

onde se segura para k (de acordo com Bergsträsser):

$k=frac{\frac+0.5}{\frac-0.75}$

Agora a comparação é feita com a tensão admissível. Isto é definido da seguinte forma:

Tensão admissível:

$\{}=0.5 {{}$

$\{{czul}}=0.56 {\i1}cdot R_{{m}}$

Os valores para a resistência mínima à tração R_m dependem da espessura do fio e podem ser encontrados nas normas para os materiais correspondentes.

Como regra geral, as molas de compressão devem poder ser comprimidas até o comprimento do bloco, portanto, a tensão admissível no comprimento do bloco t_czul deve ser levada em consideração.

No caso de tensão dinâmica, devem ser determinadas as tensões inferior e superior (t_k1 e t_k2) do curso correspondente. A diferença é a tensão do curso. Tanto a tensão superior como a tensão de elevação não devem exceder os valores admissíveis correspondentes. Estes podem ser encontrados nos diagramas de resistência à fadiga da EN 13906-1:2002. Se as tensões suportarem esta comparação, a mola é resistente à fadiga a um número limite de ciclos de carga de¹⁰⁷.

Relações geométricas para molas de compressão

Parâmetro da mola	Equação de cálculo
Número total de voltas	n_t = n + 2
Comprimento do bloco da mola do solo	L_c = n_t d_max
Comprimento do bloco da mola não-terra	L_c = (n_t + 1.5)d_max
Comprimento útil mais pequeno	L_n = L_c +S_a
Comprimento sem tensão	L₀ = L_n +s_n
Soma das distâncias mínimas entre os enrolamentos	$S_==esquerda (0.0015 {D^} + 0.1d {direita ){cdot n$
Aumento do diâmetro externo sob carga Gradiente	$\Triângulo D_=0,1\frac{S^-08Sd-0,2d^}$ $S=\frac$ (terra) $S=\frac{L0-2,5d}{n}$ (não cortado)
Deflexão da mola de fivela (válida para diferentes coeficientes de rolamento n, ver EN 13906-1:2002)

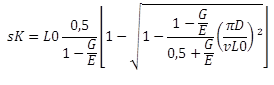Todas as molas dinamicamente tensionadas com uma espessura de arame > 1 mm devem ser remate peeningadas. Isto permite alcançar um aumento na força do curso contínuo. Após a verificação funcional e a verificação da resistência, vários cálculos geométricos devem ser efectuados e tidos em conta para poder encaixar a mola na construção do componente. O comprimento do bloco não pode ser inferior porque os enrolamentos estão bem conectados, o menor comprimento utilizável não deve ser inferior porque então uma curva de força linear, bem como a capacidade de carga dinâmica não são mais garantidas. Além disso, devem ser tidas em conta as tolerâncias admissíveis de acordo com a norma DIN 2095.

Cálculo da mola de tensão

Geral

Asmolas de extensão são enroladas ao redor de um mandril exatamente da mesma forma que as molas de compressão, mas sem espaçamento entre as bobinas e com diferentes formas de ilhós/pontas para a fixação da mola. Os enrolamentos são apertados firmemente juntos no processo de produção. Esta pré-carga interna F₀ depende da relação de enrolamento e não pode ser terminada a qualquer nível desejado. O software de cálculo WinFSB da Gutekunst Federn fornece valores de referência para a quantidade de pré-carga após a introdução dos respectivos dados da mola.

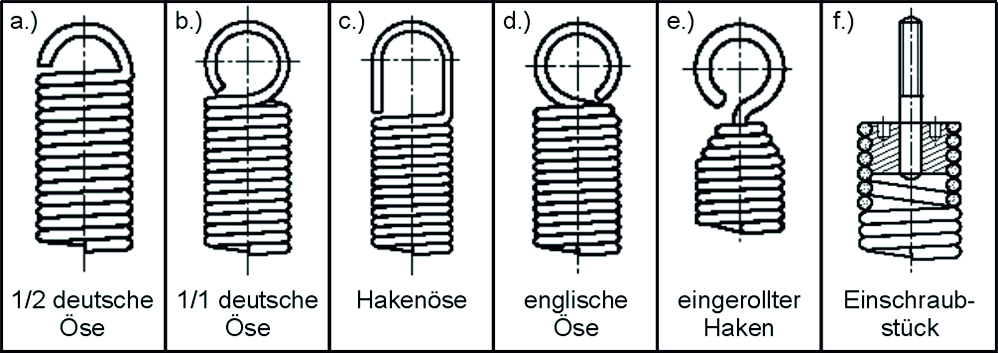
Imagem: Formas comuns de ilhós: a.) metade ilhós Alemão; b.) ilhós Alemão inteiro; c.) Olho de anzol; d.) ilhós inglês; e.) Gancho enrolado; f.) Peça aparafusada

A vantagem das molas de extensão é que elas não se dobram; a desvantagem é o maior espaço de instalação e a interrupção completa do fluxo de força no caso de ruptura da mola.

Fórmulas de cálculo mola de tensão cilíndrica

Correspondendo às equações de cálculo para molas de compressão, mas tendo em conta a força de pré-tensão, as seguintes relações aplicam-se a molas de tensão cilíndricas feitas de arame redondo (ver também a Figura 1.8):

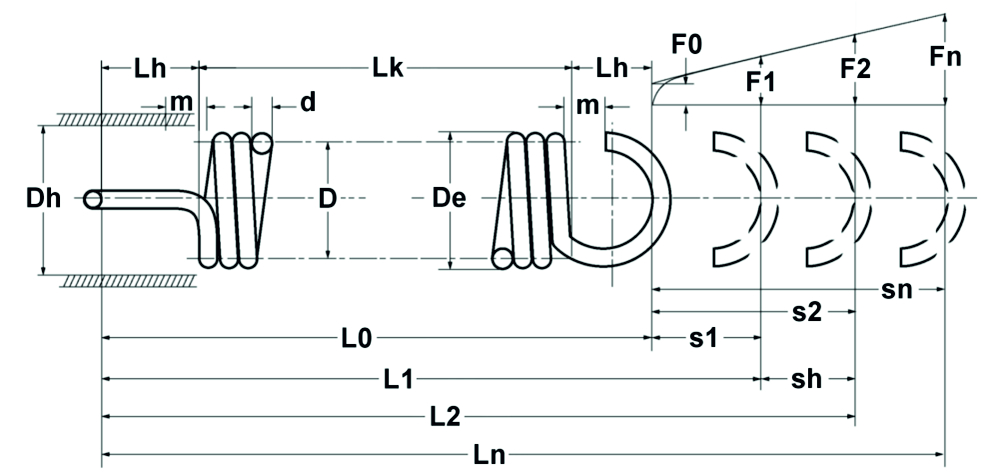
Figura: Diagrama de mola de tensão teórica

Prova funcional da mola de tensão

O seguinte aplica-se a molas de tensão cilíndricas feitas de arame com seção transversal circular:

Taxa de Primavera: $R=\frac{Gd^4}{8D^3n}=\frac$

segue de R=F/s:

Força da mola: $F=\frac{Gd^4s}{8D^3n}+F0$

e..:

Viagens de Primavera: $s=\frac{8D^3n(F-F0)}{Gd^4}$

Verificação da resistência das molas de tensão

Tal como nos cálculos das molas de compressão, a tensão de corte existente deve ser determinada.

Tensão de cisalhamento: $\Tau=frac$

Da mesma forma, a tensão de curso corrigida deve ser calculada para tensão dinâmica.

Tensão de corte corrigida: $\{ }=k=tau$

Tensão admissível: $\{ }=0.45 {{}$

A tensão máxima tn existente no maior curso de mola_sn é igual à tensão permitida. No entanto, para evitar o relaxamento, apenas 80% desta viagem de primavera deve ser usada na prática.

$s_{}=0.8 \cdot s_{}$

Não podem ser dados valores de resistência à fadiga geralmente válidos para tensões dinâmicas, pois podem ocorrer tensões adicionais nos pontos de flexão dos ilhós, algumas das quais podem exceder as tensões admissíveis. Portanto, as molas de tensão só devem ser sujeitas a cargas estáticas se possível. Se não for possível evitar tensões dinâmicas, devem ser evitados ilhós dobrados edevem ser utilizadas peças finais enroladas ou aparafusadas. Um teste de vida útil sob condições de uso posteriores faz sentido. O endurecimento da superfície por shot peening não é viável devido às bobinas muito espaçadas.

Relações geométricas para molas de tensão

Parâmetro da mola	Equação de cálculo
Comprimento do corpo	L_K = (n_t + 1)d
Comprimento sem tensão	L₀ = L_K + 2 L_H
Altura do ilhós meio ilhós Alemão	L_H = 0,55D_i a 0,80D_i
Altura do ilhós Alemão inteiro	L_H = 0,80D_i a 1,10D_i
Olho de anzol em altura	L_H > 1.10D_i
Altura dos olhos ilhós inglês	L_H = 1.10D_i

Devem ser tidas em conta as tolerâncias de fabrico permitidas de acordo com a norma DIN 2097.

Cálculo de molas de torção (molas de torção)

Geral

As molas de torção cilíndricas enroladas (molas de torção) têm essencialmente a mesma forma que as molas cilíndricas de compressão e extensão, mas com excepção das extremidades das molas. Estes são dobrados em forma de perna para permitir que o corpo da mola gire em torno do eixo da mola. Isto significa que existem muitas áreas diferentes de aplicação, por exemplo, como molas de retorno ou molas de dobradiça. A mola de torção deve ser montada em um mandril guia e a carga só deve ser aplicada na direção do enrolamento. O diâmetro interno é reduzido no processo. As molas são normalmente enroladas sem inclinação. No entanto, se o atrito for absolutamente indesejável, as molas de torção também podem ser fabricadas com espaçamento entre bobinas. Em caso de tensão dinâmica, certifique-se de que não existem curvas acentuadas nas extremidades das molas, a fim de evitar picos de tensão imprevisíveis.

Fórmulas de cálculo molas de torção cilíndricas (molas de torção)

O cálculo é efectuado de acordo com as directrizes da EN 13906-3:2001:

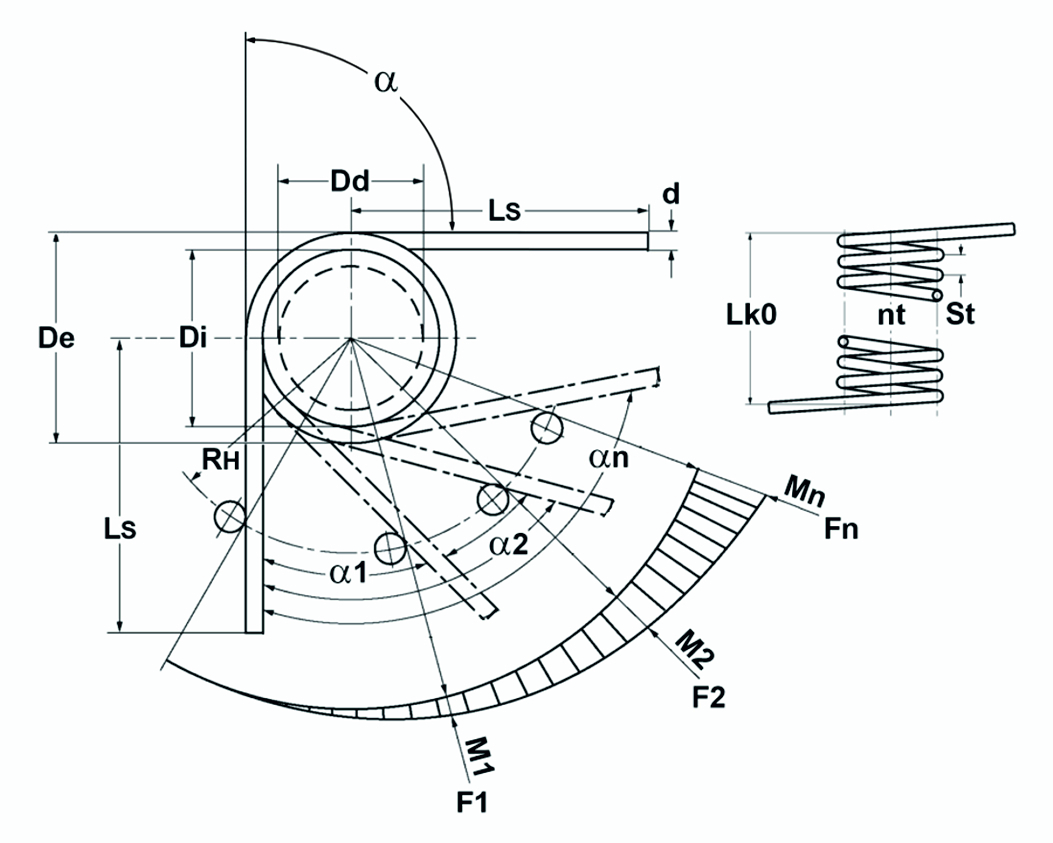
Figura: Diagrama de mola de torção teórica / mola de torção

Verificação funcional das molas de torção (molas de torção)

Feather Mom Rate: $R_=\frac{\alpha}=\frac{d^4E}$

Momento primaveril: $M=FR_=\frac{d^4E\alpha}$

Ângulo de rotação: $\Alpha=frac$

Verificação da resistência das molas de torção (molas de torção)

A tensão de flexão existente é determinada e comparada com a tensão admissível. No caso de tensão dinâmica, a tensão corrigida deve ser novamente utilizada para comparação.

Stress de flexão: $\Sigma=frac$

Correcção do stress de flexão: $\sigma_{}=q \sigma$

onde q está:

$q=frac{\frac+0.07}{\frac-0.75}$

Tensão de flexão permitida: $\sigma_{}=0.7Rm$

No caso de tensão dinâmica, devem ser determinadas as tensões inferior e superior (t_k1 e t_k2) do curso correspondente. A diferença é a tensão do curso. Tanto a tensão superior como a tensão de elevação não devem exceder os valores admissíveis correspondentes. Para arames de aço para molas, estes podem ser retirados dos diagramas de resistência à fadiga da EN 13906-3:2001. Se as tensões suportarem esta comparação, a mola é resistente à fadiga a um número limite de ciclos de carga de¹⁰⁷.

Relações geométricas para molas de torção (molas de torção)

Parâmetro da mola	Equação de cálculo
Redução do diâmetro interno na carga máxima	$Di_=\frac{n+frac{\alpha}}-d$
Comprimento do corpo descarregado	$Lk=(n+1,5)d$
Comprimento do corpo na condição de carga máxima	$Lk_=(n+1,5+\frac{\alpha})d$
Viagens de Primavera	$s_= \frac{\alpha_R_}{57,3}$

Além disso, devem ser consideradas as tolerâncias de fabrico de acordo com a norma DIN 2194.

Um resumo do artigo “Desenho de uma mola metálica”, que consiste na Parte 1 “Fundamentos” e na Parte 2 “Cálculo”, também pode ser baixado do Gutekunst Federn 1×1.

Se precisar de um desenho individual de mola, basta enviar-nos os dados chave da mola metálica necessária para technik@gutekunst-co.com, contactar o nosso departamento técnico pelo telefone (+49) 035877 227-11 ou utilizar o programa de cálculo de molas Gutekunst WinFSB em https://www.federnshop.com para cálculo gratuito de molas de compressão, molas de extensão e molas de torção.

Para mais informações:

Design de mola de compressão (vídeo)

Design de mola de tensão (vídeo)

Design de molas metálicas – Parte 1 “Noções básicas

Dados de medição para o desenho da mola

Programa de cálculo da Primavera WinFSB 8

Fios de aço de mola e suas propriedades

Design de molas metálicas – Parte 2 “Cálculo

Tagged on: Cálculo da mola Druckfedern Fórmulas Fórmulas de cálculo Schenkelfedern Zugfedern