Dans la première partie de cette série en deux parties, Gutekunst Federn a présenté les bases de la conception des ressorts. Dans cette deuxième partie, vous trouverez les données de calcul concrètes pour la conception des ressorts de compression, des ressorts de traction et des ressorts de tor sion (ressorts de torsion). Pour un calcul personnalisé, vous pouvez également utiliser le programme de calcul de ressorts de Gutekunst WinFSB.
L’objectif de la conception d’un ressort de compression, de traction ou de torsion est de trouver le ressort le plus économique pour la tâche donnée, en tenant compte de toutes les circonstances, qui s’adapte également à l’espace disponible et atteint la durée de vie requise. Outre ces exigences en matière de fabrication et de matériaux, la conception correcte du ressort revêt une importance particulière.
Avant de calculer le ressort, les exigences suivantes du ressort métallique doivent être rassemblées :
1. type de charge (statique ou dynamique)
2. À vie
3. Température de fonctionnement
5. Forces et débattements nécessaires
6. espace de montage disponible
7. tolérances(ressorts de compression, ressorts de traction)
8. situation de montage (flambage, suspension transversale)
Chaque calcul de ressort se compose de deux étapes :
- Vérification du fonctionnement: contrôle de la raideur du ressort, des forces et des débattements, du comportement vibratoire, etc.
- Contrôle de résistance
: vérification du respect des contraintes admissibles ou vérification de la résistance à la fatigue.
Pour ce faire, une approche itérative est nécessaire.
La vérification de la résistance est basée sur la décision de soumettre le ressort à une charge statique, quasi-statique ou dynamique. Les critères suivants doivent être utilisés pour la délimitation :
- Contrainte statique ou quasi-statique: charge constante dans le temps (au repos) ou charge variable dans le temps avec moins de 10000 courses au total.
- Sollicitation dynamique: charges variables dans le temps avec plus de 10000 courses. Le ressort est généralement précontraint et soumis à des charges de gonflement périodiques de forme sinusoïdale, qui se produisent de manière aléatoire (stochastique), par exemple dans les suspensions automobiles. Dans certains cas, il y a des changements brusques de force.
Lors du dimensionnement du ressort, il convient de définir des limites de sollicitation basées sur les valeurs de résistance des matériaux et tenant compte du type de sollicitation. Pour ce faire, un facteur de sécurité est inclus et la tension admissible est ainsi déterminée. Après une comparaison avec la contrainte réelle, le dimensionnement du ressort doit être révisé par une approche itérative. Tension nominale ≤ Tension admissible
Table des matières
Calcul des ressorts de compression
Généralités
Les ressorts de compression cylindriques à pas constant formés à froid sont les plus utilisés dans la pratique. Le fil est déformé à froid en étant enroulé autour d’un mandrin. L’espacement des spires et le contact du ressort sont réglés en fonction de l’avance de la broche de pas. Après le treuillage, on procède au revenu afin de réduire les contraintes résiduelles dans le ressort et d’augmenter la limite d’élasticité en cisaillement. Le montant de l’abattement est donc réduit. Les températures et les durées de revenu dépendent du matériau ; le refroidissement se fait à l’air à température ambiante normale.
D’autres opérations importantes dans la fabrication des ressorts sont le meulage et la composition. Les extrémités des ressorts sont généralement rectifiées à partir d’une épaisseur de fil de 0,5 mm afin de garantir un montage à faces planes du ressort ainsi qu’une transmission optimale des forces.
Si, lorsque le ressort est soumis à une charge, la contrainte de cisaillement dépasse la valeur admissible, une déformation permanente se produit, qui se traduit par une réduction de la longueur non tendue. Ce processus est appelé « tassement » dans la technologie des ressorts, ce qui est équivalent aux termes « fluage » et « relaxation » utilisés dans la technologie des matériaux. Pour y remédier, les ressorts de compression sont enroulés plus longuement de la valeur attendue du tassement et sont ensuite comprimés à la longueur du bloc. Cette avancée permet une meilleure utilisation du matériau et autorise une charge plus élevée lors de l’utilisation ultérieure.
Formules de calcul pour les ressorts de compression cylindriques
Le calcul du ressort de compression est basé sur les équations de calcul de la norme DIN EN 13906-1 :
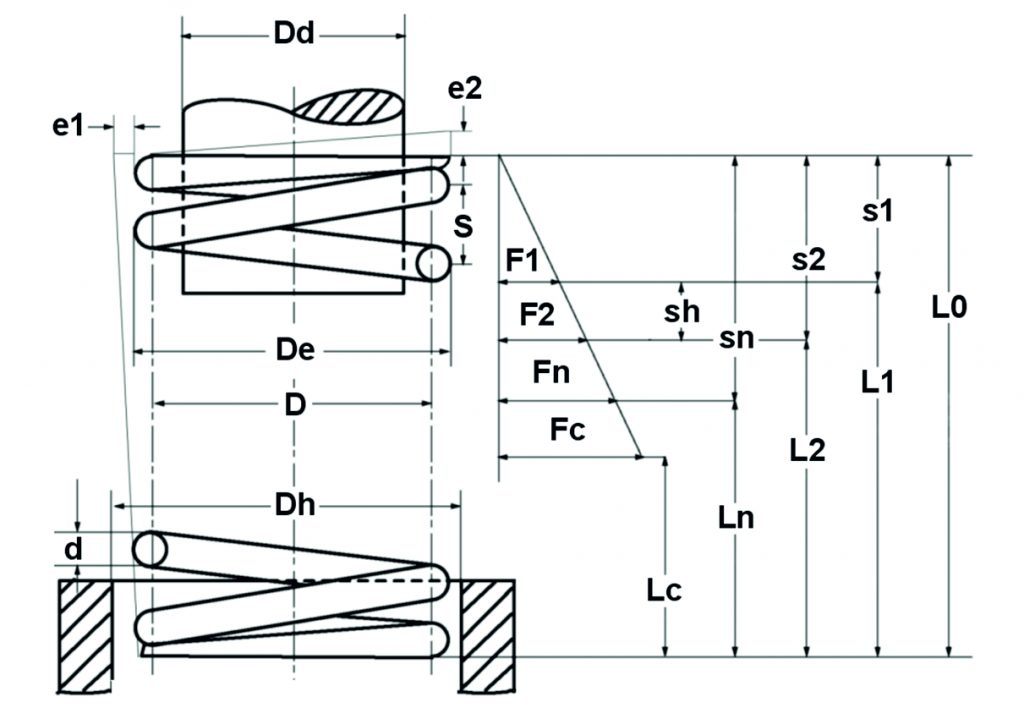
Figure : Diagramme théorique du ressort de compression
Preuve de fonctionnement des ressorts de compression
Pour les ressorts de compression cylindriques en fil de section circulaire, on a
Formule du taux de ressort : \Large R=\frac{ Gd^{4}}{8D^{3}n}
résulte de R=F/s :
Force du ressort : \Large F=\frac{ Gd^{4}s}{8D^{3}n}
ainsi que :
Voyage en suspension : \Large s=\frac{8D^{3}nF}{Gd^{4}}
Certificat de résistance du ressort de compression
Une fois les dimensions du ressort déterminées, la résistance doit être vérifiée. Pour ce faire, la contrainte de cisaillement existante est déterminée :
Tension à partir de la force : \Large \tau=\frac{8DF}{\pi d^{3}}
Tension hors du chemin : \Large \tau=\frac{Gds}{\pi n D^{2}}
Alors que la contrainte de cisaillement τ doit être utilisée pour la conception de ressorts soumis à des charges statiques ou quasi-statiques, la contrainte de cisaillement corrigée τk s’appliqueaux ressorts soumis à des charges dynamiques. La répartition de la contrainte de cisaillement dans la section transversale du fil d’un ressort est inégale, la contrainte la plus élevée se produit sur le diamètre intérieur du ressort. Avec le facteur de correction de tension k, qui dépend du rapport d’enroulement (rapport du diamètre moyen à l’épaisseur du fil) du ressort, la tension la plus élevée peut être approximativement déterminée. Pour les ressorts de compression soumis à des contraintes dynamiques, il en résulte donc :
Contrainte de cisaillement corrigée : \Large \tau_{k}=k\tau
où k est (selon Bergsträsser) :
\Large k=\frac{\frac{D}{d}+0,5}{\frac{D}{d}-0,75}Maintenant, la comparaison est faite avec la tension admissible. Ceci est défini comme suit:
Tension admissible:
\Large \tau_{{zul}}=0,5\cdot R_{{m}}und
\Large \tau_{{czul}}=0,56\cdot R_{{m}}Les valeurs duRésistance minimale à la traction R m dépendent de l’épaisseur du fil et peuvent être trouvés dans les normes des matériaux correspondants.
En règle générale, il doit être possible de comprimer les ressorts de compression jusqu’à la longueur du bloc, c’est pourquoi la contrainte admissible à la longueur du bloc est t czul à envisager.
En cas de sollicitation dynamique, les tensions inférieure et supérieure (tk1et tk2) de la course correspondante doivent être déterminées. La différence est la tension de course. La tension supérieure et la tension de course ne doivent pas dépasser les valeurs admissibles correspondantes. Celles-ci peuvent être trouvées dans les diagrammes de résistance à la fatigue de la norme EN 13906-1:2002. Si les contraintes résistent à cette comparaison, le ressort est résistant à la fatigue avec un cycle de charge limite de 10 7 .
Relations géométriques pour les ressorts de compression
| Taille caractéristique du ressort | Équation de calcul |
| Nombre total de spires | nt = n + 2 |
| Longueur du bloc du ressort rectifié | Lc = nt dmax |
| Longueur du bloc du ressort non rectifié | Lc = (nt + 1,5)dmax |
| Plus petite longueur utile | Ln = Lc +Sa |
| Longueur non tendue | L0 = Ln +sn |
| Somme des distances minimales entre les spires | \Large S_{a}=\left (0,0015 \frac{D^{2}}{d} + 0,1d \right )\cdot n |
| Augmentation du diamètre extérieur en cas de charge
terrain |
\Large \triangle D_{e}=0,1\frac{S^{2}-08Sd-0,2d^{2}}{D}
\Large S=\frac{L0-d}{n} (poncé) \Large S=\frac{L0-2,5d}{n} (non rectifié)
|
|
Course du ressort de flambage (valable pour différents coefficients d’appui n, voir EN 13906-1:2002) |
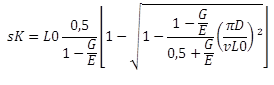 |
Tous les ressorts soumis à des contraintes dynamiques avec une épaisseur de fil > 1 mm doivent être grenaillés. Il est ainsi possible d’obtenir une augmentation de la résistance à la course d’endurance. Une fois que la vérification fonctionnelle et la vérification de la résistance ont été effectuées, différents calculs géométriques doivent être réalisés et pris en compte afin d’intégrer le ressort dans la construction de l’élément de construction. Il n’est pas possible de descendre en dessous de la longueur du bloc, car les spires sont fixes les unes par rapport aux autres. Il ne faut pas descendre en dessous de la plus petite longueur utilisable, car dans ce cas, une courbe de force linéaire et une capacité de charge dynamique ne sont plus garanties. En outre, les tolérances admissibles selon la norme DIN 2095 doivent être prises en compte.
Calcul des ressorts de traction
Généralités
Les ressorts de traction sont enroulés autour d’un mandrin, tout comme les ressorts de compression, mais sans espacement des spires et avec différentes formes d’œillets/extrémités de ressort pour fixer le ressort. Les spires sont alors étroitement pressées les unes contre les autres par la technique de fabrication. Cette précontrainte interne F0 dépend du rapport d’enroulement et ne peut pas être terminée à n’importe quelle hauteur. Le logiciel de calcul WinFSB de Gutekunst Federn fournit des valeurs indicatives pour la valeur de la précontrainte après l’entrée des données du ressort concerné.
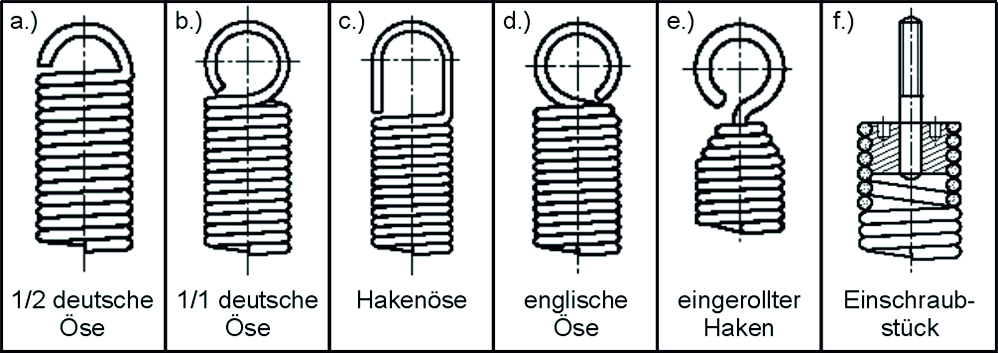
Image : Formes d’œillets les plus courantes : a.) demi-œillet allemand ; b.) Œillet allemand entier ; c.) Œillet de crochet ; d.) œillet anglais ; e.) crochet enroulé ; f.) Pièce à visser
L’avantage des ressorts de traction réside dans l’absence de flambage, l’inconvénient étant un espace de montage plus important et l’interruption complète du flux de force en cas de rupture du ressort.
Formules de calcul des ressorts de traction cylindriques
Conformément aux équations de calcul des ressorts de compression, mais en tenant compte de la force de précontrainte, les relations suivantes s’appliquent aux ressorts de traction cylindriques en fil rond (voir également Figure 1.8) :
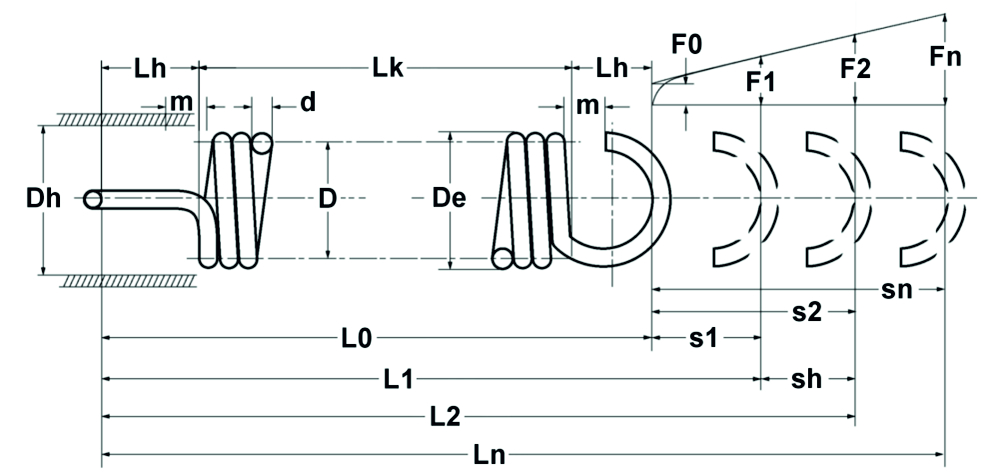
Figure : Diagramme théorique des ressorts de traction
Preuve de fonctionnement du ressort de traction
Pour les ressorts de traction cylindriques en fil de section circulaire, on a
Taux de ressort : \Large R=\frac{Gd^4}{8D^3n}=\frac{F-F0}{s}
résulte de R=F/s :
Force du ressort : \Large F=\frac{Gd^4s}{8D^3n}+F0
ainsi que :
Course du ressort : \Large s=\frac{8D^3n(F-F0)}{Gd^4}
Contrôle de résistance des ressorts de traction
Comme pour les calculs de ressorts de compression, la contrainte de cisaillement existante doit être déterminée.
Contrainte de cisaillement : \Large \tau=\frac{8DF}{\pi d^3}
De même, pour une sollicitation dynamique, la contrainte de levage corrigée doit être calculée.
Contrainte de cisaillement corrigée : \Large \tau_{{k}}=k\tau
Tension admissible : \Large \tau_{{zul}}=0,45 \cdot R_{{m}}
La tension maximale existante t n pour les plus grands déplacements n est égal à la tension admissible. Toutefois, pour éviter la relaxation, il convient en pratique de n’utiliser que 80 % de ce débattement.
\Large s_{{2}}=0,8 \cdot s_{{n}}Pour les sollicitations dynamiques, il n’est pas possible d’indiquer des valeurs de résistance à la fatigue universellement valables, car dans certaines circonstances, des tensions supplémentaires apparaissent aux points de flexion des œillets, qui peuvent parfois dépasser les tensions admissibles. Les ressorts de traction ne doivent donc être soumis, dans la mesure du possible, qu’à des contraintes statiques. Si le stress dynamique ne peut être évité, il faut opter pour un angle Oeillets se passer et utiliser des embouts roulés ou vissés. Un test de durée de vie dans des conditions de fonctionnement ultérieures a du sens. La consolidation de la surface par grenaillage n’est pas réalisable en raison de la proximité des spires.
Relations géométriques pour les ressorts de traction
| Taille caractéristique du ressort | Équation de calcul |
| Longueur du corps | LK = (nt + 1)d |
| Longueur non tendue | L0 = LK + 2 LH |
| Hauteur d’œillet demi-œillet allemand | LH = 0,55Di à 0,80Di |
| Hauteur de l’œillet entier allemand | LH = 0,80Di à 1,10Di |
| Hauteur de l’œillet Crochet | LH > 1,10Di |
| Hauteur de l’œillet anglais | LH = 1,10Di |
Les tolérances de fabrication autorisées par la norme DIN 2097 doivent être respectées.
Calcul des ressorts de torsion (ressorts de torsion)
Généralités
Les ressorts de torsion cylindriques enroulés (ressorts de torsion) ont essentiellement la même forme que les ressorts de compression et de traction cylindriques, à l’exception des extrémités du ressort. Ceux-ci sont pliés en forme de branche pour permettre la rotation du corps du ressort autour de l’axe du ressort. Il existe donc de très nombreuses applications différentes, par exemple comme ressorts de rappel ou ressorts de charnière. Le logement du ressort de torsion doit être effectué sur un mandrin de guidage et la charge doit être appliquée uniquement dans le sens de l’enroulement. Le diamètre intérieur diminue. Les ressorts sont généralement enroulés sans pente. Toutefois, si le frottement est absolument indésirable, les ressorts de torsion peuvent également être fabriqués avec un espacement des spires. En cas de sollicitation dynamique, il faut veiller à ce qu’il n’y ait pas de courbure à angle vif aux extrémités du ressort afin d’éviter les pics de tension imprévisibles.
Formules de calcul des ressorts de torsion cylindriques (ressorts de torsion)
Le calcul est effectué conformément aux directives de la norme EN 13906-3:2001 :
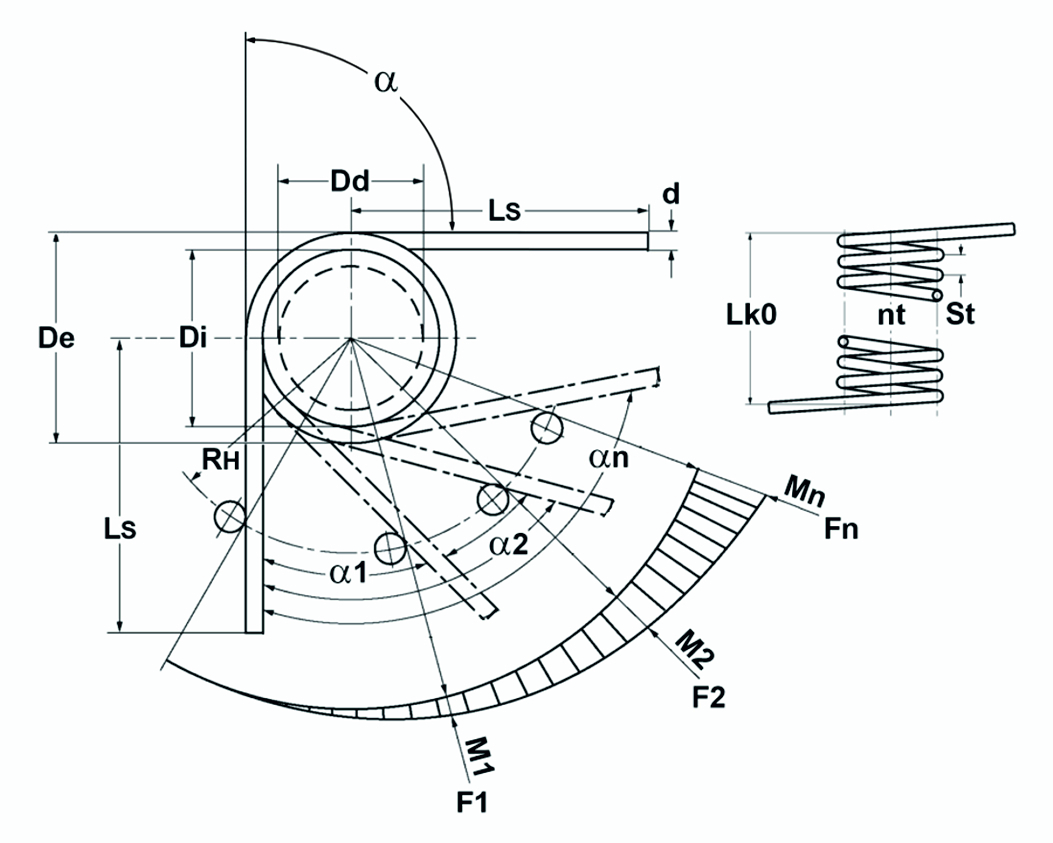
Figure : Diagramme théorique ressort de torsion/ressort de torsion
Justificatif de fonctionnement des ressorts de torsion (ressorts de torsion)
Taux de maternité à ressort : \Large R_{M}=\frac{M}{\alpha}=\frac{d^4E}{3667Dn}
Couple de ressort : \Large M=FR_{H}=\frac{d^4E\alpha}{3667Dn}
angle de rotation : \Large \alpha=\frac{3667DMn}{Ed^4}
Contrôle de résistance des ressorts de torsion
La contrainte de flexion existante est déterminée et comparée à la contrainte admissible. En cas de sollicitation dynamique, la contrainte corrigée doit à nouveau être utilisée pour la comparaison.
Tension de flexion : \Large \sigma=\frac{32M}{\pi d^3}
Contrainte de flexion corrigée : \Large \sigma_{{q}}=q \sigma
où q est
\Large q=\frac{\frac{D}{d}+0,07}{\frac{D}{d}-0,75}
Tension de flexion admissible : \Large \sigma_{{zul}}=0,7Rm
À contrainte dynamique la tension doit être inférieure et supérieure (t k 1 et t k 2) de la course correspondante peut être déterminée. La différence est la tension de course. La tension supérieure et la tension de course ne doivent pas dépasser les valeurs admissibles correspondantes. Pour les fils d’acier à ressorts, celles-ci sont indiquées dans les diagrammes de résistance à la fatigue de l’EN 13906-3:2001. Si les contraintes résistent à cette comparaison, le ressort est résistant à la fatigue avec un cycle de charge limite de 10 7 .
Relations géométriques pour les ressorts de torsion (ressorts de torsion)
| Taille caractéristique du ressort | Équation de calcul |
| Réduction du diamètre intérieur à la charge maximale | \Large Di_{n}=\frac{Dn}{n+\frac{\alpha}{360}}-d |
| Longueur du corps non chargée | \Large Lk=(n+1,5)d |
| Longueur du corps à l’état de charge maximale | \Large Lk_{n}=(n+1,5+\frac{\i1alpha}{360})d |
| Débattement de la suspension | \Large s_{n}= \frac{alpha_{n}R_{H}}{57,3} |
De plus, les tolérances de fabrication doivent être prises en compte conformément à la norme DIN 2194.
Vous trouverez également un résumé de l’article « Conception d’un ressort métallique », composé de la partie 1 « Principes de base » et de la partie 2 « Calcul », à télécharger dans le Gutekunst Federn 1×1.
Si vous avez besoin d’une conception de ressort individuelle, envoyez-nous simplement les données de référence du ressort métallique dont vous avez besoin par e-mail à technik@gutekunst-co.com, contactez notre service technique par téléphone au (+49) 035877 227-11 ou utilisez le programme de calcul de ressorts de Gutekunst WinFSB sur https://www.federnshop.com pour calculer librement les ressorts de compression, les ressorts de traction et les ressorts de torsion.
Information additionnelle: