V první části této dvoudílné série má Gutekunst peří o Základy pružinového designu informovaný. V této druhé části najdete konkrétní výpočtová data pro návrh Tlačné pružiny , Tažné pružiny a Pružiny nohou (Torzní pružiny). To je také k dispozici pro individuální výpočet Program výpočtu pružin Gutekunst WinFSB k likvidaci.

Cílem konstrukce pružiny tlačné pružiny, tažné pružiny nebo nožní pružiny je najít nejekonomičtější pružinu pro daný úkol s přihlédnutím ke všem okolnostem, která také zapadá do dostupného prostoru a která je požadována životnost dosáhl. Kromě těchto výrobních a materiálových požadavků existuje i ten pravý Jarní design zvláštní význam pro.

Návrhář by měl dát dohromady následující požadavky:

1. Typ zatížení (statické nebo dynamické)

2. životnost

3. Provozní teplota

4. Okolní médium

5. Potřebné síly a pojezd pružiny

6. Stávající instalační prostor

7. Tolerance

8. Situace instalace (Vzpěr, boční zavěšení)

 

Každý jarní design se skládá ze dvou fází:

  • Důkaz funkce : Kontrola pružiny, sil a dráhy pružiny, chování vibrací atd.
  • Důkaz síly : Zkontrolovat dodržení přípustných napětí nebo důkaz únavové pevnosti.

To vyžaduje iterativní přístup.

The Důkaz síly je založeno na rozhodnutí, zda je pružina zatížena staticky, kvazi-staticky nebo dynamicky. Pro vymezení by měla být použita následující kritéria:

  • Statické nebo kvazistatické napětí : Časově konstantní (klidové) zatížení nebo časově proměnné zatížení s celkovým počtem méně než 10 000 zdvihů.
  • Dynamický stres : časově proměnná zatížení s více než 10 000 zdvihy. Pružina je většinou předepnutá a vystavena periodickým bobtnáním se sinusovou křivkou, které se vyskytují náhodně (stochasticky), například v případě zavěšení vozidla. V některých případech dochází k náhlým změnám síly.

Při dimenzování pružin je třeba určit meze napětí, které vycházejí z Hodnoty pevnosti materiálů a vezměte v úvahu typ stresu. K určení přípustného napětí je zahrnut bezpečnostní faktor. Po srovnání se skutečným napětím musí být dimenzování pružiny revidováno pomocí iteračního postupu. Platí následující:

Jmenovité napětí ≤ přípustné napětí

Výpočet tlačných pružin

Všeobecné

Za studena válcové tlačné pružiny s konstantním sklonem se v praxi nejčastěji používají. Drát je za studena formován navinutím kolem trnu. V závislosti na posuvu stoupacího kolíku jsou regulovány rozteč cívky a poloha pružiny. Po navinutí proběhne popouštění, aby se snížilo vnitřní napětí na jaře a zvýšil se limit smykové pružnosti. Takže Nastavení částky . Popouštěcí teploty a doby závisí na materiálu; chlazení probíhá na vzduchu při normální pokojové teplotě.

Dalšími důležitými pracovními kroky při výrobě pružin jsou broušení a tuhnutí. Konce pružin jsou obvykle broušeny od tloušťky drátu 0,5 mm, aby bylo zajištěno rovnoběžné uložení pružiny a optimální zavedení síly.

Překročí, když je pružina zatížena Smykové napětí přípustná hodnota nastává trvalá deformace, která se projeví zmenšením nenapnuté délky. V jarní technologii se tento proces nazývá „nastavení“, což je spojeno s pojmy „plíživý“ a „ Relaxace „Z materiálového inženýrství je třeba rovnat.“ Aby se tomu zabránilo, jsou tlačné pružiny navinuty déle o předpokládané množství tuhnutí a později stlačeny na délku bloku. Tato záloha umožňuje lepší využití materiálu a umožňuje vyšší zatížení při pozdějším použití.

 

Výpočtové vzorce válcová tlačná pružina

Výpočet Kompresní pružina na základě výpočtových rovnic podle DIN EN 13906-1:

Technická ilustrace tlačné pružiny

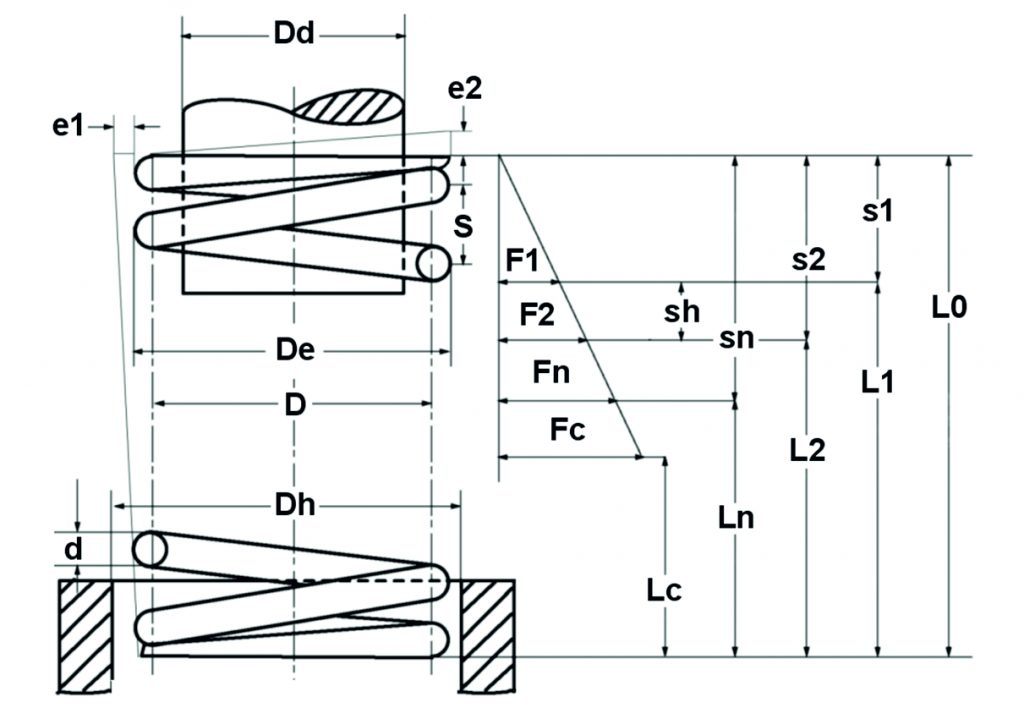
Obrázek: Teoretický diagram tlačné pružiny

 

Důkaz funkce tlačných pružin

Pro válcové tlačné pružiny z drátu kruhového průřezu platí toto:

Jarní sazba: R = \ frac {Gd ^{4} } {8D ^{3} n}

z R = F / s vyplývá:

Síla pružiny: F = \ frac {Gd ^{4} s} {8D ^{3} n}

jako:

Pojezdová dráha: s = \ frac {8D ^{3} nF} {Gd ^{4} }

 

Důkaz pevnosti tlačné pružiny

Po určení rozměrů pružiny musí být pevnost ověřena. K tomu se určí existující smykové napětí:

Napětí z napájení: \tau=\frac<wpml_curved wpml_value='8DF'></wpml_curved>{\pi d^<wpml_curved wpml_value='3'></wpml_curved>}

Napětí z cesty: \ tau = \ frac{Gds} {\ pi n D ^{2} }

Zatímco smykové napětí τ se má použít pro návrh staticky nebo kvazistaticky zatížených pružin, platí následující opravené smykové napětí τ k pro dynamicky namáhané pružiny. Rozložení smykového napětí v průřezu drátu pružiny je nerovnoměrné, nejvyšší napětí nastává na vnitřním průměru pružiny. S korekčním faktorem napětí k, který závisí na poměru navíjení (poměr středního průměru k tloušťce drátu) pružiny, lze přibližně určit nejvyšší napětí. Pro dynamicky namáhané tlačné pružiny výsledek je:

Opravené smykové napětí: \rosa_{k} = k \ tau

kde platí pro k (podle Bergsträssera):

k=\frac{\frac<wpml_curved wpml_value='D'></wpml_curved><wpml_curved wpml_value='d'></wpml_curved>+0,5}{\frac<wpml_curved wpml_value='D'></wpml_curved><wpml_curved wpml_value='d'></wpml_curved>-0,75}

Nyní je provedeno srovnání s povoleným napětím. To je definováno takto:

Přípustné napětí:

\rosa_{ } = 0,5 \ cdot R_ { }

a

\rosa_{ } = 0,56 \ cdot R_ { }

Hodnoty pro Minimální pevnost v tahu R m jsou závislé na tloušťce drátu a lze je najít v normách příslušných materiálů.

Zpravidla musí být možné stlačit tlačné pružiny až do délky bloku, proto je přípustné napětí při délce bloku t czul zvážit.

V případě dynamického zatížení Nízké a vysoké napětí (t k 1 a t k 2) příslušného zdvihu lze určit. Rozdíl je v zdvihovém napětí. Horní napětí i napětí zdvihu nesmí překročit odpovídající přípustné hodnoty. Ty lze najít v diagramech únavové pevnosti v EN 13906-1: 2002. Pokud napětí vydrží toto srovnání, je pružina odolná proti únavě s cyklem mezního zatížení 10 7. .

Geometrické vztahy v tlačných pružinách

Velikost pružiny Výpočtová rovnice
Celkový počet tahů n t = n + 2
Délka bloku zemní pružiny L. C = n t d Max
Délka bloku neleštěného hrotu L. C = (n t + 1,5) d Max
Nejmenší použitelná délka L. n = L C + S. A
Nevázaná délka L. 0 = L n + s n
 

Součet minimálních vzdáleností mezi zatáčkami

 S_{a} = \ vlevo (0,0015 \ frac {D ^{2} }{d} + 0,1d \ vpravo) \ cdot n
Zvětšení vnějšího průměru při zatížení

 

hřiště

  

\ trojúhelník D_{e} = 0,1 \ frac {S ^{2} -08Sd-0,2d ^{2} }{D}

 

S = \ frac{L0-d}{n} (přízemní)

S = \ frac {L0-2,5d}{n} (neleštěný)

 
 

Zdvih vzpěru (platí pro různé Podpůrné koeficienty n, viz EN 13906-1: 2002)

 Vzpěrný zdvih pružiny s formulací kompresní pružiny

 

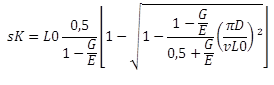Všechny dynamicky namáhané pružiny s jednou velikostí drátu> 1 mm by měl výstřel zaslechl vůle. To zvyšuje únavovou pevnost. Po provedení funkčního ověření a ověření pevnosti je třeba provést a zohlednit různé geometrické výpočty, aby bylo zajištěno, že Kování na peří aby bylo možné vložit do konstrukce součásti. Délka bloku umět nesmí být podříznuto, protože zatáčky jsou těsně proti sobě, což je nejmenší použitelná délka by měl nesmí být podříznut, protože a křivka lineární síly stejně jako dynamická odolnost již nejsou zaručeny. Kromě toho je třeba zohlednit přípustné tolerance podle DIN 2095.

Výpočet tažných pružin

Všeobecné

Tažné pružiny jsou navinuty kolem trnu stejně jako tlačné pružiny, ale bez vzdálenosti mezi vinutími a s různými Tvar očka / Konce pružiny pro připevnění pružiny. Otáčky jsou z hlediska technologie výroby pevně přitlačeny proti sobě. Tento vnitřní Předpětí F 0 závisí na poměru navíjení a nelze jej vyrobit do požadované výšky. Poskytuje referenční hodnoty pro množství předpětí Výpočetní software WinFSB z Gutekunst peří po zadání příslušných údajů o pružině.

Prodlužovací pružiny tvary oček | Gutekunst peří

 

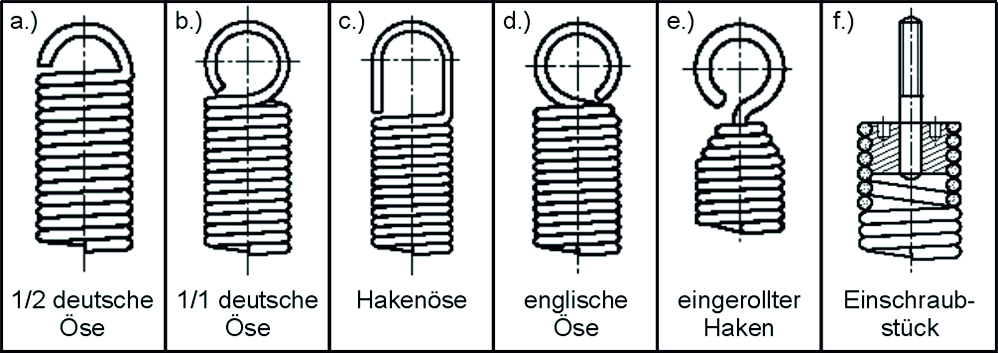
Obrázek: Běžné tvary očka: a.) napůl německé oko; b.) celá německá smyčka; c.) háček oko; d.) anglické očko; e.) zvlněný háček; f.) šroubovací kus

Výhodou tažných pružin je to Svoboda od zalomení Nevýhodou je větší instalační prostor a úplné přerušení toku síly při prasknutí pružiny.

Výpočtové vzorce válcová tažná pružina

Podle výpočtových rovnic pro tlačné pružiny, ale s přihlédnutím k předpínací síle, platí pro válcové tažné pružiny vyrobené z kulatého drátu následující vztahy (viz také obrázek 1.8):

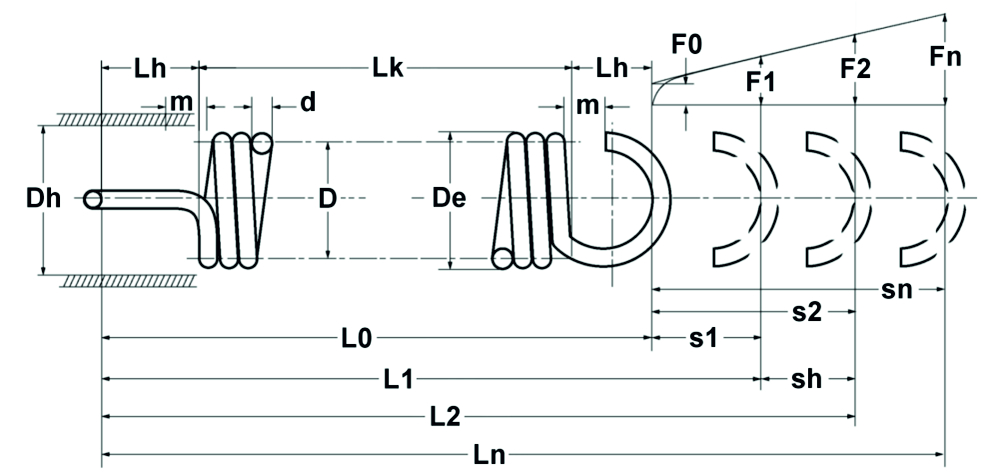
Teoretický diagram tažné pružiny | Gutekunst peří

Obrázek: Teoretický diagram napínací pružiny

 

Důkaz funkce napínací pružiny

Pro válcové tažné pružiny z drátu kruhového průřezu platí:

Jarní sazba: R = \ frac {Gd ^ 4} {8D ^ 3n} = \ frac{F-F0}{s}

z R = F / s vyplývá:

Síla pružiny: F = \ frac {Gd ^ 4s} {8D ^ 3n} + F0

jako:

Pojezdová dráha: s = \ frac {8D ^ 3n (F-F0)} {Gd ^ 4}

 

Důkaz pevnosti tažných pružin

Stejně jako u výpočtů tlačné pružiny je třeba určit stávající smykové napětí.

Smykové napětí: \ tau = \ frac{8DF} {\ pi d ^ 3}

Opravené napětí zdvihu je třeba vypočítat také pro dynamická zatížení.

Opravené smykové napětí: \rosa_{{k} } = k \ tau

Přípustné napětí: \rosa_{ } = 0,45 \ cdot R_ { }

Stávající maximální napětí t n pro největší cestování s n je nastavena na hodnotu rovnající se povolenému napětí. K tomu Relaxace Aby se tomu zabránilo, mělo by se v praxi použít pouze 80% tohoto pojezdu pružiny.

s_ { } = 0,8 \ cdot s_ { }

Pro dynamická zatížení není obecně použitelné Hodnoty únavové pevnosti musí být specifikováno jako Ohybové body očka dochází k dalším napětím, z nichž některá mohou překročit povolená napětí. Tažné pružiny by proto měly být pokud možno vystaveny statickému zatížení. Pokud nelze zabránit dynamickému namáhání, mělo by to být Odstraňte ohnutá očka a válcované nebo zašroubované koncové kusy vložte e. Zkouška životnosti za pozdějších provozních podmínek má smysl. Zpevnění povrchu Kuličkování není možné z důvodu těsných zatáček.

 

Geometrické vztahy v tažných pružinách

Velikost pružiny Výpočtová rovnice
délka těla L. K. = (n t + 1) d
Nevázaná délka L. 0 = L K. + 2 l H
Výška očí polovina německého oka L. H = 0,55 D. i až 0,80 D. i
Výška očí celé německé oko L. H = 0,80 D. i do 1.10D i
Výška háku oka L. H> 1. 10D i
Výška očka Anglické očko L. H = 1,10D i

Je třeba zohlednit povolené výrobní tolerance podle DIN 2097.

 

Výpočet torzních pružin (torzní pružiny)

Všeobecné

Spirálová válcová Pružiny nohou (Torzní pružiny) mají v podstatě stejný tvar jako válcové tlak – a Tažné pružiny , ale s výjimkou konce pružiny. Ty jsou ohnuty ve tvaru nohy, aby se umožnilo tělu pružiny otáčet se kolem osy pružiny. To znamená, že existuje velmi mnoho různých oblastí použití, například jako vratné nebo závěsné pružiny. Zkrutná pružina by měla být namontována na vodicí trn a zatížení by mělo působit pouze ve směru navíjení. Zde je zmenšen vnitřní průměr. Pružiny jsou obvykle stočeny bez rozteče. Pokud je však tření absolutně nežádoucí, lze torzní pružiny vyrobit také s roztečí cívky. V případě dynamického zatížení je třeba zajistit, aby na koncích pružiny nebyly žádné ostré ohyby, aby se zabránilo nepředvídatelným špičkám napětí.

Výpočtové vzorce pro válcové torzní pružiny (Torzní pružiny)

Výpočet je založen na pokynech EN 13906-3: 2001:

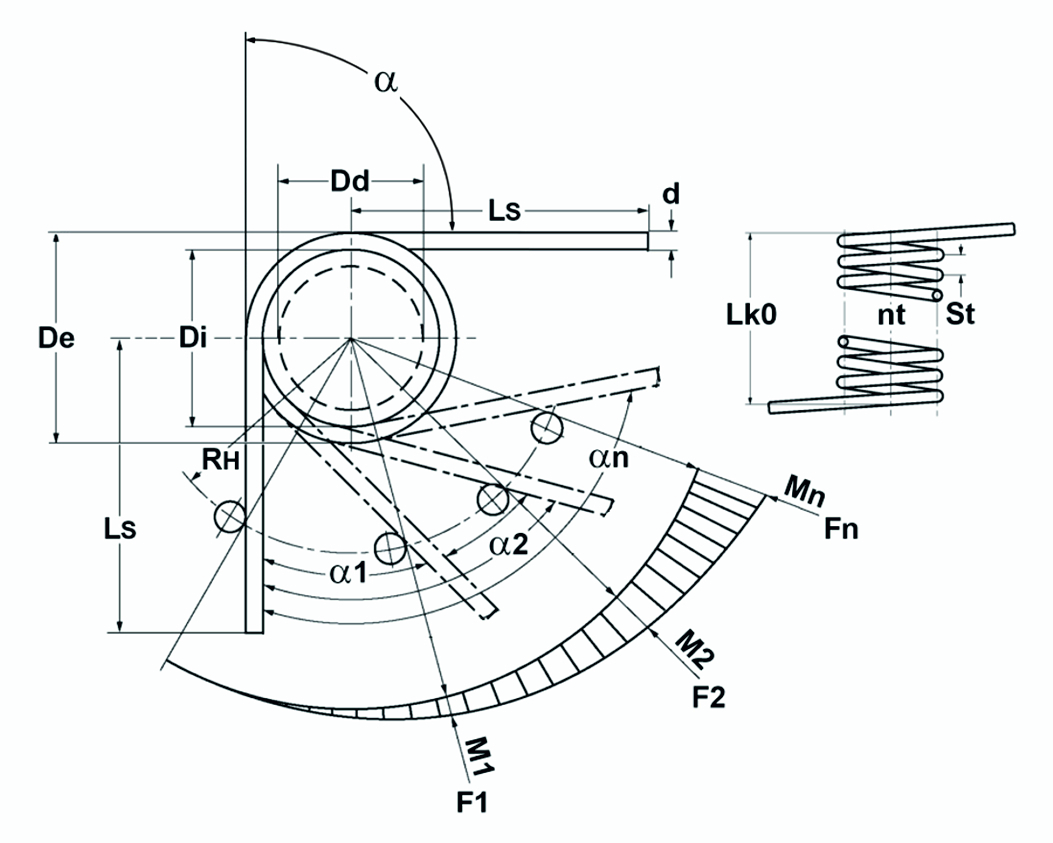
Teoretický diagram pružin nohy | Gutekunst peří

Obrázek: Teoretický diagram torzní pružiny / torzní pružiny

Důkaz funkce torzních pružin (torzní pružiny)

Rychlost točivého momentu pružiny: R_{M} = \ frac{M} {\ alpha} = \ frac {d ^ 4E}{3667Dn}

 

Krouticí moment pružiny: M = FR_{H} = \ frac {d ^ 4E \ alpha}{3667Dn}

 

Úhel natočení: \ alfa = \ frac{3667DMn} {Ed ^ 4}

 

Důkaz pevnosti torzních pružin (torzní pružiny)

Stávající ohybové napětí se stanoví a porovná s přípustným napětím. V případě dynamického zatížení je nutné pro srovnání znovu použít opravené napětí.

Napětí v ohybu: \ sigma = \ frac{32M} {\ pi d ^ 3}

Opravené napětí v ohybu: \ sigma_ {{q} } = q \ sigma

kde platí q:

q = \ frac {\ frac{D}{d} +0,07} {\ frac{D}{d} -0,75}

 

Přípustné napětí v ohybu: \ sigma_ {{zul} } = 0,7 Rm

 

V případě dynamického zatížení je spodní a horní napětí (t k 1 a t k 2) příslušného zdvihu lze určit. Rozdíl je v zdvihovém napětí. Horní napětí i napětí zdvihu nesmí překročit odpovídající přípustné hodnoty. U drátů z pružinové oceli je lze najít v diagramech únavové pevnosti v EN 13906-3: 2001. Pokud napětí vydrží toto srovnání, je pružina odolná proti únavě s cyklem mezního zatížení 10 7. .

 

Geometrické vztahy v torzních pružinách (torzní pružiny)

Velikost pružiny Výpočtová rovnice
 

Zmenšení vnitřního průměru při maximálním zatížení

 Di_{n} = \ frac{Dn} {n + \ frac {\ alpha}{360} } -d
Nezatížená délka těla Lk = (n + 1,5) d
Délka těla v maximálně zatíženém stavu Lk_{n} = (n + 1,5 + \ frac {\ alfa}{360} ) d
Pojezdová dráha s_{n} = \ frac {\ alfa_{n} R_{H} } {57,3}

Kromě toho je třeba zohlednit výrobní tolerance podle DIN 2194.

 

Shrnutí článku „Návrh kovové pružiny“, který se skládá z Část 1 „Základy“ a část 2 „Výpočet“ lze také stáhnout z webu Gutekunst pružiny 1×1 .

Pokud byste ho potřebovali individuální design pružiny pošlete nám e-mailem klíčová data pro kovovou pružinu, kterou potřebujete technik@gutekunst-co.com , kontaktujte naše technologické oddělení telefonicky na (+49) 035 877 227-11 nebo použijte na https://www.federnshop.com the Program výpočtu pružin Gutekunst WinFSB pro bezplatný výpočet tlačných pružin, tažných pružin a torzních pružin.

Dodatečné informace:

 

Návrh kovových pružin – Část 2 „Výpočet“
Štítky: