Níže je uveden souhrn základních informací o Jarní design z Tlačné pružiny , Tažné pružiny a Pružiny nohou .
Technické pružiny jsou dodnes jedním z nejdůležitějších prvků stroje a úspěšně se používají ve vozidlech, přesných mechanických nebo elektrotechnických zařízeních, zdravotnických zařízeních, domácích spotřebičích a mnoha dalších. Funkce celého zařízení nebo části stroje často závisí na bezproblémovém provozu kovové pružiny.
Kovové pružiny jsou prvky, které se při zatížení záměrně deformují a po odstranění zatížení se vrátí do původního tvaru. Dodaná energie je uvnitř Jarní práce (W) přeměněn a znovu uvolněn v pozdějším okamžiku (zásobník energie). Kovové pružiny však spolehlivě provádějí tuto deformaci a absorpci energie pouze v mezích určených pro tento účel. Proto je ten pravý Jarní design a Výpočet pružiny důležitý komponent pro perfektně fungující kovovou pružinu.
Table of Contents
Charakteristická křivka pružiny
Kovové pružiny nebo technické pružiny jsou vyráběny podle vašich Jarní charakteristika soudě. Tato charakteristika pružiny představuje závislost Síla pružiny (F) představuje zdvih pružiny. Protože v závislosti na tom, která charakteristika pružiny je požadována (lineární, progresivní, degresivní nebo kombinovaná), se mění také tvar a typ pružiny.
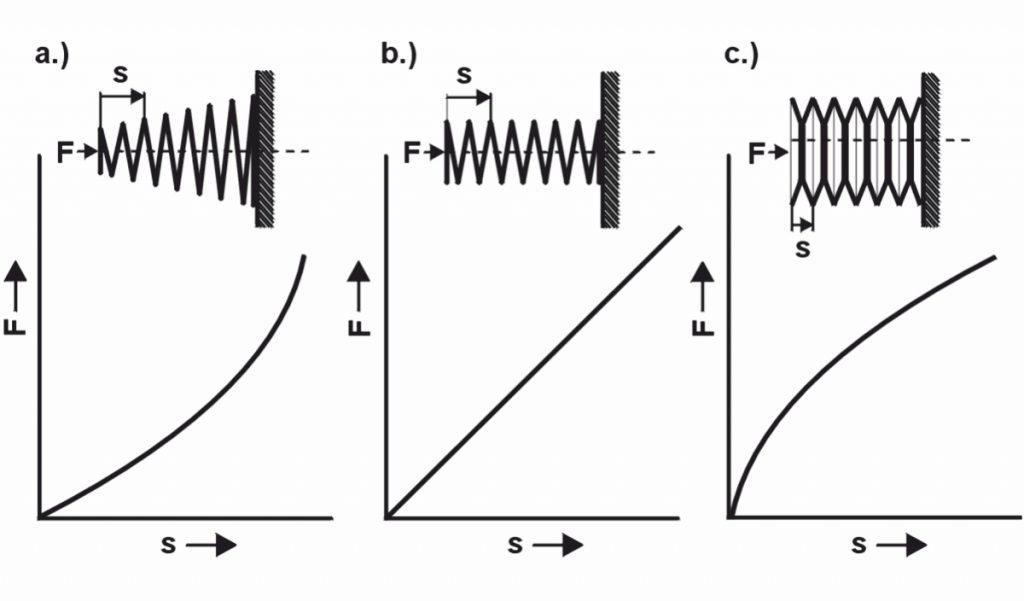
S Jarní sazba (R) charakteristika pružiny je určena v diagramu pružiny. Míra pružiny (R) je proto důležitou hodnotou při návrhu pružiny pro správnou pružinu. V lineární charakteristika pružiny pružina je konstantní. Pružiny se zakřivenou charakteristikou pružiny mají proměnnou rychlost pružení. Následující vzorce tedy platí pro lineární charakteristiku:
pro tlačné a tažné pružiny
R=\frac{F2-F1}{s2-s1}pro nohy a torzní pružiny
R_{M}=\frac{M2-M1}{\alpha2-\alpha1}
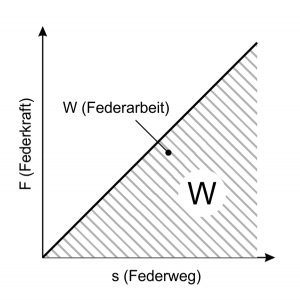
Jarní práce
Když je kovová pružina napnutá, je práce hotová, která se poté po uvolnění napětí znovu uvolní. Pružinová práce (W) je vždy výsledkem oblasti pod charakteristikou pružiny. U lineární charakteristiky pružiny platí:
pro tlačné a tažné pružiny
W=\frac{1}{2}F\cdot spro nohy a torzní pružiny
W=\frac{1}{2}M\cdot \alphaVýpočtem objemové užitné hodnoty lze určit různé typy pružin pomocí poměru pružinových prací (W) a instalační prostor (V) vzájemné srovnání:
\eta_{A}=\frac{W}{V}
Hystereze
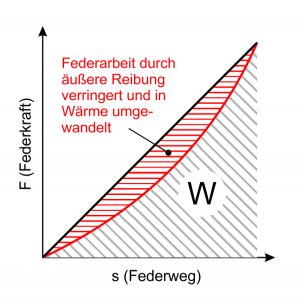
Chování odpružení může být ovlivněno vnějším třením. Tyto třecí síly brání zotavení pružiny. V případě střídavého zatížení je to vyjádřeno formou a Hysterezní smyčka . Část pružinových prací se třením přemění na teplo a poté se „ztratí“. Protože je to při použití pružin nežádoucí, jakékoli tření by mělo být navrženo uspořádáním a Tvar peří je třeba se vyhnout.
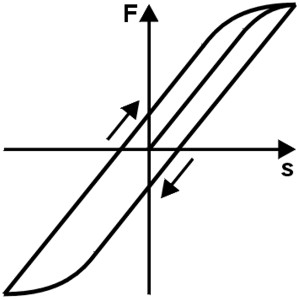
Relaxace
Například pokud je použita tlačná pružina vyšší teplota je stlačen na určitou délku mezi rovnoběžnými deskami, lze určit, že Síla pružiny postupně klesá. Tato ztráta síly se zvyšuje se zvyšující se teplotou a napětím.
Relaxace materiálu je plastická deformace, která se projevuje ztrátou síly při konstantní délce instalace. Udává se jako procento výstupní síly F1:
Relaxace=\frac{\Delta F\cdot 100}{F1}Následující diagram ukazuje základní průběh relaxace a rychlost relaxace:
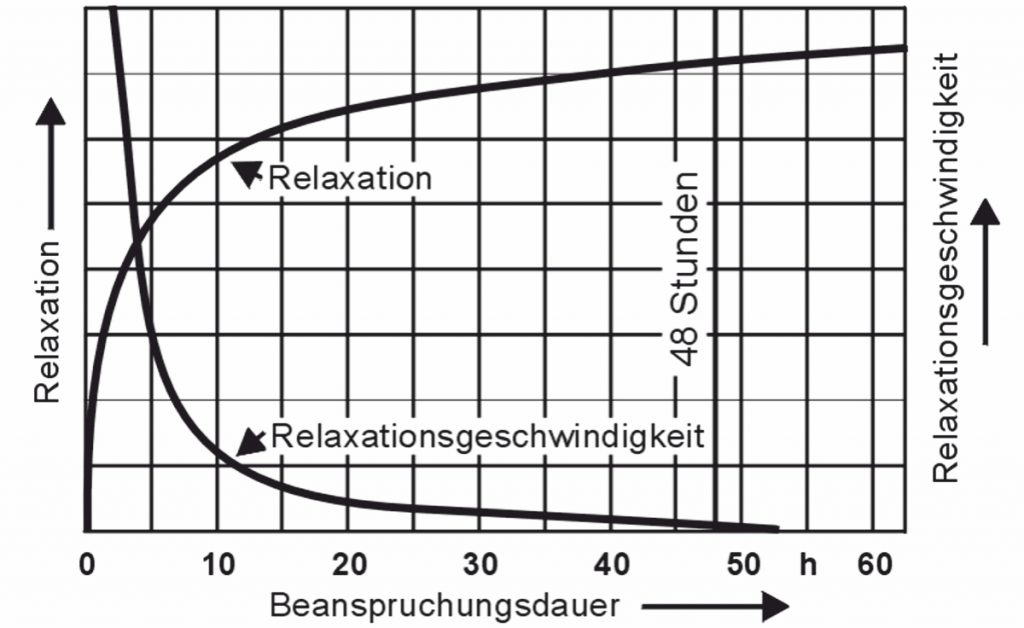
Hodnoty relaxace po 48 hodinách se považují za charakteristické hodnoty, i když relaxace v tomto okamžiku ještě není úplně úplná. Materiálově závislé relaxační diagramy najdete v EN 13906-1. Ty musí projektant zahrnout, pouze pokud jsou kladeny vysoké nároky na stálost síly pružiny. Relaxace při různých teplotních stavech se používá při výpočtu v Jarní výpočetní program WinFSB od Gutekunst Federn, k dispozici na www.federnshop.com , zobrazeno s.
Správná volba materiálu pružiny
Kovové pružiny musí být vyrobeny z vhodného materiálu a musí být navrženy a tvarovány tak, aby se po odstranění působícího zatížení vrátily do původního tvaru. Tato vlastnost je vyjádřena v modul pružnosti a v posuvném modulu. Tyto Parametry materiálu vyjádřit vztah mezi napětím a prodloužením a měl by mít co nejvyšší hodnotu.
Pružinové materiály by navíc měly:
- vysoké limity pružnosti, tj. velký, čistě elastický rozsah,
- odpovídající napětí také na zvýšené teploty vydržet bez větší ztráty síly (nízká relaxace),
- mají vysokou únavovou pevnost (jemnozrnná struktura, bez nečistot),
- mít dostatečnou deformovatelnost,
- mít povrch, který je co nejvíce kluzký,
- odolávat určitým požadavkům na ochranu proti korozi,
- být elektricky vodivé nebo nemagnetické.
Pružnost a moduly kluzu různých pružinových materiálů
| Federwerkstoff | Modul pružnosti [N/mm²] | G modul [N/mm²] |
| Patentovaný tažený drát z pružinové oceli podle EN 10270-1 | 206000 | 81500 |
| Olejem temperovaný drát pružiny ventilu podle EN 10270-2 | 206000 | 81500 |
| Ocel válcovaná za tepla podle EN10089 | 206000 | 78500 |
| Pás válcovaný za studena podle EN 10132 | 206000 | 78500 |
| X10 CrNi 18 8 (1.4310) | 185000 | 70000 |
| X7 CrNiAl 17 7 (1,4568) | 195000 | 73000 |
| X5 CrNiMo 17-12-2 (1.4401) | 180000 | 68000 |
| CuSn6 R950 podle EN 12166 | 115000 | 42000 |
| CuZn36 R700 podle EN 12166 | 110000 | 39000 |
| CuBe2 podle EN 12166 | 120000 | 47000 |
| CuNi18Zn20 podle EN 12166 | 135000 | 45000 |
| CuCo2Be podle EN 12166 | 130000 | 48000 |
| Inconel X750 | 213000 | 76000 |
| Nimonic 90 | 213000 | 83000 |
| Hastelloy C4 | 210000 | 76000 |
| Titanová slitina TiAl6V4 | 104000 | 39000 |
Vliv pracovní teploty na výběr materiálu pružiny
Chování při zvýšených pracovních teplotách
Úroveň pracovní teploty může významně ovlivnit funkci pružiny, protože se zvyšující se teplotou stoupá tendence k relaxaci. Po vyhodnocení relaxačních diagramů lze pro nejdůležitější materiály pružiny nastavit následující mezní teploty.
Omezte teploty pružinových materiálů s minimální relaxací
| Federwerkstoff | Maximální pracovní teplota ve ° C při | |
| vysoké zatížení | nízké zatížení | |
| Patentovaný tažený drát z pružinové oceli podle EN 10270-1 | 60-80 | 80-150 |
| Olejem temperovaný drát pružiny ventilu podle EN 10270-2 | 80-160 | 120-160 |
| X10CrNi 18,8 (1,4310) | 160 | 250 |
| X7CrNiAl 17,7 (1,4568) | 200 | 350 |
| X5CrNiMo 17-12-2 (1.4401) | 160 | 300 |
| CuSn6 | 80 | 100 |
| CuZn36 | 40 | 60 |
| CuBe2 | 80 | 120 |
| CuNi18Zn20 | 80 | 120 |
| Inconel X750 | 475 | 550 |
| Nimonic90 | 500 | 500 |
Kromě toho vezměte důležité pro funkci pružiny Vlastnosti materiálu modul pružnosti a modul smyku klesá s rostoucí teplotou. Jak modul smyku, tak modul pružnosti se stanoví při vyšší teplotě pomocí následujícího vzorce, přičemž základem jsou materiálové parametry při teplotě místnosti (20 ° C).
G_{t}=G_{20}=\frac{3620-T}{3600}nebo.
E_{t}=E_{20}=\frac{3620-T}{3600}
To umožňuje projektantovi určit skutečné síly pružiny při očekávané provozní teplotě.
Chování při nízkých provozních teplotách
Při použití v chladicích systémech ve vesmíru nebo když je v zimě velmi chladno, je nutné vydržet teploty až – 200 °. Přes stoupání pevnost v tahu nízké teploty mají nepříznivý účinek, protože se snižuje houževnatost materiálů a mohou nastat křehké lomy. Nerezové pružinové oceli, jakož i slitiny mědi a niklu jsou výhodnější než patentované pružinové dráty a dráty ventilových pružin, pokud se používají při nízkých teplotách. V následující tabulce jsou uvedeny mezní teploty.
Doporučení pro použití při nízkých teplotách
| Federwerkstoff | Minimální pracovní teplota ve ° C |
| Patentovaný tažený drát z pružinové oceli podle EN 10270-1 | -60 |
| Olejem temperovaný drát pružiny ventilu podle EN 10270-2 | -60 |
| X10CrNi 18,8 (1,4310) | -200 |
| X7CrNiAl 17,7 (1,4568) | -200 |
| X5CrNiMo 17-12-2 (1.4401) | -200 |
| CuSn6 | -200 |
| CuZn36 | -200 |
| CuBe2 | -200 |
| CuNi18Zn20 | -200 |
| Inconel X750 | -100 |
| Nimonic90 | -100 |
Použití pružinových systémů
Z konstrukčních důvodů je také možné použít několik pružin k absorbování sil a pohybů. Jednoduchý Pružinové systémy jsou Paralelní – a Sériová připojení .
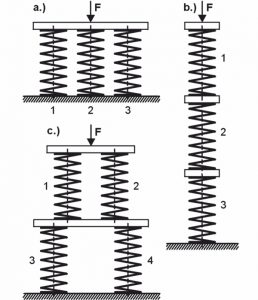
A) Paralelní připojení
Pružiny jsou uspořádány tak, že vnější zatížení (F) je proporcionálně rozděleno mezi jednotlivé pružiny, ale pohyb jednotlivých pružin je stejný. Výsledkem je:
s=s1=s2=s3=... (celkový zdvih zavěšení) F=F1+F2+F3+... (celková síla pružiny) R=R1+R2+R3+... (celková pružnost)Pružnost celkového systému paralelního spojení je vždy větší než pružina jednotlivých pružin
b) Sériové připojení
Pružiny jsou uspořádány jeden za druhým, takže na každou pružinu působí stejná síla, ale dráha pružiny je rozdělena mezi jednotlivé pružiny. Výsledkem je:
s=s1+s2+s3+... (celková dráha zavěšení) F=F1=F2=F3=... (celková síla pružiny) R=\frac{1}{\frac{1}{R1}+\frac{1}{R2}+\frac{1}{R3}+...} (Celková rychlost pružiny)Pružina celkového systému sériového připojení je vždy menší než pružina jednotlivých pružin
C) Smíšený obvod
Několik pružin je spojeno paralelně a jeden za druhým. Kvůli rovnováze musí být R1 = R2 a R3 = R4. V uvedeném případě platí následující:
R=\frac{1}{\frac{1}{R1+R2}+\frac{1}{R3+R4}+...} (Celková rychlost pružiny)Pružina zobrazeného celého systému směšovacího okruhu leží mezi nejmenší a největší pružinou jednotlivých pružin!
Ve druhé části informační série Návrh kovových pružin – část 2 „Výpočet „poskytujeme vám parametry výpočtu pro Ověření funkce a pevnosti the Tlačné pružiny , Tažné pružiny a Pružiny nohou vpředu.
Pokud potřebujete návrh pružiny na míru, stačí nám zaslat klíčové údaje o požadované kovové pružině na adresu service@federnshop.com, kontaktovat naše technické oddělení na telefonním čísle (+49) 035877 227-11 nebo použít program pro výpočet pružin WinFSB společnosti Gutekunst na adrese www.federnshop.com, kde je výpočet tlačných, tažných a torzních pružin zdarma.
Dodatečné informace: