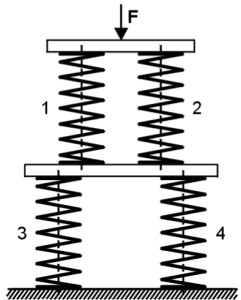
To absorb forces and movements are sometimes also Spring systems used. Due to the different arrangement of Compression springs A wide variety of force properties can be generated.
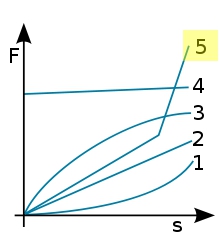
Simple spring systems are:
Table of Contents
Compression springs parallel connection
The springs are arranged in such a way that the external load “F” is proportionally divided between the individual springs, but the travel of the individual springs is the same. So it results:
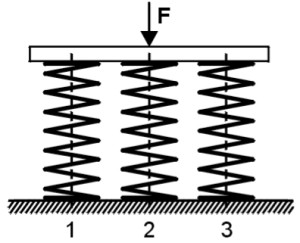
Total suspension travel: s = s1 = s2 = s3
Total spring force: F = F1 + F2 + F3
Total spring rate: R = R1 + R2 + R3
annotation : The Spring rate of the overall system of a Parallel connection is always greater than that Spring rate of the individual springs.
Compression springs connected in series
The springs are arranged one behind the other so that the same force acts on each spring, but the spring travel is divided between the individual springs. So it results:
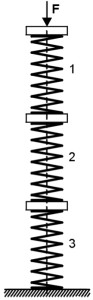
Total suspension travel: s = s1 + s2 + s3 + …
Total spring force: F = F1 = F2 = F3 = …
Total spring rate:
annotation : The spring rate of the overall system of a Series connection is always smaller than that Spring rate of the individual springs.
Compression springs Mixed circuits of individual springs
In the Mixed circuit several springs are connected in parallel and one behind the other. The following formula results for the total spring rate: