Poniżej znajduje się podsumowanie podstaw dotyczących Wiosenny projekt z Sprężyny dociskowe , Sprężyny naciągowe i Sprężyny nóg .
Sprężyny techniczne są dziś nadal jednym z najważniejszych elementów maszyn i są z powodzeniem stosowane w pojazdach, precyzyjnych urządzeniach mechanicznych czy elektrotechnicznych, urządzeniach medycznych, sprzęcie AGD i wielu innych. Działanie całego urządzenia lub części maszyny zależy często od bezawaryjnej pracy metalowej sprężyny.
Sprężyny metalowe to elementy, które celowo odkształcają się pod obciążeniem i wracają do swojego pierwotnego kształtu po zdjęciu obciążenia. Dostarczona energia jest w Wiosenna praca (W) przekształca się i ponownie uwalnia w późniejszym czasie (magazyn energii). Jednak metalowe sprężyny niezawodnie wykonują to odkształcenie i pochłanianie energii tylko w granicach przewidzianych do tego celu. Dlatego jest właściwy Wiosenny projekt i Obliczenia sprężyny ważny składnik doskonale działającej metalowej sprężyny.
Table of Contents
Krzywa charakterystyki sprężyny
Sprężyny metalowe lub techniczne wykonujemy według Państwa Charakterystyka wiosny oceniał. Ta charakterystyka sprężyny reprezentuje zależność Siła sprężyny (F) przedstawia skok (y) sprężyny. Ponieważ w zależności od tego, która charakterystyka sprężyny jest wymagana (liniowa, progresywna, degresywna lub kombinowana), zmienia się również kształt i typ sprężyny.
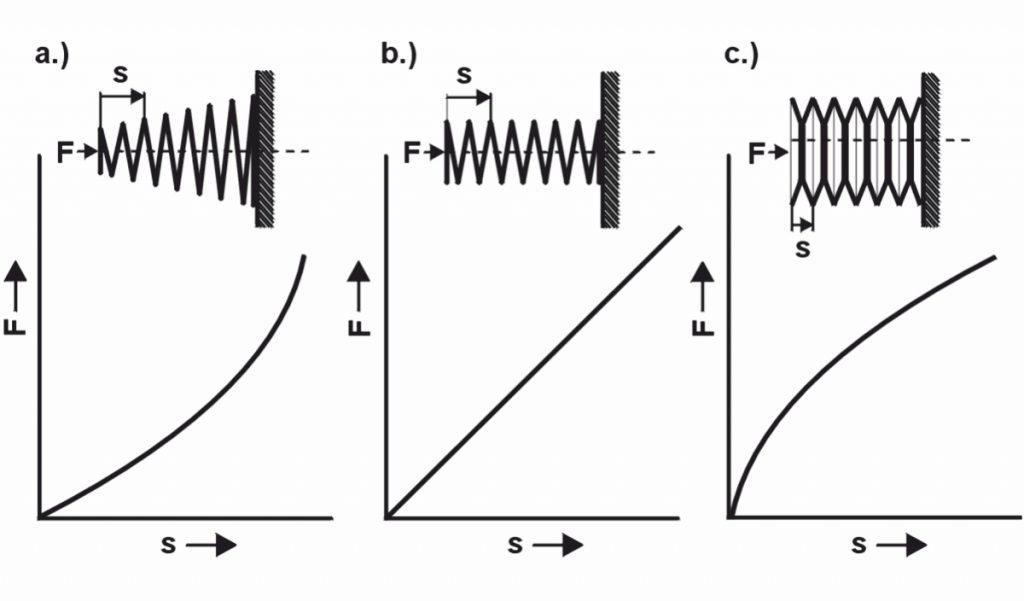
Dzięki Wiosenna stawka (R) charakterystyka sprężyny jest określona na schemacie sprężyny. Współczynnik sztywności (R) jest zatem ważną wartością przy projektowaniu sprężyny dla właściwej sprężyny. W liniowa charakterystyka sprężyny sztywność sprężyny jest stała. Sprężyny o zakrzywionej charakterystyce sprężyny mają zmienną sztywność. Dlatego do charakterystyki liniowej mają zastosowanie następujące wzory:
do sprężyn naciskowych i naciągowych
R=\frac{F2-F1}{s2-s1}do nóg i sprężyn skrętnych
R_{M}=\frac{M2-M1}{\alpha2-\alpha1}
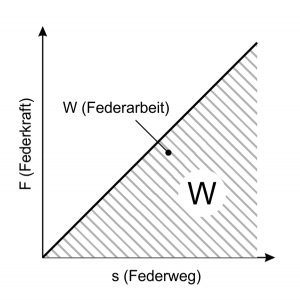
Wiosenna praca
Gdy metalowa sprężyna jest naprężona, praca jest wykonywana, która jest następnie ponownie zwalniana po zwolnieniu naciągu. Praca sprężyny (W) zawsze jest obszarem poniżej charakterystyki sprężyny. W przypadku liniowej charakterystyki sprężyny obowiązuje:
do sprężyn naciskowych i naciągowych
W=\frac{1}{2}F\cdot sdo nóg i sprężyn skrętnych
W=\frac{1}{2}M\cdot \alphaObliczając wartość użytkową objętości, można określić różne typy sprężyn na podstawie współczynnika pracy sprężyny (W) i przestrzeń montażową (V) porównaj ze sobą:
\eta_{A}=\frac{W}{V}
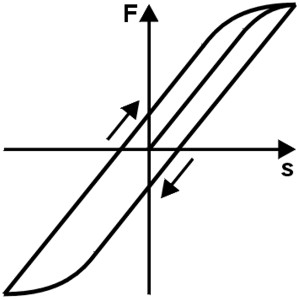
Histereza
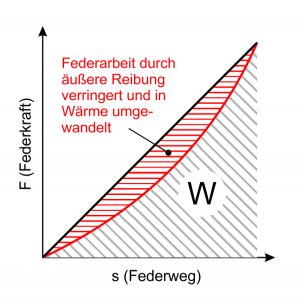
Na zachowanie zawieszenia może wpływać tarcie zewnętrzne. Te siły tarcia utrudniają powrót sprężyny. W przypadku obciążeń przemiennych jest to wyrażone w postaci a Pętla histerezy . Część pracy sprężyny jest zamieniana na ciepło w wyniku tarcia, a następnie „tracona”. Ponieważ jest to niepożądane w przypadku stosowania sprężyn, wszelkie tarcie należy zaplanować zgodnie z układem i Kształt piór być unikanym.
Relaks
Na przykład, jeśli używana jest sprężyna naciskowa podwyższona temperatura jest ściskany do określonej długości między równoległymi płytami, można stwierdzić, że Siła sprężyny stopniowo maleje z czasem. Ta utrata siły wzrasta wraz ze wzrostem temperatury i napięcia.
Relaks materiału to odkształcenie plastyczne, które objawia się utratą siły przy stałej długości montażowej. Jest to wyrażone jako procent siły wyjściowej F1:
Relaksacja=\frac{\Delta F\cdot 100}{F1}Poniższy diagram przedstawia podstawowy przebieg relaksacji i prędkość relaksacji:
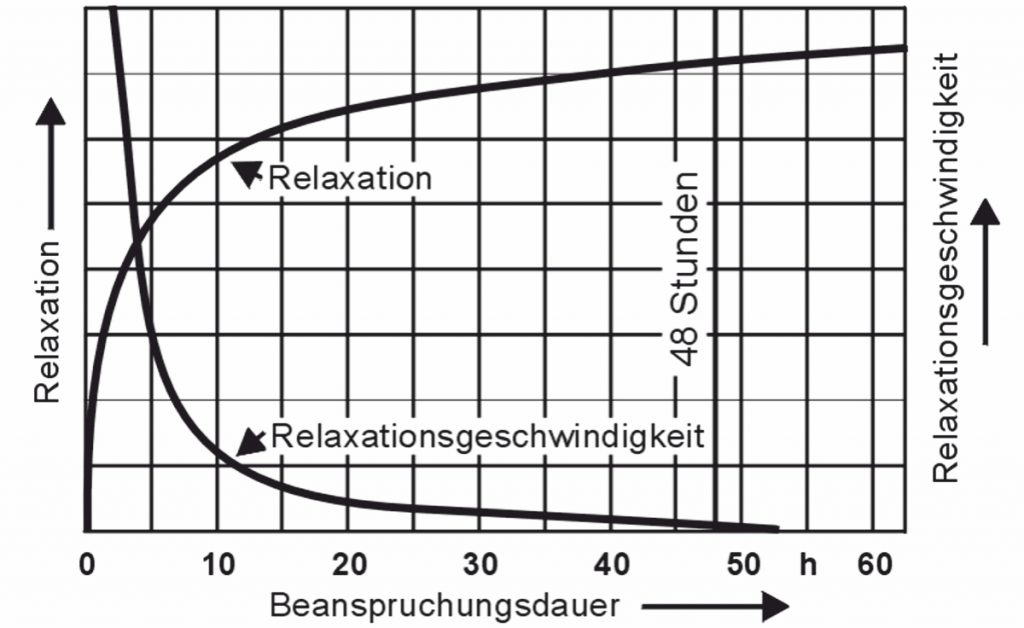
Wartości relaksacji po 48 godzinach uważa się za wartości charakterystyczne, chociaż relaksacja nie jest jeszcze w tym momencie całkowicie zakończona. Diagramy relaksacji zależnej od materiału można znaleźć w normie EN 13906-1. Projektant powinien je uwzględnić tylko wtedy, gdy stawiane są wysokie wymagania co do stałości siły sprężyny. W obliczeniach wykorzystuje się relaksację w różnych stanach temperaturowych Program do obliczania sprężyn WinFSB firmy Gutekunst Federn, dostępny pod adresem www.federnshop.com , pokazane z.
Właściwy wybór materiału sprężyny
Sprężyny metalowe muszą być wykonane z odpowiedniego materiału sprężynowego oraz zaprojektowane i ukształtowane w taki sposób, aby powracały do swojego pierwotnego kształtu po usunięciu przyłożonego obciążenia. Ta właściwość jest wyrażona w moduł sprężystości oraz w module przesuwnym. Te Parametry materiałowe wyrażają zależność między napięciem a wydłużeniem i powinny mieć możliwie najwyższą wartość.
Ponadto materiały sprężynowe powinny:
- wysokie limity elastyczności, czyli duży, czysto elastyczny zakres,
- odpowiednie napięcia również przy podwyższonych temperaturach wytrzymać bez większej utraty siły (niski relaks),
- mają dużą wytrzymałość zmęczeniową (drobnoziarnista struktura, wolna od zanieczyszczeń),
- mieć wystarczającą odkształcalność,
- mieć możliwie jak najbardziej śliską powierzchnię,
- wytrzymują określone wymagania dotyczące ochrony antykorozyjnej,
- przewodzić prąd elektryczny lub być niemagnetyczny.
Moduły sprężystości i poślizgu różnych materiałów sprężynowych
| Materiał sprężynowy | Moduł sprężystości [N/mm²] | Moduł G. [N/mm²] |
| Opatentowany ciągniony drut ze stali sprężynowej zgodnie z EN 10270-1 | 206000 | 81500 |
| Odpuszczany w oleju drut sprężynowy zaworowy zgodnie z EN 10270-2 | 206000 | 81500 |
| Stal walcowana na gorąco zgodnie z EN10089 | 206000 | 78500 |
| Taśma walcowana na zimno zgodnie z EN 10132 | 206000 | 78500 |
| X10 CrNi 18 8 (1.4310) | 185000 | 70000 |
| X7 CrNiAl 17 7 (1.4568) | 195000 | 73000 |
| X5 CrNiMo 17-12-2 (1.4401) | 180000 | 68000 |
| CuSn6 R950 zgodnie z EN 12166 | 115000 | 42000 |
| CuZn36 R700 zgodnie z EN 12166 | 110000 | 39000 |
| CuBe2 zgodnie z EN 12166 | 120000 | 47000 |
| CuNi18Zn20 zgodnie z EN 12166 | 135000 | 45000 |
| CuCo2Be zgodnie z EN 12166 | 130000 | 48000 |
| Inconel X750 | 213000 | 76000 |
| Nimonic 90 | 213000 | 83000 |
| Hastelloy C4 | 210000 | 76000 |
| Stop tytanu TiAl6V4 | 104000 | 39000 |
Wpływ temperatury roboczej na wybór materiału sprężyny
Zachowanie w podwyższonych temperaturach roboczych
Poziom temperatury pracy może znacząco wpływać na działanie sprężyny, ponieważ wraz ze wzrostem temperatury wzrasta tendencja do relaksacji. Po przeanalizowaniu wykresów relaksacji można ustawić następujące temperatury graniczne dla najważniejszych materiałów sprężystych.
Ogranicz temperatury materiałów sprężystych przy minimalnym relaksacji
| Materiał sprężynowy | Maksymalna temperatura robocza w ° C przy | |
| wysokie obciążenia | niskie obciążenie | |
| Opatentowany ciągniony drut ze stali sprężynowej zgodnie z EN 10270-1 | 60-80 | 80-150 |
| Odpuszczany w oleju drut sprężynowy zaworowy zgodnie z EN 10270-2 | 80-160 | 120-160 |
| X10CrNi 18,8 (1,4310) | 160 | 250 |
| X7CrNiAl 17,7 (1,4568) | 200 | 350 |
| X5CrNiMo 17-12-2 (1.4401) | 160 | 300 |
| CuSn6 | 80 | 100 |
| CuZn36 | 40 | 60 |
| CuBe2 | 80 | 120 |
| CuNi18Zn20 | 80 | 120 |
| Inconel X750 | 475 | 550 |
| Nimonic90 | 500 | 500 |
Ponadto weź to, co ważne dla funkcji sprężyny Właściwości materiału moduł sprężystości a moduł ścinania zmniejsza się wraz ze wzrostem temperatury. Zarówno moduł sprężystości na ścinanie, jak i moduł sprężystości wyznacza się w wyższej temperaturze przy użyciu następującego wzoru, przy czym za podstawę służą parametry materiału w temperaturze pokojowej (20 ° C).
G_{t}=G_{20}=\frac{3620-T}{3600}lub.
E_{t}=E_{20}=\frac{3620-T}{3600}
Umożliwia to projektantowi określenie rzeczywistych sił sprężyn w oczekiwanej temperaturze pracy.
Zachowanie w niskich temperaturach roboczych
W przypadku stosowania w układach chłodzenia w kosmosie lub gdy jest bardzo zimno zimą, należy wytrzymać temperatury sięgające – 200 ° C. Pomimo wzrostu Wytrzymałość na rozciąganie niskie temperatury mają niekorzystny wpływ, ponieważ twardość materiałów spada i mogą wystąpić kruche pęknięcia. Nierdzewne stale sprężynowe, a także stopy miedzi i niklu są preferowane niż opatentowane druty sprężynowe i druty sprężyn zaworowych, gdy są używane w niskich temperaturach. Poniższa tabela przedstawia temperatury graniczne.
Zalecenia dotyczące stosowania w niskich temperaturach
| Materiał sprężynowy | Minimalna temperatura robocza w ° C |
| Opatentowany ciągniony drut ze stali sprężynowej zgodnie z EN 10270-1 | -60 |
| Odpuszczany w oleju drut sprężynowy zaworowy zgodnie z EN 10270-2 | -60 |
| X10CrNi 18,8 (1,4310) | -200 |
| X7CrNiAl 17,7 (1,4568) | -200 |
| X5CrNiMo 17-12-2 (1.4401) | -200 |
| CuSn6 | -200 |
| CuZn36 | -200 |
| CuBe2 | -200 |
| CuNi18Zn20 | -200 |
| Inconel X750 | -100 |
| Nimonic90 | -100 |
Zastosowanie systemów sprężynowych
Ze względów konstrukcyjnych możliwe jest również użycie kilku sprężyn do absorbowania sił i ruchów. Prosty Systemy sprężynowe są Równolegle – i Połączenia szeregowe .
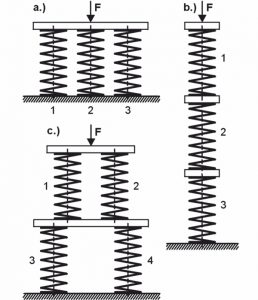
za) Połączenie równoległe
Sprężyny są rozmieszczone w taki sposób, że obciążenie zewnętrzne (F) jest proporcjonalnie podzielone między poszczególne sprężyny, ale droga poszczególnych sprężyn jest taka sama. Wynika z tego:
s=s1=s2=s3=... (całkowity skok zawieszenia) F=F1+F2+F3+... (całkowita siła sprężyny) R=R1+R2+R3+... (całkowity współczynnik sprężystości)Sztywność całego systemu połączenia równoległego jest zawsze większa niż sztywność poszczególnych sprężyn
b) Połączenie szeregowe
Sprężyny są rozmieszczone jedna za drugą, tak że na każdą sprężynę działa ta sama siła, ale skok sprężyny jest podzielony między poszczególne sprężyny. To skutkuje:
s=s1+s2+s3+... (całkowity skok zawieszenia) F=F1=F2=F3=... (całkowita siła sprężyny) R=\frac{1}{\frac{1}{R1}+\frac{1}{R2}+\frac{1}{R3}+...} (Całkowita sprężystość)Sztywność całego systemu połączenia szeregowego jest zawsze mniejsza niż sztywność poszczególnych sprężyn
do) Obieg mieszany
Kilka sprężyn jest połączonych równolegle i jedna za drugą. Ze względu na równowagę, R1 = R2 i R3 = R4 muszą być. W przedstawionym przypadku obowiązują następujące zasady:
R=\frac{1}{\frac{1}{R1+R2}+\frac{1}{R3+R4}+...} (Całkowita sprężystość)Sztywność całego układu pokazanego obwodu mieszającego zawiera się pomiędzy najmniejszą a największą sztywnością poszczególnych sprężyn!
W drugiej części serii informacyjnej „ Projektowanie sprężyn metalowych – Część 2 „Obliczenia „zapewniamy parametry obliczeniowe dla Weryfikacja funkcji i wytrzymałości the Sprężyny dociskowe , Sprężyny naciągowe i Sprężyny nóg z przodu.
Jeśli potrzebujesz niestandardowego projektu sprężyny, po prostu wyślij nam e-mailem kluczowe dane dotyczące metalowej sprężyny, której potrzebujesz, na adres service@federnshop.com, skontaktuj się z naszym działem technicznym telefonicznie pod numerem (+49) 035877 227-11 lub skorzystaj z programu do obliczania sprężyn Gutekunst WinFSB na stronie www.federnshop.com, aby bezpłatnie obliczyć sprężyny naciskowe, sprężyny naciągowe i sprężyny skrętne.
Dodatkowe informacje: