Nachfolgend lesen Sie die Zusammenfassung der Grundlagen zur Federauslegung von Druckfedern, Zugfedern und Schenkelfedern.
 Technische Federn sind auch heute noch eines der wichtigsten Maschinenelemente und werden in Fahrzeugen, feinmechanischen oder elektrotechnischen Apparaten, medizinischen Geräten, Haushaltgeräten u.v.m. erfolgreich eingesetzt. Häufig hängt vom störungsfreien Arbeiten der Metallfeder die Funktion des gesamten Geräts oder Maschinenteils ab.
Technische Federn sind auch heute noch eines der wichtigsten Maschinenelemente und werden in Fahrzeugen, feinmechanischen oder elektrotechnischen Apparaten, medizinischen Geräten, Haushaltgeräten u.v.m. erfolgreich eingesetzt. Häufig hängt vom störungsfreien Arbeiten der Metallfeder die Funktion des gesamten Geräts oder Maschinenteils ab.
Metallfedern sind Elemente, die sich unter Belastung gezielt verformen und bei Entlastung wieder die ursprüngliche Gestalt annehmen. Dabei wird zugeführte Energie in Federarbeit (W) umgewandelt und zu einem späteren Zeitpunkt wieder abgegeben (Kraftspeicher). Diese Verformung und Energieaufnahme leistet die Metallfedern jedoch nur zuverlässig in dafür ausgelegten Grenzen. Deshalb ist die richtige Federauslegung und Federberechnung ein wichtiger Bestandteil für die perfekt arbeitende Metallfeder.
Table of Contents
Die Federkennlinie
Metallfedern oder technische Federn werden nach Ihrer Federkennlinie beurteilt. Diese Federkennlinie stellt die Abhängigkeit der Federkraft (F) vom Federweg (s) dar. Denn je nachdem, welche Federkennlinie gefordert ist (linear, progressiv, degressiv oder kombiniert), ändern sich auch Gestalt und Art der Feder.
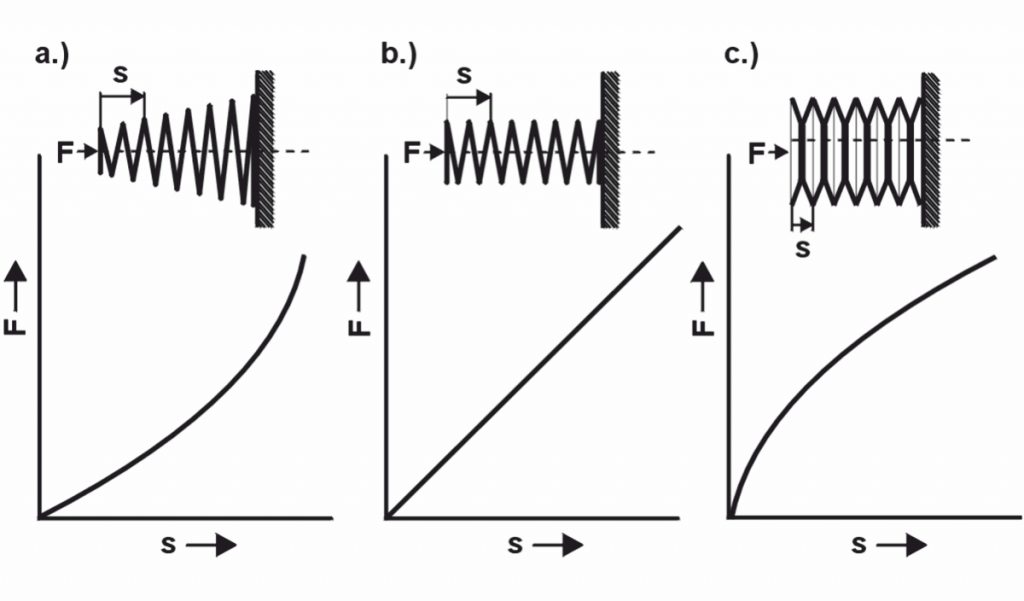
Mit der Federrate (R) wird die Federkennlinie im Federdiagramm bestimmt. Die Federrate (R) ist somit ein wichtiger Wert bei der Federauslegung zur passenden Feder. Bei linearer Federkennlinie ist die Federrate konstant. Federn mit gekrümmter Federkennlinie besitzen eine veränderliche Federrate. Bei einer linearen Kennlinie gelten daher nachfolgende Formeln:
für Druck- und Zugfedern
R=\frac{F2-F1}{s2-s1}für Schenkel- und Drehfedern
R_{M}=\frac{M2-M1}{\alpha2-\alpha1}
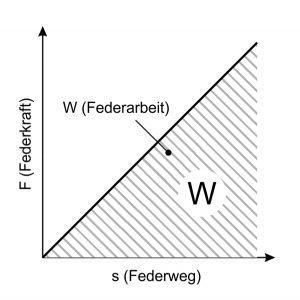
Die Federarbeit
Beim Spannen der Metallfeder wird Arbeit verrichtet, die dann beim Entspannen wieder abgegeben wird. Die Federarbeit (W) ergibt sich stets als Fläche unterhalb der Federkennlinie. Bei linearer Federkennlinie gilt somit:
für Druck- und Zugfedern
W=\frac{1}{2}F\cdot sfür Schenkel- und Drehfedern
W=\frac{1}{2}M\cdot \alphaDurch die Berechnung des Volumennutzwerts lassen sich verschiedene Federarten über das Verhältnis von Federarbeit (W) und Bauraum (V) miteinander vergleichen:
\eta_{A}=\frac{W}{V}
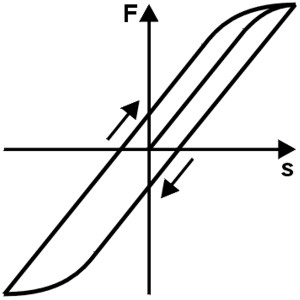
Die Hysterese
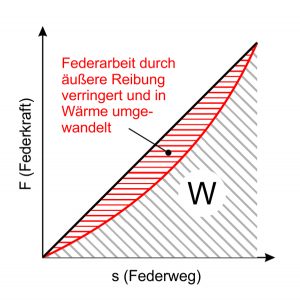
Das Federungsverhalten kann durch äußere Reibung beeinflusst werden. Diese Reibungskräfte behindern die Rückverformung der Feder. Bei einer Wechselbeanspruchung äußert sich dies in Form einer Hystereseschleife. Ein Teil der Federarbeit wird dabei durch die Reibung in Wärme umgewandelt und geht dann „verloren“. Da dies beim Einsatz von Federn unerwünscht ist, sollte jegliche Reibung konstruktiv durch Anordnung und Gestalt der Federn vermieden werden.
Die Relaxation
Wenn beispielsweise eine Druckfeder bei höherer Temperatur zwischen parallelen Platten auf eine bestimmte Länge zusammengedrückt wird, so kann man feststellen, dass die Federkraft mit der Zeit allmählich abnimmt. Dieser Kraftverlust nimmt mit steigender Temperatur und Spannung zu.
Relaxation des Werkstoffs ist eine plastische Verformung, die sich bei konstanter Einbaulänge als Kraftverlust äußert. Dieser wird prozentual bezogen auf die Ausgangskraft F1 angegeben:
Relaxation=\frac{\Delta F\cdot 100}{F1}Den prinzipiellen Verlauf der Relaxation und der Relaxationsgeschwindigkeit zeigt das nachfolgende Diagramm:
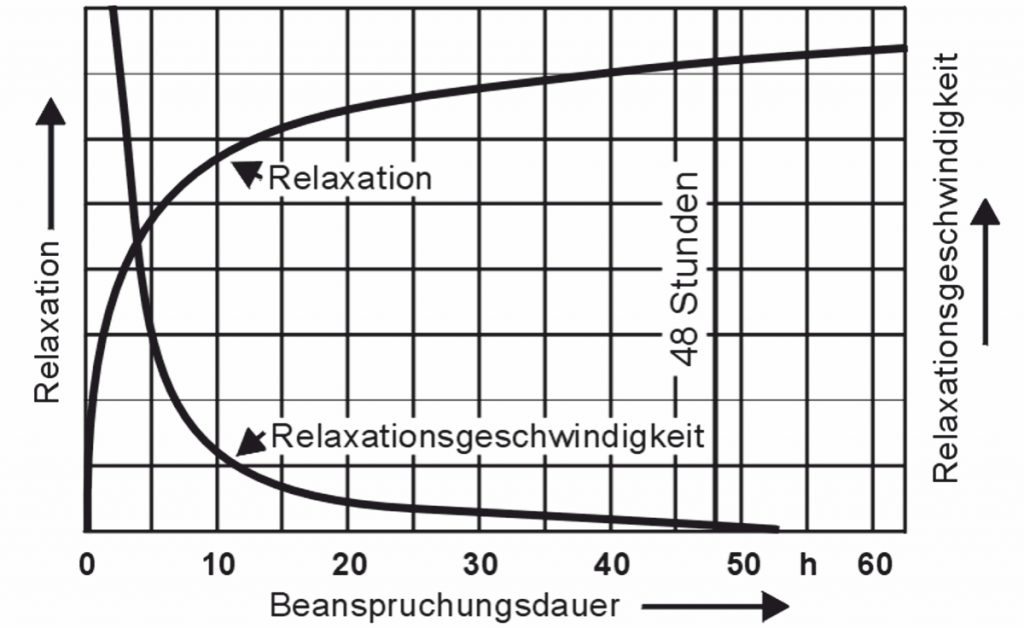
Die Relaxationswerte nach 48 Stunden gelten als Kennwerte, obwohl zu diesem Zeitpunkt die Relaxation noch nicht völlig abgeschlossen ist. In der EN 13906-1 findet man werkstoffabhängige Relaxationsschaubilder. Diese sind nur dann vom Konstrukteur einzubeziehen, falls hohe Anforderungen an die Konstanz der Federkraft gestellt werden. Die Relaxation bei verschiedenen Temperaturzuständen wird bei der Berechnung im Federnberechnungsprogramm WinFSB von Gutekunst Federn, aufrufbar unter www.federnshop.com, mit ausgewiesen.
Die richtige Federwerkstoffauswahl
Metallfedern müssen aus einem geeigneten Federwerkstoff hergestellt und so ausgelegt und gestaltet werden, dass sie nach Wegnahme einer aufgebrachten Belastung wieder ihre ursprüngliche Gestalt erreichen. Zum Ausdruck kommt diese Eigenschaft im Elastizitätsmodul und im Gleitmodul. Diese Werkstoffkenngrößen drücken das Verhältnis zwischen Spannung und Dehnung aus und sollten einen möglichst hohen Wert aufweisen.
Außerdem sollen Federwerkstoffe:
- hohe Elastizitätsgrenzen, d. h. einen großen rein elastischen Bereich haben,
- die entsprechenden Spannungen auch bei erhöhten Temperaturen ohne größere Kraftverluste ertragen (geringe Relaxation),
- eine hohe Dauerschwingfestigkeit aufweisen (feinkörniges Gefüge, frei von Verunreinigungen),
- ein ausreichendes Verformungsvermögen haben,
- eine möglichst gleitfähige Oberfläche besitzen,
- bestimmten Anforderungen an den Korrosionsschutz standhalten,
- elektrisch leitend oder unmagnetisch sein.
Elastizitäts- und Gleitmodule verschiedener Federwerkstoffe
| Federwerkstoff | E-Modul [N/mm²] | G-Modul [N/mm²] |
| Patentiert gezogener Federstahldraht nach EN 10270-1 | 206000 | 81500 |
| Ölschlussvergüteter Ventilfederdraht nach EN 10270-2 | 206000 | 81500 |
| Warmgewalzter Stahl nach EN10089 | 206000 | 78500 |
| Kaltband nach EN 10132 | 206000 | 78500 |
| X10 CrNi 18 8 (1.4310) | 185000 | 70000 |
| X7 CrNiAl 17 7 (1.4568) | 195000 | 73000 |
| X5 CrNiMo 17-12-2 (1.4401) | 180000 | 68000 |
| CuSn6 R950 nach EN 12166 | 115000 | 42000 |
| CuZn36 R700 nach EN 12166 | 110000 | 39000 |
| CuBe2 nach EN 12166 | 120000 | 47000 |
| CuNi18Zn20 nach EN 12166 | 135000 | 45000 |
| CuCo2Be nach EN 12166 | 130000 | 48000 |
| Inconel X750 | 213000 | 76000 |
| Nimonic 90 | 213000 | 83000 |
| Hastelloy C4 | 210000 | 76000 |
| Titanlegierung TiAl6V4 | 104000 | 39000 |
Einfluss der Arbeitstemperatur bei der Federwerkstoffauswahl
Verhalten bei erhöhten Arbeitstemperaturen
Die Höhe der Arbeitstemperatur kann die Funktion einer Feder erheblich beeinflussen, da die Neigung zu Relaxation mit steigender Temperatur zunimmt. Nach Auswertung der Relaxationsschaubilder können für die wichtigsten Federwerkstoffe folgende Grenztemperaturen angesetzt werden.
Grenztemperaturen von Federwerkstoffen bei minimaler Relaxation
| Federwerkstoff | Maximale Arbeitstemperatur in °C bei | |
| hoher Belastung | niedriger Belastung | |
| Patentiert gezogener Federstahldraht nach EN 10270-1 | 60-80 | 80-150 |
| Ölschlussvergüteter Ventilfederdraht nach EN 10270-2 | 80-160 | 120-160 |
| X10CrNi 18.8 (1.4310) | 160 | 250 |
| X7CrNiAl 17.7 (1.4568) | 200 | 350 |
| X5CrNiMo 17-12-2 (1.4401) | 160 | 300 |
| CuSn6 | 80 | 100 |
| CuZn36 | 40 | 60 |
| CuBe2 | 80 | 120 |
| CuNi18Zn20 | 80 | 120 |
| Inconel X750 | 475 | 550 |
| Nimonic90 | 500 | 500 |
Außerdem nehmen die für die Federfunktion wichtigen Werkstoffeigenschaften Elastizitätsmodul und Schubmodul mit steigender Temperatur ab. Sowohl das Schubmodul als auch der Elastizitätsmodul werden bei höherer Temperatur nach folgender Formel ermittelt, wobei die Werkstoffkennwerte bei Raumtemperatur (20°C) als Basis dienen.
G_{t}=G_{20}=\frac{3620-T}{3600}bzw.
E_{t}=E_{20}=\frac{3620-T}{3600}
Damit ist es dem Konstrukteur möglich, die tatsächlichen Federkräfte bei der voraussichtlichen Betriebstemperatur zu bestimmen.
Verhalten bei tiefen Betriebstemperaturen
Beim Einsatz in Kühlanlagen, im Weltraum oder bei starker winterlicher Kälte müssen teilweise Temperaturen bis zu – 200 ° ertragen werden. Trotz steigender Zugfestigkeit wirken sich tiefe Temperaturen ungünstig aus, da die Zähigkeit der Werkstoffe abnimmt und Sprödbrüche auftreten können. Nichtrostende Federstähle sowie Kupfer- und Nickellegierungen sind beim Tieftemperatureinsatz den patentierten Federdrähten sowie den Ventilfederdrähten vorzuziehen. Nachfolgende Tabelle zeigt die Grenztemperaturen auf.
Empfehlungen für den Tieftemperatureinsatz
| Federwerkstoff | Minimale Arbeitstemperatur in °C |
| Patentiert gezogener Federstahldraht nach EN 10270-1 | -60 |
| Ölschlussvergüteter Ventilfederdraht nach EN 10270-2 | -60 |
| X10CrNi 18.8 (1.4310) | -200 |
| X7CrNiAl 17.7 (1.4568) | -200 |
| X5CrNiMo 17-12-2 (1.4401) | -200 |
| CuSn6 | -200 |
| CuZn36 | -200 |
| CuBe2 | -200 |
| CuNi18Zn20 | -200 |
| Inconel X750 | -100 |
| Nimonic90 | -100 |
Verwendung Federsysteme
Aus konstruktiven Gründen ist es auch möglich, mehrere Federn zur Aufnahme von Kräften und Bewegungen einzusetzen. Einfache Federsysteme sind Parallel– und Reihenschaltungen.
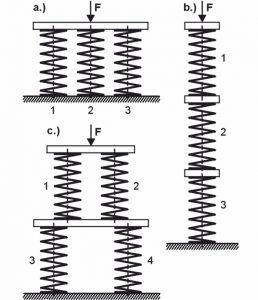
a) Parallelschaltung
Die Federn werden so angeordnet, dass sich die äußere Belastung (F) anteilmäßig auf die einzelnen Federn aufteilt, aber der Weg der einzelnen Federn gleich groß ist. So ergibt sich:
s=s1=s2=s3=... (Gesamtfederweg)
F=F1+F2+F3+... (Gesamtfederkraft)
R=R1+R2+R3+... (Gesamtfederrate)
Die Federrate des Gesamtsystems einer Parallelschaltung ist stets größer als die Federrate der Einzelfedern
b) Reihenschaltung
Die Federn sind hintereinander angeordnet, so dass auf jede Feder die gleiche Kraft wirkt, der Federweg sich jedoch auf die Einzelfedern aufteilt. Es ergibt sich:
s=s1+s2+s3+... (Gesamtfederweg)
F=F1=F2=F3=... (Gesamtfederkraft)
R=\frac{1}{\frac{1}{R1}+\frac{1}{R2}+\frac{1}{R3}+...} (Gesamtfederrate)
Die Federrate des Gesamtsystems einer Reihenschaltung ist stets kleiner als die Federrate der Einzelfedern
c) Mischschaltung
Es werden mehrere Federn parallel und hintereinander geschaltet. Wegen des Gleichgewichts müssen R1=R2 und R3=R4 sein. Für den dargestellten Fall gilt:
R=\frac{1}{\frac{1}{R1+R2}+\frac{1}{R3+R4}+...} (Gesamtfederrate)
Die Federrate des Gesamtsystems der gezeigten Mischschaltung liegt zwischen kleinster und größter Federrate der Einzelfedern!
Im zweiten Teil der Informationsserie „Auslegung Metallfeder – Teil 2 „Berechnung“ stellen wir Ihnen die Berechnungsparameter für den Funktions- und Festigkeitsnachweis der Druckfedern, Zugfedern und Schenkelfedern vor.
Sollten Sie Bedarf an einer individuellen Federauslegung haben, so mailen Sie uns einfach die Eckdaten der benötigten Metallfeder an service@federnshop.com , kontaktieren unsere Technik per Telefon unter (+49) 035877 227-11 oder verwenden Sie unter www.federnshop.com das Gutekunst Federnberechnungsprogramm WinFSB zur freien Berechnung von Druckfedern, Zugfedern und Schenkelfedern.
Weitere Informationen: