En la primera parte de esta serie de dos, Gutekunst Federn proporcionó información sobre los fundamentos del diseño de muelles. En esta segunda parte encontrarás los datos de cálculo específicos para el diseño de muelles de compresión, muelles de tracción y muelles de torsión (resortes de torsión). El programa de cálculo de muelles Gutekunst WinFSB también está disponible para cálculos individuales.
El objetivo del diseño de un muelle de compresión, tracción o torsión es encontrar el muelle más económico para la tarea encomendada, teniendo en cuenta todas las circunstancias, que además se ajuste al espacio disponible y alcance la vida útil requerida. Además de estos requisitos de fabricación y materiales, el diseño correcto del muelle es especialmente importante.
Antes de calcular el muelle, hay que recopilar los siguientes requisitos del muelle metálico:
1. tipo de carga (estática o dinámica)
2. De por vida
3. Temperatura de funcionamiento
5. Fuerzas requeridas y recorrido del muelle
6. espacio de instalación disponible
7. tolerancias(muelles de compresión, muelles de tracción)
8. situación de la instalación (pandeo, suspensión transversal)
Cada cálculo de muelle consta de dos etapas:
- Prueba de funcionamiento: comprobación del índice de elasticidad, fuerzas y recorrido del muelle, comportamiento ante vibraciones, etc.
- Verificación de la resistencia
Comprobación del cumplimiento de las tensiones admisibles o prueba de la resistencia a la fatiga.
Esto requiere un enfoque iterativo.
La verificación de la resistencia se basa en la decisión de si el muelle está sometido a una carga estática, cuasiestática o dinámica. Deben utilizarse los siguientes criterios para la diferenciación:
- Carga estática o cuasiestática: carga constante (estática) en el tiempo o carga variable en el tiempo con menos de 10.000 carreras en total.
- Tensión dinámica: cargas variables en el tiempo con más de 10.000 golpes. El muelle suele estar pretensado y sometido a cargas periódicas de hinchamiento con una curva sinusoidal, que se producen aleatoriamente (estocásticamente), por ejemplo, en las suspensiones de los vehículos de motor. En algunos casos, se producen cambios bruscos de fuerza.
Al dimensionar los muelles, hay que definir los límites de carga basándose en los valores de resistencia de los materiales y teniendo en cuenta el tipo de carga. Se incluye un factor de seguridad para determinar la tensión admisible. Tras una comparación con la tensión real presente, el dimensionamiento del muelle debe revisarse mediante un procedimiento iterativo. Se aplica lo siguiente: Tensión nominal ≤ Tensión admisible
Table of Contents
Cálculo de muelles de compresión
Información general
Los muelles de compresión cilíndricos conformados en frío con paso constante son los más utilizados en la práctica. El alambre se forma en frío enrollándolo alrededor de un mandril. La distancia entre las espiras y el contacto del muelle se regulan en función del avance del pasador de paso. Tras el enrollado, se lleva a cabo el templado para reducir las tensiones residuales en el muelle y aumentar el límite de elasticidad al cizallamiento. Por tanto, la cantidad de ajuste se reduce. Las temperaturas y los tiempos de revenido dependen del material; el enfriamiento tiene lugar en el aire a temperatura ambiente normal.
Otras operaciones importantes en la producción de muelles son la molienda y el fraguado. Los extremos del muelle suelen rectificarse a partir de un grosor de alambre de 0,5 mm para garantizar un apoyo plano-paralelo del muelle y una transmisión óptima de la fuerza.
Si el esfuerzo cortante supera el valor admisible cuando el muelle está cargado, se produce una deformación permanente, que se manifiesta en la reducción de la longitud no tensada. Este proceso se denomina «fraguado» en la tecnología de los muelles, lo que equivale a los términos «fluencia» y«relajación» de la tecnología de los materiales. Para contrarrestarlo, los muelles de compresión se enrollan más largos en la cantidad de ajuste prevista y después se comprimen hasta la longitud de bloqueo. Este preajuste permite un mejor aprovechamiento del material y permite una mayor carga en su uso posterior.
Fórmulas de cálculo muelle de compresión cilíndrico
El cálculo del muelle de compresión se basa en las ecuaciones de cálculo de la norma DIN EN 13906-1:
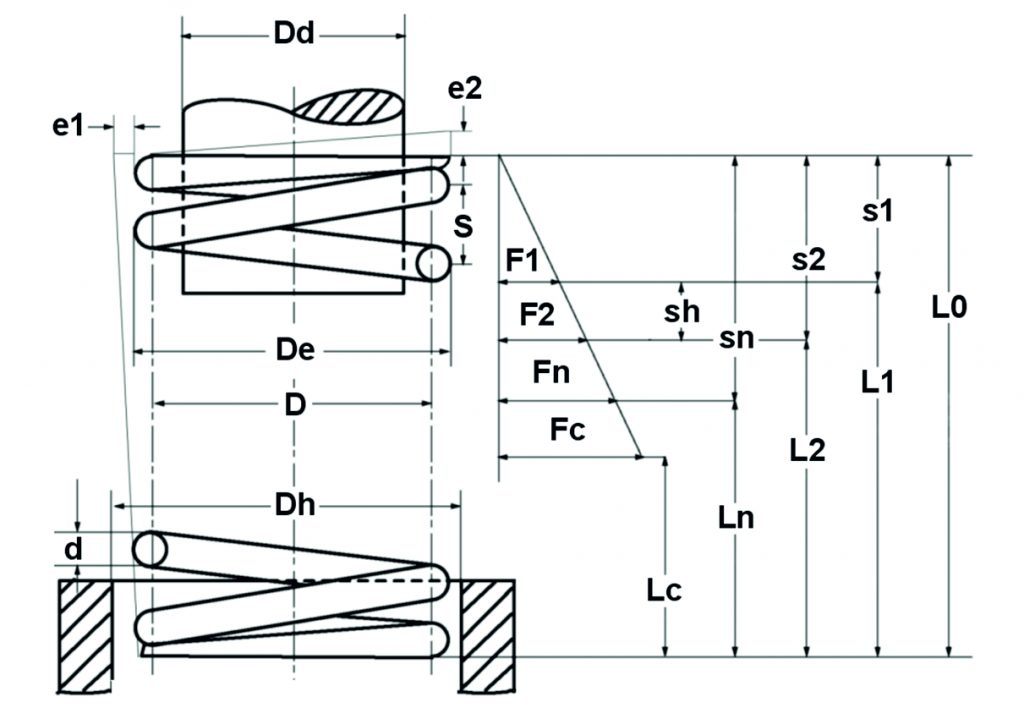
Figura: Esquema teórico del muelle de compresión
Prueba de funcionamiento de los muelles de compresión
Lo siguiente se aplica a los muelles de compresión cilíndricos fabricados con alambre de sección circular:
Fórmula del índice de elasticidad: \Large R=\frac{ Gd^{4}}{8D^{3}n}
se deduce de R=F/s:
Fuerza de la primavera : \Large F=\frac{ Gd^{4}s}{8D^{3}n}
y:
Recorrido de suspensión : \Large s=\frac{8D^{3}nF}{Gd^{4}}
Verificación de la resistencia del muelle de compresión
Una vez determinadas las dimensiones del resorte, se debe verificar la resistencia. Para ello se determina el esfuerzo cortante existente:
Tensión de la fuerza: \Large \tau=\frac{8DF}{\pi d^{3}}
Tensión de la trayectoria: \Large \tau=\frac{Gds}{\pi n D^{2}}
Mientras que el esfuerzo cortante τ se utiliza para el diseño de muelles sometidos a esfuerzos estáticos o cuasiestáticos, el esfuerzo cortante corregido τk se aplicaa los muelles sometidos a esfuerzos dinámicos. La distribución del esfuerzo cortante en la sección transversal del alambre de un resorte es desigual, el esfuerzo más alto ocurre en el diámetro interno del resorte. Con el factor de corrección de tensión k, que depende de la relación de bobinado (relación entre el diámetro medio y el grosor del alambre) del resorte, se puede determinar aproximadamente la tensión más alta. En los muelles de compresión sometidos a esfuerzos dinámicos, esto se traduce en
Esfuerzo cortante corregido: \Large \tau_{k}=k\tau
donde se aplica lo siguiente a k (según Bergsträsser):
\Large k=\frac{\frac{D}{d}+0,5}{\frac{D}{d}-0,75}Ahora la comparación se realiza con la tensión admisible. Esto se define de la siguiente manera:
Voltaje admisible:
\Large \tau_{{zul}}=0,5 \cdot R_{{m}}y
\Large \tau_{{czul}}=0,56 \cdot R_{{m}}Los valores para elResistencia mínima a la tracción R m dependen del grosor del alambre y se pueden encontrar en las normas de los materiales correspondientes.
Como regla general, debe ser posible comprimir los resortes de compresión hasta la longitud del bloque, por lo que la tensión admisible en la longitud del bloque es t czul considerar.
A estrés dinámico debe voltaje inferior y superior (tk1 y tk2) de la carrera correspondiente se puede determinar. La diferencia es el voltaje de carrera. Tanto la tensión superior como la tensión de carrera no deben superar los valores admisibles correspondientes. Puedes encontrarlos en los diagramas de resistencia a la fatiga de la norma EN 13906-1:2002. Si las tensiones resisten esta comparación, el resorte es resistente a la fatiga con un ciclo de carga límite de 107.
Relaciones geométricas para muelles de compresión
| Característica de la primavera | Ecuación de cálculo |
| Número total de bobinados | nt = n + 2 |
| Longitud del bloque del muelle de tierra | Lc = nt dmax |
| Longitud del bloque del muelle sin cortar | Lc = (nt + 1,5)dmax |
| Longitud útil más pequeña | Ln = Lc + Sa |
| Longitud sin tensión | L0 = Ln + sn |
| Suma de las distancias mínimas entre los arrollamientos | \Large S_{a}=\left (0,0015 \frac{D^{2}}{d} + 0,1d \right )\cdot n |
| Aumento del diámetro exterior bajo carga
terreno de juego |
\Large \triangle D_{e}=0,1 \frac{S^{2}-08Sd-0,2d^{2}}{D}
\Large S=\frac{L0-d}{n} (suelo) \Large S=\frac{L0-2,5d}{n} (sin pulir)
|
|
Deformación del muelle de pandeo (válida para varios coeficientes de apoyo n, ver EN 13906-1:2002) |
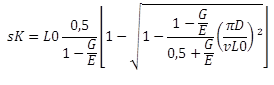 |
Todos los muelles sometidos a esfuerzos dinámicos con un grosor de alambre de > 1 mm deben granallarse. Esto aumenta la fuerza del golpe continuo. Una vez realizadas tanto la verificación funcional como la verificación de resistencia, hay que realizar y tener en cuenta diversos cálculos geométricos para poder encajar el muelle en el diseño del componente. La longitud del bloque no se puede rebajar porque los arrollamientos están firmemente conectados entre sí, la menor longitud utilizable no se debe rebajar porque entonces ya no se garantiza una curva de fuerza lineal ni la capacidad de carga dinámica. También deben tenerse en cuenta las tolerancias admisibles según la norma DIN 2095.
Cálculo de muelles de tracción
Información general
Los muelles de extensión se enrollan alrededor de un mandril exactamente igual que los muelles de compresión, pero sin distancia entre las espiras y con diferentes formas de ojales/extremos para fijar el muelle. En el proceso de producción, los arrollamientos se presionan estrechamente entre sí. Esta pretensión interna F0 depende de la relación de bobinado y no puede acabarse a cualquier nivel deseado. El software de cálculo WinFSB de Gutekunst Federn proporciona valores de referencia para el nivel de precarga tras introducir los datos relevantes del muelle.
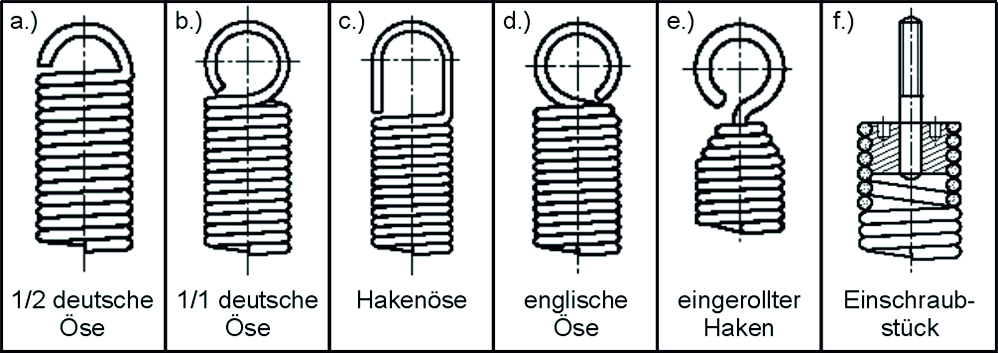
Imagen: Formas comunes de los ojales: a.) Medio ojal alemán; b.) ojal alemán entero; c.) Ojo de gancho; d.) Ojal inglés; e.) gancho enrollado; f.) Pieza atornillable
La ventaja de los muelles de tracción es que no se retuercen; las desventajas son el mayor espacio de instalación y la interrupción total del flujo de fuerza cuando se rompe el muelle.
Fórmulas de cálculo muelle de tracción cilíndrico
De acuerdo con las ecuaciones de cálculo de los muelles de compresión, pero teniendo en cuenta la fuerza de precarga, las siguientes relaciones se aplican a los muelles de tracción cilíndricos de alambre redondo (ver también la figura 1.8):
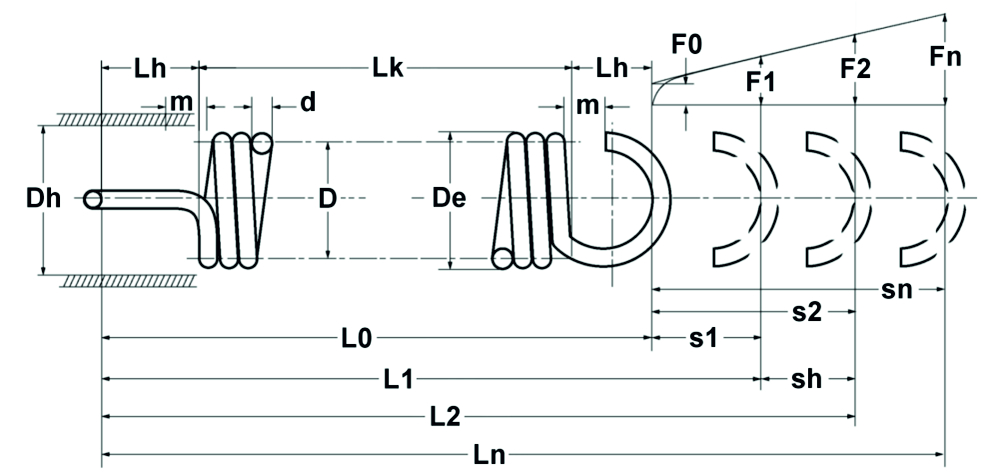
Figura: Diagrama teórico del muelle de tracción
Prueba de la función del muelle de tracción
Lo siguiente se aplica a los muelles de tracción cilíndricos fabricados con alambre de sección circular:
Índice de elasticidad: \Large R=\frac{Gd^4}{8D^3n}=\frac{F-F0}{s}
se deduce de R=F/s:
Fuerza del muelle: \Large F=\frac{Gd^4s}{8D^3n}+F0
y:
Recorrido del muelle: \Large s=\frac{8D^3n(F-F0)}{Gd^4}
Verificación de la resistencia de los muelles de tracción
Al igual que en los cálculos de muelles de compresión, hay que determinar el esfuerzo cortante existente.
Esfuerzo cortante: \Large \tau=\frac{8DF}{\pi d^3}
El esfuerzo de elevación corregido también debe calcularse para las cargas dinámicas.
Esfuerzo cortante corregido: \Large \tau_{{k}}=k\tau
Tensión admisible: \Large \tau_{zul}=0,45 \cdot R_{{m}}
La tensión máxima existente \tautn para los viajes más grandes sn está ajustado a la tensión permitida. Sin embargo, para evitar la relajación, en la práctica sólo debe utilizarse el 80 % de este recorrido de suspensión.
\Large s_{{2}}=0,8 \cdot s_{{n}}No pueden especificarse valores de resistencia a la fatiga de aplicación general para cargas dinámicas, ya que pueden producirse tensiones adicionales en los puntos de flexión de los ojales, algunas de las cuales pueden superar las tensiones admisibles. Por tanto, los muelles de tracción sólo deben someterse a cargas estáticas si es posible. Si no se puede evitar el estrés dinámico, se debe optar por Ojales prescindir y utilizar piezas terminales enrolladas o atornilladas. Una prueba de vida en condiciones de funcionamiento posteriores tiene sentido. A Endurecimiento superficial por granallado no es factible debido a las curvas cerradas.
Relaciones geométricas de los muelles de tracción
| Característica de la primavera | Ecuación de cálculo |
| Longitud del cuerpo | LK = (nt + 1)d |
| Longitud sin tensión | L0 = LK + 2 LH |
| Altura del ojal medio ojal alemán | LH = 0,55Di a 0,80Di |
| Altura del ojal ojal alemán entero | LH = 0,80Di a 1,10Di |
| Altura del ojal Ojal del gancho | LH > 1,10Di |
| Altura del ojal Ojal inglés | LH = 1,10Di |
Deben respetarse las tolerancias de fabricación admisibles según la norma DIN 2097.
Cálculo de muelles de torsión (muelles de torsión)
Información general
Los muelles de brazos cilíndricos enrollados (muelles de torsión) tienen esencialmente la misma forma que los muelles cilíndricos de compresión y extensión, a excepción de los extremos del muelle. Se doblan en forma de pata para permitir que el cuerpo del muelle gire alrededor de su eje. Esto significa que existen muchos campos de aplicación, por ejemplo, como muelles de retorno o muelles de bisagra. El muelle de torsión debe montarse sobre un mandril guía y la carga sólo debe aplicarse en la dirección de enrollado. Esto reduce el diámetro interior. Los muelles suelen enrollarse sin paso. Sin embargo, si la fricción es absolutamente indeseable, los muelles de torsión también pueden fabricarse con separación entre espiras. En caso de cargas dinámicas, hay que procurar que no haya dobleces de bordes afilados en los extremos de los muelles, para evitar picos de tensión imprevisibles.
Fórmulas de cálculo para muelles de torsión cilíndricos (muelles de torsión)
El cálculo se realiza de acuerdo con las directrices de la norma EN 13906-3:2001:
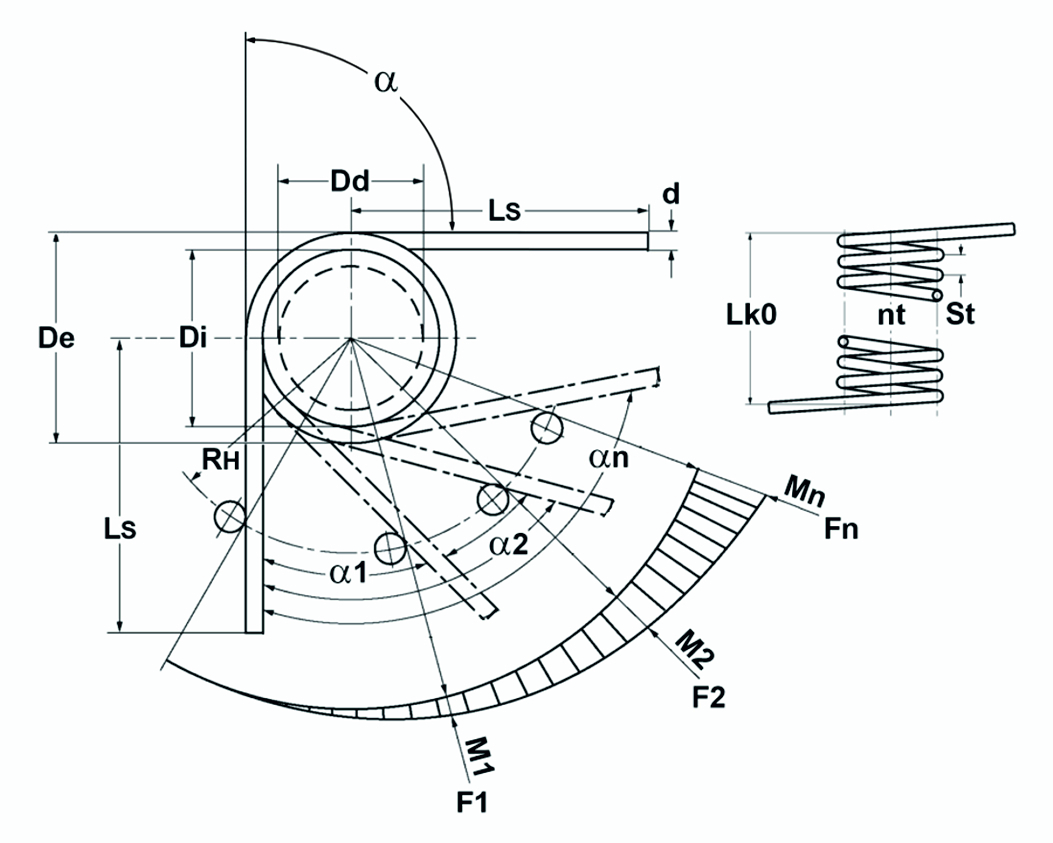
Figura: Esquema teórico del muelle de torsión / muelle de torsión
Verificación funcional de muelles de torsión (resortes de torsión)
Federmomentrato: \Large R_{M}=\frac{M}{\alpha}=\frac{d^4E}{3667Dn}
Momento de la primavera: \Large M=FR_{H}=\frac{d^4E\alpha}{3667Dn}
Ángulo de rotación: \Large \alpha=\frac{3667DMn}{Ed^4}
Verificación de la resistencia de los muelles de torsión (resortes de torsión)
Se determina la tensión de flexión existente y se compara con la tensión admisible. En el caso de la tensión dinámica, debe utilizarse de nuevo la tensión corregida para la comparación.
Esfuerzo de flexión: \Large \sigma=\frac{32M}{\pi d^3}
Tensión de flexión corregida: \Large \sigma_{{q}}=q \sigma
donde q es válido:
\Large q=\frac{\frac{D}{d}+0,07}{\frac{D}{d}-0,75}
Esfuerzo de flexión admisible: \Sigma_{{zul}}=0,7Rm
A estrés dinámico debe voltaje inferior y superior (tk1 y tk2) de la carrera correspondiente se puede determinar. La diferencia es el voltaje de carrera. Tanto la tensión superior como la tensión de carrera no deben superar los valores admisibles correspondientes. Para el alambre de acero para muelles, se pueden encontrar en los diagramas de resistencia a la fatiga de la norma EN 13906-3:2001. Si las tensiones resisten esta comparación, el resorte es resistente a la fatiga con un ciclo de carga límite de 107 .
Relaciones geométricas para muelles de torsión (resortes de torsión)
| Característica de la primavera | Ecuación de cálculo |
| Reducción del diámetro interior con carga máxima | \Large Di_{n}=\frac{Dn}{n+\frac{\alpha}{360}}-d |
| Longitud del cuerpo sin carga | \Large Lk=(n+1,5)d |
| Longitud del cuerpo bajo carga máxima | \Large Lk_{n}=(n+1,5+\frac{\alpha}{360})d |
| Viaje de primavera | \Large s_{n}= \frac{\alpha_{n}R_{H}}{57,3} |
Además, hay que tener en cuenta las tolerancias de fabricación según la norma DIN 2194.
También puedes descargarte un resumen del artículo «Diseño de un muelle metálico», que consta de la Parte 1 «Conceptos básicos» y la Parte 2 «Cálculo», en Gutekunst Federn 1×1.
Si necesitas un diseño de muelle personalizado, sólo tienes que enviarnos por correo electrónico los datos clave del muelle metálico que necesitas a technik@gutekunst-co.com, ponerte en contacto con nuestro departamento técnico por teléfono en el (+49) 035877 227-11 o utilizar el programa de cálculo de muelles Gutekunst WinFSB en https://www.federnshop.com para calcular gratuitamente muelles de compresión, extensión y torsión.
Información Adicional: