Nella prima parte di questa serie in due parti, Gutekunst Federn ha fornito informazioni sulle basi del design delle molle. In questa seconda parte troverai i dati di calcolo specifici per la progettazione di molle a compressione, molle a trazione e molle a torsione (molle di torsione). Il programma di calcolo delle molle WinFSB di Gutekunst è disponibile anche per calcoli individuali.
L’obiettivo della progettazione di una molla a compressione, a trazione o a torsione è quello di trovare la molla più economica per il compito da svolgere, tenendo conto di tutte le circostanze, che si adatti allo spazio disponibile e che raggiunga la durata richiesta. Oltre a questi requisiti di produzione e di materiale, il corretto design della molla è particolarmente importante.
Prima di calcolare la molla, è necessario tenere conto dei seguenti requisiti della molla metallica:
1. tipo di carico (statico o dinamico)
2. Vita
5. Forze richieste e corsa della molla
6. spazio di installazione disponibile
7. tolleranze(molle a compressione, molle a trazione)
8. situazione di installazione (instabilità, sospensione trasversale)
Ogni calcolo della molla è composto da due fasi:
- Prova di funzionamento: verifica della velocità della molla, delle forze e della corsa della molla, del comportamento alle vibrazioni, ecc.
- Verifica della resistenza
Verifica il rispetto delle sollecitazioni consentite o la prova di resistenza alla fatica.
Ciò richiede un approccio iterativo.
La verifica della resistenza si basa sulla decisione di sottoporre la molla a un carico statico, quasi statico o dinamico. I criteri di differenziazione da utilizzare sono i seguenti:
- Carico statico o quasi statico: carico costante (statico) nel tempo o carico variabile nel tempo con meno di 10.000 corse in totale.
- Sollecitazioni dinamiche: carichi variabili nel tempo con più di 10.000 corse. La molla è solitamente pretensionata e sottoposta a carichi periodici di rigonfiamento con una curva sinusoidale, che si verificano in modo casuale (stocastico), ad esempio nelle sospensioni dei veicoli a motore. In alcuni casi si verificano bruschi cambiamenti di forza.
Quando si dimensionano le molle, i limiti di carico devono essere definiti in base ai valori di resistenza dei materiali e tenendo conto del tipo di carico. Un fattore di sicurezza è incluso per determinare la tensione ammissibile. Dopo un confronto con le sollecitazioni reali presenti, il dimensionamento della molla deve essere rivisto con una procedura iterativa. Vale quanto segue: Tensione nominale ≤ tensione ammissibile
Table of Contents
Calcolo delle molle a compressione
Informazioni generali
Le molle a compressione cilindriche formate a freddo con passo costante sono le più utilizzate nella pratica. Il filo viene formato a freddo avvolgendolo intorno a un mandrino. La distanza tra le spire e il contatto della molla sono regolati in base alla velocità di avanzamento del perno del passo. Dopo l’avvolgimento, si procede al rinvenimento per ridurre le tensioni residue nella molla e aumentare il limite di elasticità a taglio. L’importo dell’impostazione viene quindi ridotto. Le temperature e i tempi di rinvenimento dipendono dal materiale; il raffreddamento avviene in aria alla normale temperatura ambiente.
Altre operazioni importanti nella produzione di molle sono la molatura e l’incastonatura. Le estremità della molla sono solitamente rettificate con uno spessore del filo di 0,5 mm per garantire un appoggio piano-parallelo della molla e una trasmissione ottimale della forza.
Se lo sforzo di taglio supera il valore consentito quando la molla è caricata, si verifica una deformazione permanente che si manifesta con una riduzione della lunghezza non sollecitata. Nella tecnologia delle molle, questo processo viene definito “presa”, che può essere equiparato ai termini “scorrimento” e“rilassamento” della tecnologia dei materiali. Per ovviare a questo inconveniente, le molle di compressione vengono avvolte più a lungo della quantità di regolazione prevista e successivamente compresse fino alla lunghezza del blocco. Questa preimpostazione consente un migliore utilizzo del materiale e permette di ottenere un carico maggiore in un secondo momento.
Formule di calcolo molla a compressione cilindrica
Il calcolo della molla a compressione si basa sulle equazioni di calcolo della norma DIN EN 13906-1:
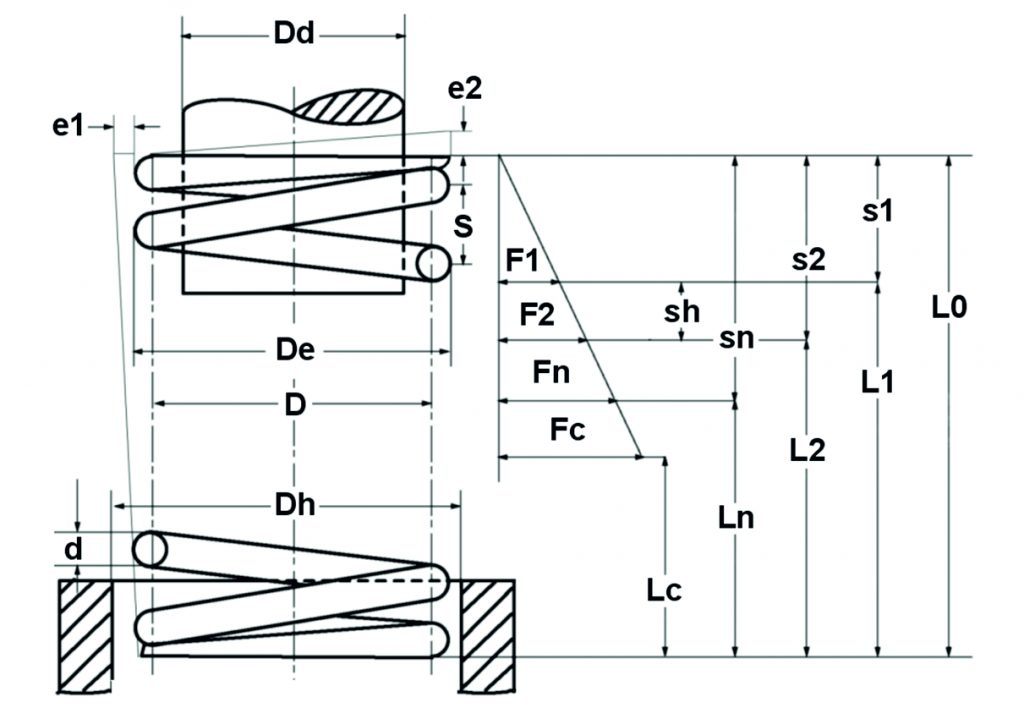
Figura: Diagramma teorico della molla a compressione
Prova di funzionamento delle molle a compressione
Quanto segue si applica alle molle a compressione cilindriche realizzate con fili a sezione circolare:
Formula della velocità della molla: \Large R=\frac{ Gd^{4}}{8D^{3}n}
segue da “R=F/s”:
Forza della molla : \Large F=\frac{ Gd^{4}s}{8D^{3}n}
e:
Corsa della sospensione : \Large s=\frac{8D^{3}nF}{Gd^{4}}
Verifica della resistenza della molla a compressione
Dopo aver determinato le dimensioni della molla, è necessario verificarne la resistenza. A questo scopo viene determinata la sollecitazione di taglio esistente:
Tensione da forza: \Large \tau=\frac{8DF}{\pi d^{3}}
Tensione dal percorso: \Large \tau=\frac{Gds}{\pi n D^{2}}
Mentre la sollecitazione di taglio τ viene utilizzata per la progettazione di molle sollecitate staticamente o quasi staticamente, la sollecitazione di taglio corretta τk si applicaalle molle sollecitate dinamicamente. La distribuzione della sollecitazione di taglio nella sezione trasversale del filo di una molla non è uniforme, la sollecitazione massima si verifica sul diametro interno della molla. Con il fattore di correzione della tensione k, che dipende dal rapporto di avvolgimento (rapporto tra diametro medio e spessore del filo) della molla, è possibile determinare approssimativamente la tensione massima. Per le molle di compressione sollecitate dinamicamente, ciò si traduce in
Sforzo di taglio corretto: \Large \tau_{k}=k\tau
dove per k vale quanto segue (secondo Bergsträsser):
\Large k=\frac{\frac{D}{d}+0.5}{\frac{D}{d}-0.75}Ora il confronto viene effettuato con la tensione consentita. Questo è definito come segue:
Tensione ammissibile:
\Large \tau_{{zul}}=0.5\cdot R_{{m}}e
\Large \tau_{{czul}}=0,56\cdot R_{{m}}I valori perResistenza alla trazione minima R m dipendono dallo spessore del filo e possono essere trovati negli standard dei materiali corrispondenti.
Di norma, deve essere possibile comprimere le molle di compressione fino alla lunghezza del blocco, motivo per cui la tensione ammissibile alla lunghezza del blocco è t czul considerare.
A stress dinamico deve abbassare e aumentare la tensione (tk1 e tk2) della corsa corrispondente può essere determinata. La differenza è la tensione della corsa. Sia la tensione superiore che la tensione della corsa non devono superare i corrispondenti valori ammessi. Questi possono essere trovati nei diagrammi di resistenza alla fatica della norma EN 13906-1:2002. Se le sollecitazioni resistono a questo confronto, la molla è resistente alla fatica con un ciclo di carico limite di 10 7 .
Relazioni geometriche per molle a compressione
| Caratteristica della primavera | Equazione di calcolo |
| Numero totale di avvolgimenti | nt = n + 2 |
| Lunghezza del blocco della molla a terra | Lc = nt dmax |
| Lunghezza del blocco della molla non tagliata | Lc = (nt + 1,5)dmax |
| Lunghezza minima utilizzabile | Ln = Lc + Sa |
| Lunghezza non sollecitata | L0 = Ln + sn |
| Somma delle distanze minime tra gli avvolgimenti | \Large S_{a}=\left (0,0015 \frac{D^{2}}{d} + 0,1d \right )\cdot n |
| Allargamento del diametro esterno sotto carico
intonazione |
\Large \triangle D_{e}=0.1\frac{S^{2}-08Sd-0.2d^{2}}{D}
\Large S=\frac{L0-d}{n} (terra) \Large S=\frac{L0-2.5d}{n} (non lucidato)
|
|
Deformazione della molla di instabilità (valida per diversi coefficienti di supporto n, vedi EN 13906-1:2002) |
 |
Tutte le molle sollecitate dinamicamente con uno spessore del filo di > 1 mm devono essere pallinate. Questo aumenta la forza della corsa continua. Una volta effettuata la verifica funzionale e la verifica della resistenza, è necessario effettuare e prendere in considerazione diversi calcoli geometrici per poter inserire la molla nel progetto del componente. La lunghezza del blocco non può essere ridotta perché gli avvolgimenti sono saldamente collegati tra loro, mentre la lunghezza minima utilizzabile non deve essere ridotta perché in tal caso non sono più garantite la curva di forza lineare e la capacità di carico dinamico. È necessario tenere in considerazione anche le tolleranze ammesse dalla norma DIN 2095.
Calcolo delle molle di tensione
Informazioni generali
Le molle a trazione sono avvolte attorno a un mandrino esattamente come le molle a compressione, ma senza distanza tra le spire e con diverse forme di occhielli/estremità per il fissaggio della molla. Durante la produzione, gli avvolgimenti vengono pressati strettamente l’uno con l’altro. Questa pretensione interna F0 dipende dal rapporto di avvolgimento e non può essere rifinita a qualsiasi livello desiderato. Il software di calcolo WinFSB di Gutekunst Federn fornisce valori di riferimento per il livello di precarico dopo aver inserito i dati relativi alla molla.
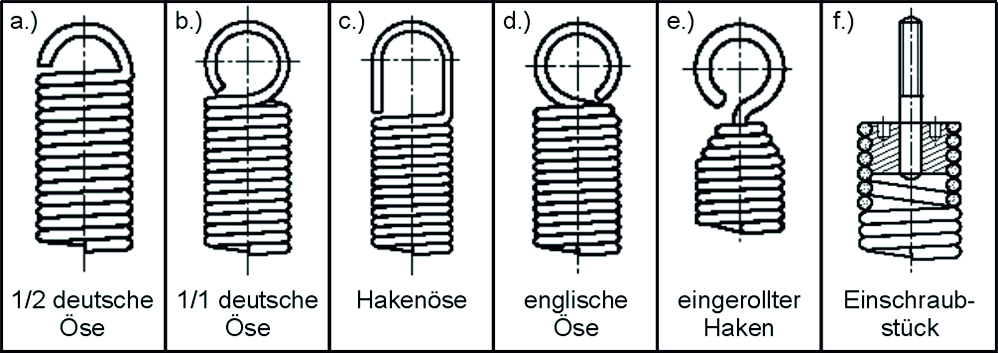
Immagine: Forme comuni di occhielli: a.) mezzo occhiello tedesco; b.) occhiello tedesco intero; c.) Occhio a gancio; d.) occhiello inglese; e.) gancio arrotolato; f.) Pezzo da avvitare
Il vantaggio delle molle a trazione è che sono prive di attorcigliamenti; gli svantaggi sono l’ingombro maggiore e la completa interruzione del flusso di forza quando la molla si rompe.
Formule di calcolo della molla a trazione cilindrica
In accordo con le equazioni di calcolo per le molle a compressione, ma tenendo conto della forza di precarico, le seguenti relazioni si applicano alle molle a trazione cilindriche in filo tondo (vedi anche la Figura 1.8):
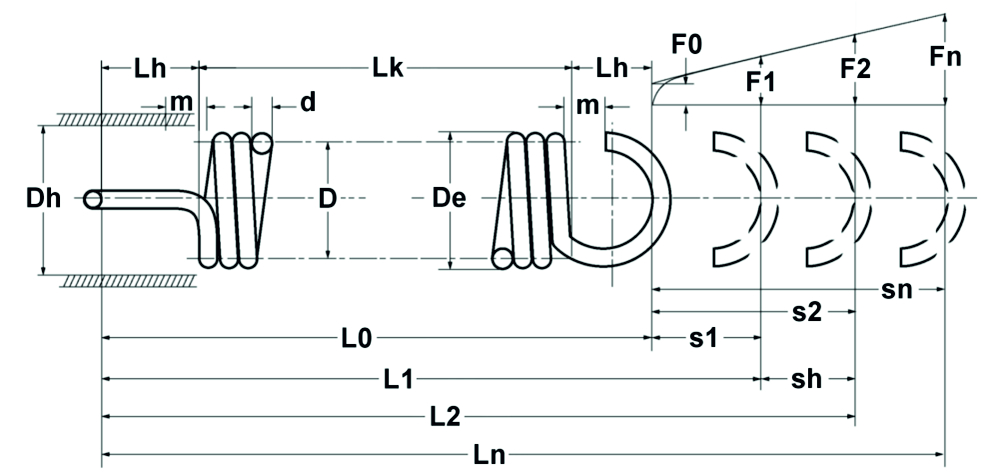
Figura: Diagramma teorico della molla di tensione
Prova di funzionamento della molla di tensione
Quanto segue si applica alle molle di trazione cilindriche realizzate con fili a sezione circolare:
Velocità della molla: \Large R=\frac{Gd^4}{8D^3n}=\frac{F-F0}{s}
segue da “R=F/s”:
Forza della molla: \Large F=\frac{Gd^4s}{8D^3n}+F0
e:
Corsa della molla: \Large s=\frac{8D^3n(F-F0)}{Gd^4}
Verifica della resistenza delle molle a trazione
Come per i calcoli delle molle a compressione, è necessario determinare lo sforzo di taglio esistente.
Sforzo di taglio: \Large \tau=\frac{8DF}{\pi d^3}
Lo sforzo di sollevamento corretto deve essere calcolato anche per i carichi dinamici.
Sforzo di taglio corretto: \Large \tau_{{k}}=k\tau
Tensione ammissibile: \Large \tau_{{zul}}=0,45 \cdot R_{{m}}
La tensione massima esistente t n per i viaggi più grandi n è impostato uguale alla tensione ammessa. Tuttavia, per evitare il rilassamento, nella pratica si dovrebbe utilizzare solo l’80% della corsa della sospensione.
\Large s_{{2}}=0,8 \cdot s_{{n}}Non è possibile specificare valori di resistenza alla fatica generalmente applicabili per carichi dinamici, poiché nei punti di flessione degli occhielli possono verificarsi sollecitazioni aggiuntive, alcune delle quali possono superare le sollecitazioni consentite. Le molle a trazione dovrebbero quindi essere sottoposte a carichi statici solo se possibile. Se lo stress dinamico non può essere evitato, si dovrebbe optare per l’angolo Occhielli fare a meno e utilizzare terminali arrotolati o avvitati. Un test di vita in condizioni operative successive ha senso. UN Indurimento superficiale mediante pallinatura non è fattibile a causa delle curve strette.
Relazioni geometriche per molle a trazione
| Caratteristica della primavera | Equazione di calcolo |
| Lunghezza del corpo | LK = (nt + 1)d |
| Lunghezza non sollecitata | L0 = LK + 2 LH |
| Altezza occhiello mezzo occhiello tedesco | LH = da 0,55Di a 0,80Di |
| Altezza occhiello occhiello tedesco intero | LH = da 0,80Di a 1,10Di |
| Altezza occhiello Occhiello di aggancio | LH > 1.10Di |
| Altezza occhiello Occhiello inglese | LH = 1,10Di |
È necessario rispettare le tolleranze di fabbricazione ammesse secondo la norma DIN 2097.
Calcolo delle molle di torsione (molle di torsione)
Informazioni generali
Le molle cilindriche a spirale (molle di torsione) hanno essenzialmente la stessa forma delle molle cilindriche a compressione e a trazione, ad eccezione delle estremità. Questi sono piegati a forma di gamba per consentire al corpo della molla di ruotare intorno all’asse della molla. Ciò significa che esistono diversi campi di applicazione, ad esempio come molle di ritorno o molle a cerniera. La molla di torsione deve essere montata su un mandrino di guida e il carico deve essere applicato solo nella direzione di avvolgimento. Questo riduce il diametro interno. Le molle sono solitamente avvolte senza passo. Tuttavia, se l’attrito è assolutamente indesiderato, le molle di torsione possono essere prodotte anche con una distanza tra le bobine. Nel caso di carichi dinamici, bisogna fare attenzione che non ci siano curve a spigolo vivo alle estremità delle molle per evitare picchi di stress imprevedibili.
Formule di calcolo per molle di torsione cilindriche (molle di torsione)
Il calcolo viene effettuato in conformità alle linee guida della norma EN 13906-3:2001:
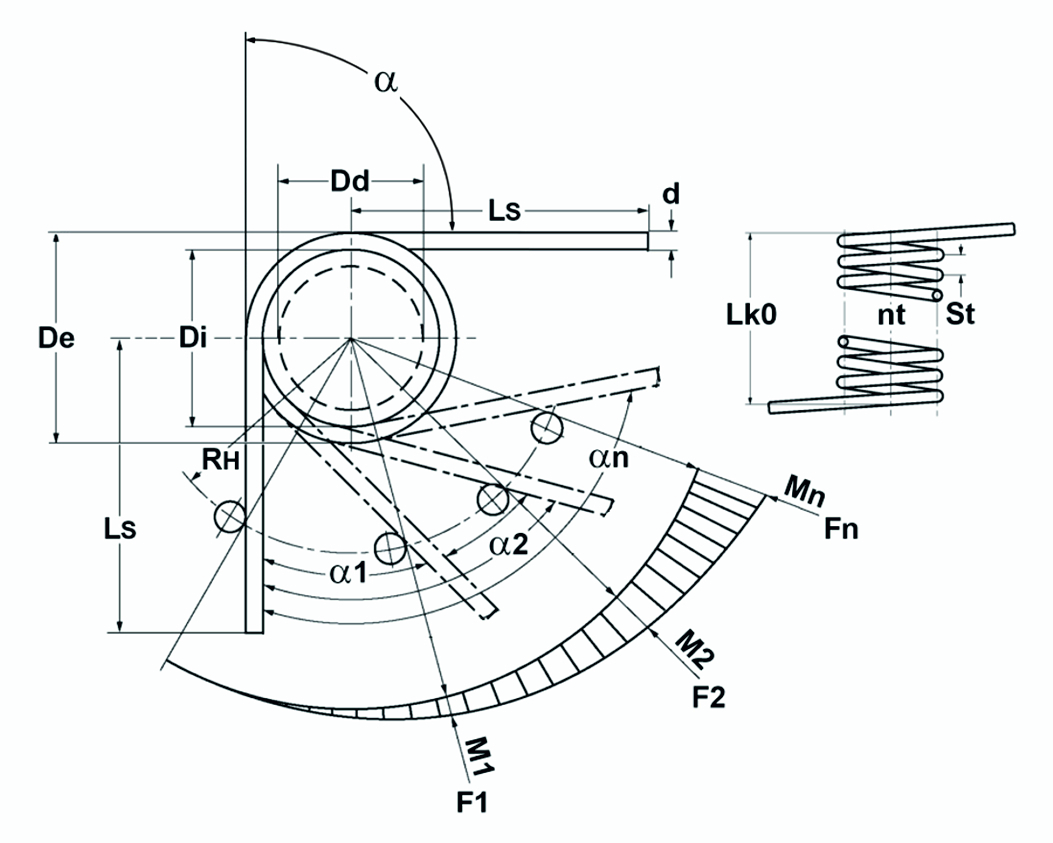
Figura: Diagramma teorico della molla di torsione / della molla di torsione
Verifica funzionale delle molle di torsione (molle di torsione)
Federmomentrato: \Large R_{M}=\frac{M}{\alpha}=\frac{d^4E}{3667Dn}
Momento di primavera: \Large M=FR_{H}=\frac{d^4E\alpha}{3667Dn}
Angolo di rotazione: \Large \alpha=\frac{3667DMn}{Ed^4}
Verifica della resistenza delle molle di torsione (molle di torsione)
La sollecitazione di flessione esistente viene determinata e confrontata con la sollecitazione ammissibile. Nel caso di sollecitazioni dinamiche, è necessario utilizzare la sollecitazione corretta per il confronto.
Sforzo di flessione: \Large \sigma=\frac{32M}{\pi d^3}
Sforzo di flessione corretto: \Large \sigma_{{q}}=q \sigma
dove q è valido:
\Large q=\frac{\frac{D}{d}+0.07}{\frac{D}{d}-0.75}
Sforzo di flessione ammissibile: \Large \sigma_{{zul}}=0,7Rm
A stress dinamico deve abbassare e aumentare la tensione (tk1 e tk2) della kcorsa corrispondente può essere determinata. La differenza è la tensione della corsa. Sia la tensione superiore che la tensione della corsa non devono superare i corrispondenti valori ammessi. Per il filo di acciaio per molle, questi valori sono riportati nei diagrammi di resistenza alla fatica della norma EN 13906-3:2001. Se le sollecitazioni resistono a questo confronto, la molla è resistente alla fatica con un ciclo di carico limite di 10 7 .
Relazioni geometriche per molle di torsione (molle di torsione)
| Caratteristica della primavera | Equazione di calcolo |
| Riduzione del diametro interno al massimo carico | \Large Di_{n}=\frac{Dn}{n+\frac{\alpha}{360}}-d |
| Lunghezza del corpo a vuoto | \Large Lk=(n+1,5)d |
| Lunghezza del corpo sotto carico massimo | \Large Lk_{n}=(n+1.5+\frac{\alpha}{360})d |
| Viaggio di primavera | \Large s_{n}= \frac{\alpha_{n}R_{H}}{57.3} |
Inoltre, è necessario tenere conto delle tolleranze di fabbricazione secondo la norma DIN 2194.
Una sintesi dell’articolo “Progettazione di una molla metallica”, composta dalla Parte 1 “Nozioni di base” e dalla Parte 2 “Calcolo”, può essere scaricata anche da Gutekunst Federn 1×1.
Se hai bisogno di un progetto di molla personalizzato, è sufficiente inviarci via e-mail i dati chiave della molla metallica che desideri a technik@gutekunst-co.com, contattare telefonicamente il nostro ufficio tecnico al numero (+49) 035877 227-11 o utilizzare il programma di calcolo delle molle di Gutekunst WinFSB all’indirizzo https://www.federnshop.com per calcolare gratuitamente molle a compressione, molle a trazione e molle a torsione.
Informazioni aggiuntive: