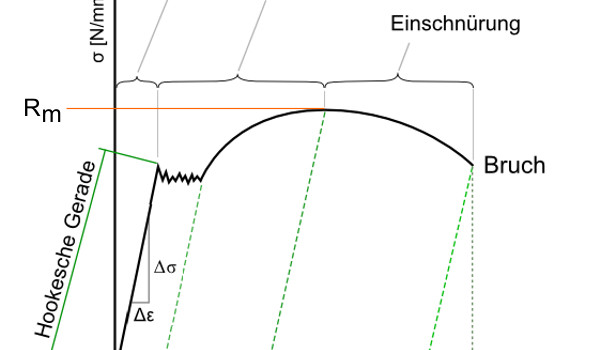
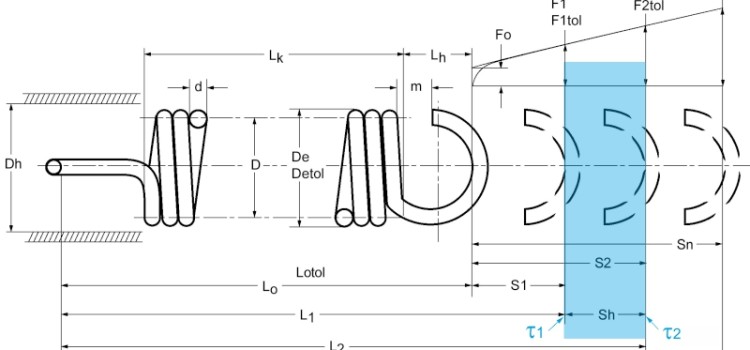
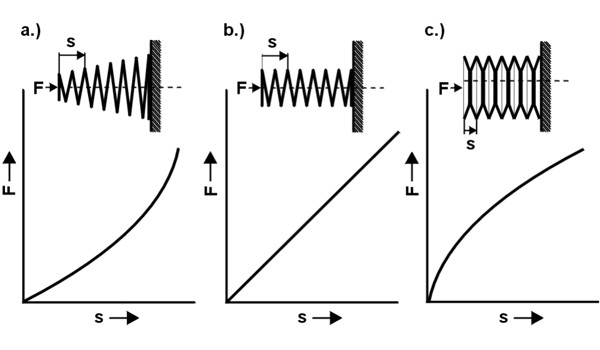
Wie wird eine Zugfeder hergestellt, welchen Einfluss haben Zugfeder-Bauformen, Ösenformen, Federkennlinie und Federwerkstoffe, und was bedeuten Fachbegriffe, wie Vorspannung, Relaxation, Dehngrenze und dynamische Belastung bei einer Zugfeder? Um für die nächste Zugfeder-Auslegung (Video) das Basiswissen etwas aufzufrischen geht Gutekunst Federn
Kompaktes Wissen rund um Zugfedern!