A kétrészes sorozat első részében a Gutekunst Federn a rugótervezés alapjairól adott tájékoztatást. Ebben a második részben találja a konkrét számítási adatokat a nyomórugók, a húzórugók és a torziós rugók (torziós rugók) tervezéséhez. A Gutekunst WinFSB rugószámítási programja egyedi számításokhoz is rendelkezésre áll.
A nyomórugó, húzórugó vagy torziós rugó tervezésének célja, hogy az adott feladatra minden körülményt figyelembe véve megtaláljuk a leggazdaságosabb rugót, amely a rendelkezésre álló helyre is befér, és eléri a kívánt élettartamot. A gyártási és anyagkövetelmények mellett különösen fontos a megfelelő rugókialakítás.
A rugó kiszámítása előtt össze kell állítani a fémrugó következő követelményeit:
1. a terhelés típusa (statikus vagy dinamikus)
2. élettartam
6. rendelkezésre álló beépítési hely
7. tűrések(nyomórugók, húzórugók)
8. beépítési helyzet (csavarodás, keresztirányú felfüggesztés)
Minden tavaszi számítás két szakaszból áll:
- Működés igazolása: a rugóerő, az erők és a rugóút, a rezgési viselkedés stb. ellenőrzése.
- Szilárdságvizsgálat
A megengedett feszültségeknek való megfelelés ellenőrzése vagy a fáradási szilárdság igazolása.
Ez iteratív megközelítést igényel.
A szilárdság ellenőrzése azon a döntésen alapul, hogy a rugót statikus, kvázi-statikus vagy dinamikus terhelésnek vetik-e alá. A megkülönböztetéshez a következő kritériumokat kell alkalmazni:
- Statikus vagy kvázi-statikus terhelés: állandó (statikus) terhelés az idő múlásával vagy változó terhelés az idő múlásával, összesen kevesebb, mint 10 000 löket.
- Dinamikus igénybevétel: időben változó terhelés több mint 10 000 lökésnél. A rugót általában előfeszítik, és szinuszos görbével periodikusan duzzadó terheléseknek vetik alá, amelyek véletlenszerűen (sztochasztikusan) jelentkeznek, pl. gépjárművek felfüggesztésében. Egyes esetekben hirtelen erőváltozások következnek be.
A rugók méretezésekor a terhelési határértékeket az anyagok szilárdsági értékei alapján és a terhelés típusának figyelembevételével kell meghatározni. A megengedett feszültség meghatározásához biztonsági tényezőt is figyelembe kell venni. A tényleges feszültséggel való összehasonlítás után a rugó méretezését iteratív eljárással felül kell vizsgálni. A következők érvényesek: Névleges feszültség ≤ megengedett feszültség
Table of Contents
Nyomórugók számítása
Általános információk
A gyakorlatban leggyakrabban az állandó osztású, hidegen alakított hengeres nyomórugókat használják. A huzalt hidegen alakítják úgy, hogy egy tüske köré tekerik. A tekercsek közötti távolság és a rugó érintkezési pontjai a menetszögtüske előtolási sebességétől függően szabályozhatók. A tekercselés után a rugóban lévő maradó feszültségek csökkentése és a nyírási rugalmassági határérték növelése érdekében temperálást végeznek. A beállítási összeg ezért csökken. Az edzési hőmérséklet és idő az anyagtól függ; a hűtés levegőn, normál szobahőmérsékleten történik.
A rugógyártás további fontos műveletei a csiszolás és a beállítás. A rugóvégek általában 0,5 mm vastagságú huzalból vannak lecsiszolva, hogy a rugó síkban párhuzamos alátámasztást és optimális erőátvitelt biztosítsanak.
Ha a nyírófeszültség meghaladja a rugó terhelésénél a megengedett értéket, maradandó deformáció lép fel, amely a feszültségmentes hossz csökkenésében nyilvánul meg. A rugótechnológiában ezt a folyamatot „beállításnak” nevezik, ami az anyagtechnológiából ismert „kúszás” és„lazulás” kifejezésekkel azonosítható. Ennek ellensúlyozására a nyomórugókat a várható beállítási értékkel hosszabbra tekercselik, majd később blokkhosszúra tömörítik. Ez az előzetes beállítás jobb anyagkihasználást tesz lehetővé, és a későbbi használat során nagyobb terhelést tesz lehetővé.
Számítási képletek hengeres nyomórugó
A nyomórugó számítása a DIN EN 13906-1 számítási egyenletein alapul:
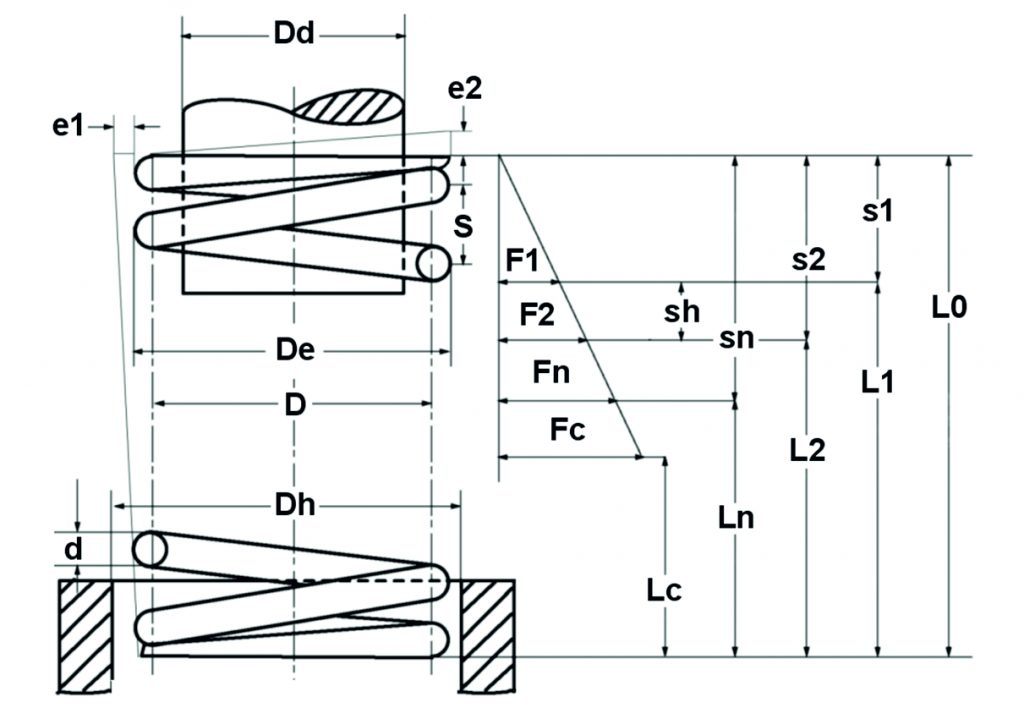
ábra: Elméleti nyomórugó diagram
A nyomórugók működésének bizonyítása
A következők a kör keresztmetszetű huzalból készült hengeres nyomórugókra vonatkoznak:
Formula rugóerősség: \Large R=\frac{ Gd^{4}}{8D^{3}n}
az „R=F/s” értékből következik:
Rugóerő : \Large F=\frac{ Gd^{4}s}{8D^{3}n}
és:
Felfüggesztési menet : \Large s=\frac{8D^{3}nF}{Gd^{4}}
Szilárdságvizsgálat tömörítő rugó
A rugó méreteinek meghatározása után ellenőrizni kell az szilárdságot. Ebből a célból a meglévő nyírófeszültséget határozzák meg:
Erőből származó feszültség: \Large \tau=\frac{8DF}{\pi d^{3}}
Feszültség az útvonalról: \Large \tau=\frac{Gds}{\pi n D^{2}}
Míg a τ nyírófeszültséget a statikusan vagy kvázi statikusan igénybevett rugók tervezésénél használják, addig a korrigált τk nyírófeszültség a dinamikusan igénybevettrugókra vonatkozik. A nyírófeszültség eloszlása a rugó huzalkeresztmetszetében egyenetlen, a legnagyobb feszültség a rugó belső átmérőjén jelentkezik. A rugó tekercselési arányától (az átlagos átmérő és a huzalvastagság arányától) függő k feszültségkorrekciós tényezővel a legnagyobb feszültség hozzávetőlegesen meghatározható. Dinamikusan terhelt nyomórugók esetében ez a következőket eredményezi
Korrigált nyírófeszültség: \Large \tau_{k}=k\tau
ahol a k-ra a következők vonatkoznak (Bergsträsser szerint):
\Large k=\frac{\frac{D}{d}+0.5}{\frac{D}{d}-0.75}Most az összehasonlítást a megengedett feszültséggel végezzük. Ezt a következőképpen határozzák meg:
Megengedett feszültség:
\Large \tau_{{zul}}=0.5\cdot R_{{m}}és
\Large \tau_{{czul}}=0.56\cdot R_{{m}}A. ÉrtékeiMinimális R szakítószilárdság m a huzal vastagságától függenek, és megtalálhatók a megfelelő anyagok szabványaiban.
Rendszerint lehetővé kell tenni a nyomórugók tömörítési hosszáig történő összenyomását, ezért a blokkhossznál megengedett feszültség t czul megfontolni.
Nál nél dinamikus stressz alsó és felső feszültségnek (t k 1. és t k 2) a megfelelő löket meghatározható. A különbség a löketfeszültség. A felső és a löketfeszültség sem haladhatja meg a megfelelő megengedett értékeket. Ezek megtalálhatók az EN 13906-1:2002 szabvány fáradási szilárdsági diagramjaiban. Ha a feszültségek ellenállnak ennek az összehasonlításnak, a rugó fáradtságálló, 10-es határterheléssel 7 .
Geometriai összefüggések a nyomórugókhoz
| Tavaszi jellemző | Számítási egyenlet |
| Tekercsek száma összesen | nt = n + 2 |
| A földrugó blokkhossza | Lc = nt dmax |
| A vágatlan rugó blokkhossza | Lc = (nt + 1,5)dmax |
| Legkisebb használható hossz | Ln = Lc +Sa |
| Feszítetlen hossz | L0 = Ln +sn |
| A tekercsek közötti legkisebb távolságok összege | \Large S_{a}=\left (0,0015 \frac{D^{2}}{d} + 0,1d \right )\cdot n |
| A külső átmérő bővülése terhelés alatt
hangmagasság |
\Large \triangle D_{e}=0,1\frac{S^{2}-08Sd-0,2d^{2}}{D}
\Large S=\frac{L0-d}{n} (föld) \Large S=\frac{L0-2.5d}{n} (csiszolatlan)
|
|
A rugóhajlítás (különböző n csapágyazási együtthatókra érvényes, lásd EN 13906-1:2002) |
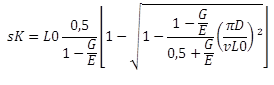 |
Minden dinamikusan igénybevett rugót, amelynek huzalvastagsága > 1 mm, lőtt hántolással kell kezelni. Ez növeli a folyamatos lökéserősséget. Miután mind a funkcionális, mind a szilárdsági ellenőrzést elvégezték, különböző geometriai számításokat kell végezni és figyelembe venni annak érdekében, hogy a rugót be lehessen illeszteni az alkatrész tervébe. A blokk hosszát nem lehet alávágni, mert a tekercsek szilárdan kapcsolódnak egymáshoz, a legkisebb használható hosszat nem szabad alávágni, mert akkor a lineáris erőgörbe és a dinamikus terhelhetőség már nem garantált. A DIN 2095 szerinti megengedett tűréshatárokat is figyelembe kell venni.
Feszített rugók számítása
Általános információk
A hosszabbító rugókat pontosan ugyanúgy tekerik egy tüske köré, mint a nyomórugókat, de a tekercsek között nincs távolság, és a rugó rögzítésére szolgáló különböző szemek/rugóvégek vannak kialakítva. A tekercseket a gyártás során szorosan egymáshoz préselik. Ez az F0 belső előfeszítés a tekercselési aránytól függ, és nem fejezhető be bármilyen kívánt szintre. A Gutekunst Federn WinFSB számítási szoftvere a vonatkozó rugóadatok megadása után referenciaértékeket ad az előfeszítés mértékére vonatkozóan.
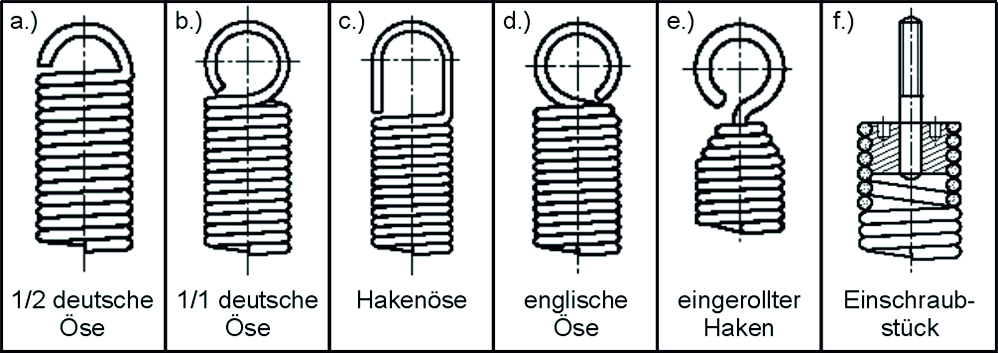
Kép: Gyakori szemcseformák: a.) fél német szemet; b.) egész német szemek; c.) Horgas szem; d.) angol szemet; e.) hengerelt horog; f.) Becsavarozható darab
A feszítőrugók előnye, hogy nem csomósodnak; hátrányuk a nagyobb beépítési hely és az erőáramlás teljes megszakadása a rugó törésekor.
Számítási képletek hengeres feszítőrugó
A nyomórugókra vonatkozó számítási egyenletekkel összhangban, de az előfeszítő erőt figyelembe véve, a következő összefüggések vonatkoznak a kerek huzalból készült hengeres húzórugókra (lásd még az 1.8. ábrát):
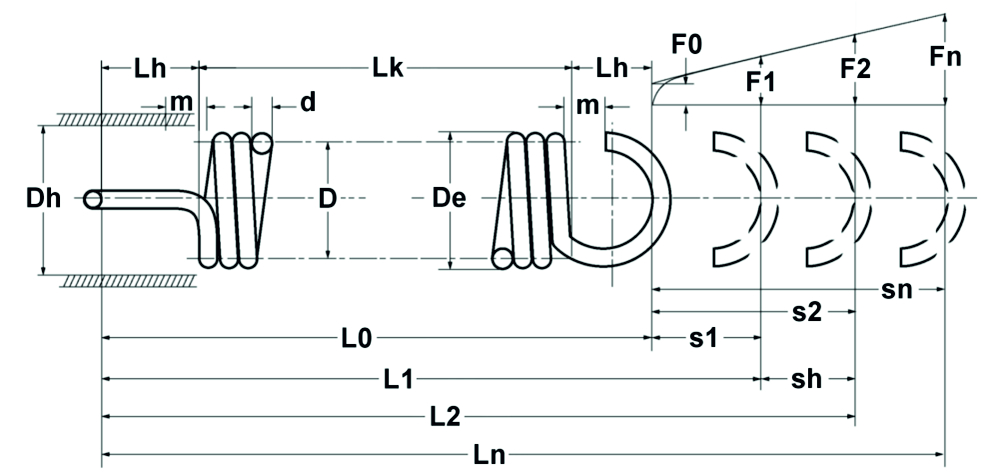
ábra: Elméleti feszültségrugó diagram
Funkcióbizonyítás feszítőrugó
A következők a kör keresztmetszetű huzalból készült hengeres húzórugókra vonatkoznak:
Tavaszi rugóerő: \Large R=\frac{Gd^4}{8D^3n}=\frac{F-F0}{s}
az R=F/s értékből következik:
Tavaszi erő: \Large F=\frac{Gd^4s}{8D^3n}+F0
és:
Tavaszi utazás: \Large s=\frac{8D^3n(F-F0)}{Gd^4}
Húzórugók szilárdságának ellenőrzése
A nyomórugó számításokhoz hasonlóan meg kell határozni a meglévő nyírófeszültséget.
Nyírófeszültség: \Large \tau=\frac{8DF}{\pi d^3}
A korrigált emelőfeszültséget dinamikus terhelésekre is ki kell számítani.
Korrigált nyírófeszültség: \Large \tau_{{k}}=k\tau
Megengedett feszültség: \Large \tau_{{zul}}=0,45 \cdot R_{{m}}
A meglévő maximális t feszültség n a legnagyobb utazáshoz s n a megengedett feszültséggel egyenlőre van beállítva. A lazulás elkerülése érdekében azonban a gyakorlatban ennek a felfüggesztési útnak csak 80 %-át kell kihasználni.
\Large s_{{2}}=0.8 \cdot s_{{n}}A dinamikus terhelésekre nem lehet általánosan alkalmazható fáradási szilárdsági értékeket meghatározni, mivel a szemek hajlítási pontjain további feszültségek léphetnek fel, amelyek közül néhány meghaladhatja a megengedett feszültségeket. A húzórugókat ezért lehetőleg csak statikus terhelésnek szabad kitenni. Ha a dinamikus stressz nem kerülhető el, akkor hajlítottnak kell lennie Fűzőlyukak csináld anélkül, és használj hengerelt vagy becsavart végdarabokat. A későbbi üzemi körülmények között életciklusnak van értelme. A A felület keményedése lövéscsiszolással a szűk fordulatok miatt nem megvalósítható.
Geometriai összefüggések a húzórugókhoz
| Tavaszi jellemző | Számítási egyenlet |
| Testhossz | LK = (nt + 1)d |
| Feszítetlen hossz | L0 = LK + 2 LH |
| Szemmagasság fél német szemlyuk | LH = 0,55Di és 0,80Di |
| Szemmagasság teljes német szemmagasság | LH = 0,80Di és 1,10Di |
| Szemmagasság Kampószem | LH > 1.10Di |
| Szemmagasság Angol szemlyuk magassága | LH = 1,10Di |
A DIN 2097 szerinti megengedett gyártási tűréseket be kell tartani.
Torziós rugók számítása (torziós rugók)
Általános információk
A tekercselt hengeres lábrugók (torziós rugók) lényegében ugyanolyan alakúak, mint a hengeres nyomó- és húzórugók, a rugóvégek kivételével. Ezek láb alakban hajlítottak, hogy a rugótest a rugó tengelye körül elfordulhasson. Ez azt jelenti, hogy számos különböző alkalmazási terület létezik, pl. visszatérő rugóként vagy csuklópántrugóként. A torziós rugót egy vezető tüskére kell szerelni, és a terhelést csak a tekercselés irányában kell alkalmazni. Ez csökkenti a belső átmérőt. A rugókat általában osztás nélkül tekerik fel. Ha azonban a súrlódás egyáltalán nem kívánatos, a torziós rugók tekercseltávolsággal is gyárthatók. Dinamikus terhelés esetén ügyelni kell arra, hogy a rugók végein ne legyenek éles szélű hajlítások, hogy elkerülhetők legyenek a kiszámíthatatlan feszültségcsúcsok.
Számítási képletek hengeres torziós rugókra (torziós rugók)
A számítás az EN 13906-3:2001 szabvány iránymutatásai szerint történik:
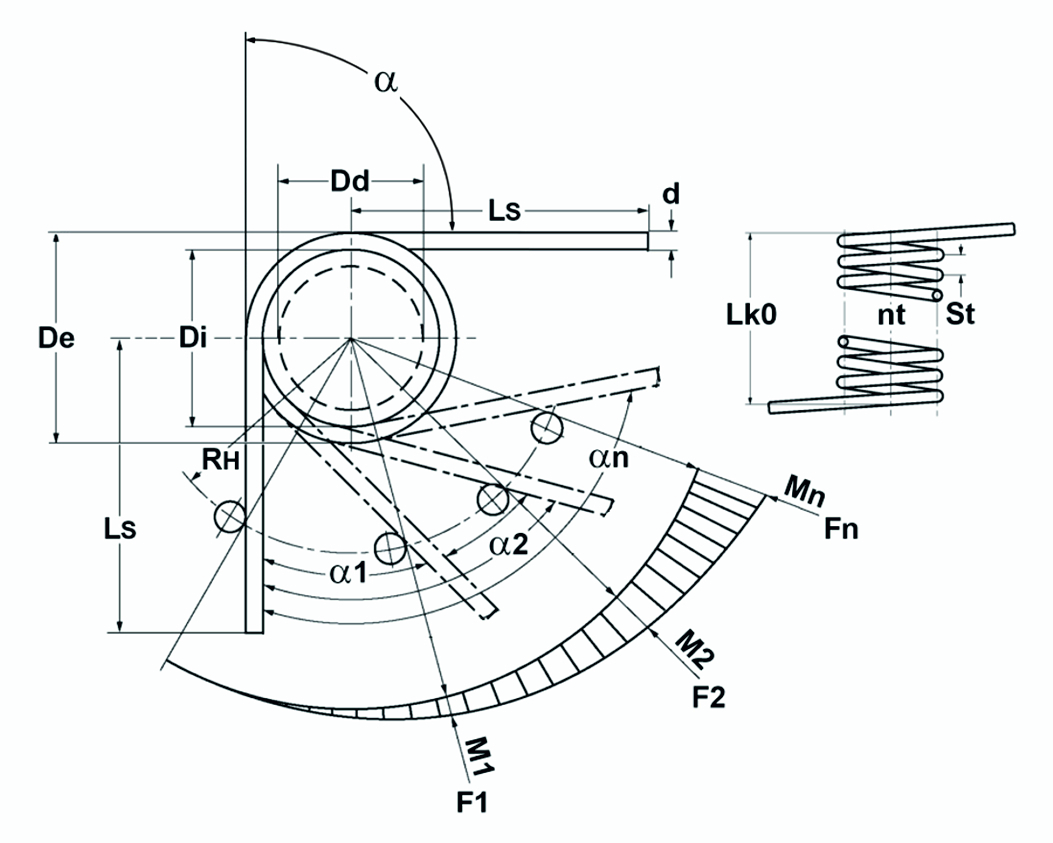
Ábra: Elméleti torziós rugó / torziós rugó diagramja
Torziós rugók működési ellenőrzése (torziós rugók)
Federmomentrát: \Large R_{M}=\frac{M}{\alpha}=\frac{d^4E}{3667Dn}
Tavaszi pillanat: \Large M=FR_{H}=\frac{d^4E\alpha}{3667Dn}
Forgatási szög: \Large \alpha=\frac{3667DMn}{Ed^4}
Torziós rugók (torziós rugók) szilárdságának ellenőrzése
A meglévő hajlítófeszültséget meghatározzák és összehasonlítják a megengedett feszültséggel. Dinamikus feszültség esetén az összehasonlításhoz ismét a korrigált feszültséget kell használni.
Hajlítófeszültség: \Large \sigma=\frac{32M}{\pi d^3}
Korrigált hajlítófeszültség: \Large \sigma_{{q}}=q \sigma
ahol q érvényes:
\Large q=\frac{\frac{D}{d}+0.07}{\frac{D}{d}-0.75}
Megengedett hajlítófeszültség: \Large \sigma_{{zul}}=0,7Rm
Nál nél dinamikus stressz alsó és felső feszültségnek (t k 1. és t k 2) a megfelelő löket meghatározható. A különbség a löketfeszültség. A felső és a löketfeszültség sem haladhatja meg a megfelelő megengedett értékeket. A rugóacélhuzalok esetében ezek az EN 13906-3:2001 szabvány fáradási szilárdsági diagramjaiban találhatók. Ha a feszültségek ellenállnak ennek az összehasonlításnak, a rugó fáradtságálló, 10-es határterheléssel 7. .
Geometriai összefüggések torziós rugókhoz (torziós rugók)
| Tavaszi jellemző | Számítási egyenlet |
| A belső átmérő csökkenése maximális terhelésnél | \Large Di_{n}=\frac{Dn}{n+\frac{\alpha}{360}}-d |
| Tehermentes testhossz | \Large Lk=(n+1,5)d |
| Testhossz maximális terhelés mellett | \Large Lk_{n}=(n+1,5+\frac{\alpha}{360})d |
| Tavaszi utazás | \Large s_{n}= \frac{\alpha_{n}R_{H}}{57.3} |
Ezenkívül figyelembe kell venni a DIN 2194 szerinti gyártási tűréseket is.
A „Fémrugó tervezése” című cikk összefoglalója, amely az 1. rész „Alapok” és a 2. rész „Számítás” című részéből áll, szintén letölthető a Gutekunst Federn 1×1 oldalról.
Ha egyedi rugótervezésre van szüksége, egyszerűen küldje el nekünk a technik@gutekunst-co.com címre a kívánt fémrugó főbb adatait , vagy vegye fel a kapcsolatot műszaki osztályunkkal a (+49) 035877 227-11-es telefonszámon, vagy használja a Gutekunst WinFSB rugószámítási programját a https://www.federnshop.com címen a nyomó-, húzó- és torziós rugók ingyenes kiszámításához.
További információ: