W pierwszej części tej dwuczęściowej serii Gutekunst Federn przedstawił informacje na temat podstaw projektowania sprężyn. W tej drugiej części znajdują się szczegółowe dane obliczeniowe do projektowania sprężyn naciskowych, naciągowych i skrętnych (sprężyn skrętnych). Program do obliczeń sprężyn Gutekunst WinFSB jest również dostępny do indywidualnych obliczeń.
Celem projektowania sprężyny naciskowej, naciągowej lub skrętnej jest znalezienie najbardziej ekonomicznej sprężyny do danego zadania, biorąc pod uwagę wszystkie okoliczności, która również mieści się w dostępnej przestrzeni i osiąga wymaganą żywotność. Oprócz tych wymagań produkcyjnych i materiałowych, szczególnie ważna jest prawidłowa konstrukcja sprężyny.
Przed obliczeniem sprężyny należy zestawić następujące wymagania dotyczące sprężyny metalowej:
1. rodzaj obciążenia (statyczne lub dynamiczne)
2. Lifetime
5. Wymagane siły i skok sprężyny
6. dostępna przestrzeń montażowa
7. tolerancje(sprężyny naciskowe, sprężyny naciągowe)
8. sytuacja montażowa (wyboczenie, zawieszenie poprzeczne)
Każde obliczenie sprężyny składa się z dwóch etapów:
- Weryfikacja funkcjonalna: Sprawdzanie współczynnika sprężyny, sił i skoku sprężyny, zachowania wibracyjnego itp.
- Weryfikacja wytrzymałości
Sprawdzenie zgodności z dopuszczalnymi naprężeniami lub dowód wytrzymałości zmęczeniowej.
Wymaga to podejścia iteracyjnego.
Weryfikacja wytrzymałości opiera się na decyzji, czy sprężyna jest poddawana obciążeniu statycznemu, quasi-statycznemu czy dynamicznemu. W celu rozróżnienia należy stosować następujące kryteria:
- Obciążenie statyczne lub quasi-statyczne: stałe (statyczne) obciążenie w czasie lub zmienne obciążenie w czasie o łącznej liczbie skoków poniżej 10 000.
- Naprężenia dynamiczne: obciążenia zmienne w czasie z ponad 10 000 skoków. Sprężyna jest zwykle wstępnie naprężona i poddawana okresowym obciążeniom pęczniejącym o krzywej sinusoidalnej, które występują losowo (stochastycznie), np. w zawieszeniach pojazdów silnikowych. W niektórych przypadkach występują nagłe zmiany siły.
Podczas wymiarowania sprężyn należy zdefiniować limity obciążenia w oparciu o wartości wytrzymałości materiałów i z uwzględnieniem rodzaju obciążenia. W celu określenia dopuszczalnego napięcia uwzględniono współczynnik bezpieczeństwa. Po porównaniu z rzeczywistym naprężeniem, wymiarowanie sprężyny musi zostać skorygowane przy użyciu procedury iteracyjnej. Obowiązuje następująca zasada: Napięcie nominalne ≤ napięcie dopuszczalne
Table of Contents
Obliczanie sprężyn ściskanych
Informacje ogólne
W praktyce najczęściej stosowane są formowane na zimno cylindryczne sprężyny naciskowe o stałym skoku. Drut jest formowany na zimno poprzez nawijanie go wokół trzpienia. Odległość między zwojami i styk sprężyny są regulowane w zależności od prędkości posuwu trzpienia podziałowego. Po zwinięciu przeprowadza się odpuszczanie w celu zmniejszenia naprężeń szczątkowych w sprężynie i zwiększenia granicy sprężystości przy ścinaniu. Kwota ustawienia jest zatem zmniejszona. Temperatura i czas odpuszczania zależą od materiału; chłodzenie odbywa się w powietrzu w normalnej temperaturze pokojowej.
Inne ważne operacje w produkcji sprężyn to szlifowanie i wiązanie. Końce sprężyny są zwykle szlifowane z drutu o grubości 0,5 mm w celu zapewnienia płasko-równoległego łożyskowania sprężyny i optymalnego przenoszenia siły.
Jeśli naprężenie ścinające przekracza dopuszczalną wartość, gdy sprężyna jest obciążona, następuje trwałe odkształcenie, które objawia się zmniejszeniem długości bez naprężenia. W technologii sprężyn proces ten określany jest jako „wiązanie”, co można utożsamiać z terminami „pełzanie” i„relaksacja” w technologii materiałowej. Aby temu przeciwdziałać, sprężyny dociskowe są zwijane dłużej o oczekiwaną wartość ustawienia, a następnie ściskane do długości bloku. To wstępne ustawienie umożliwia lepsze wykorzystanie materiału i pozwala na większe obciążenie w późniejszym użytkowaniu.
Wzory obliczeniowe cylindrycznej sprężyny naciskowej
Obliczenia sprężyny naciskowej opierają się na równaniach obliczeniowych z normy DIN EN 13906-1:
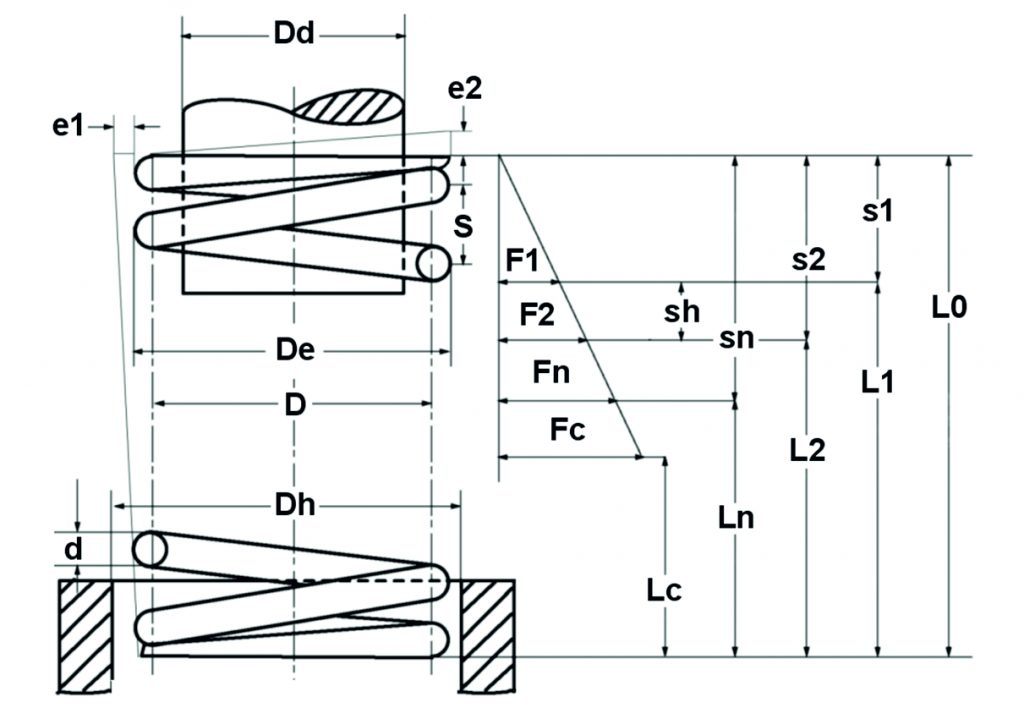
Rysunek: Teoretyczny schemat sprężyny naciskowej
Dowód działania sprężyn naciskowych
Poniższe dotyczy cylindrycznych sprężyn naciskowych wykonanych z drutu o przekroju kołowym:
Wzór na współczynnik sprężystości: \Large R=\frac{ Gd^{4}}{8D^{3}n}
wynika z „R=F/s”:
Siła sprężyny : \Large F=\frac{ Gd^{4}s}{8D^{3}n}
i:
Skok zawieszenia : \Large s=\frac{8D^{3}nF}{Gd^{4}}
Weryfikacja wytrzymałości sprężyny naciskowej
Po określeniu wymiarów sprężyny należy zweryfikować wytrzymałość. W tym celu określa się istniejące naprężenie ścinające:
Napięcie wynikające z siły: \Large \tau=\frac{8DF}{\pi d^{3}}
Napięcie ze ścieżki: \Large \tau=\frac{Gds}{\pi n D^{2}}
Podczas gdy naprężenie ścinające τ jest używane do projektowania sprężyn obciążonych statycznie lub quasi-statycznie, skorygowane naprężenie ścinające τk ma zastosowaniedo sprężyn obciążonych dynamicznie. Rozkład naprężeń ścinających w przekroju drutu sprężyny jest nierównomierny, największe naprężenia występują na średnicy wewnętrznej sprężyny. Przy pomocy współczynnika korekcji naciągu k, który zależy od stosunku zwojów (stosunku średniej średnicy do grubości drutu) sprężyny, można w przybliżeniu wyznaczyć największe naprężenie. W przypadku dynamicznie naprężonych sprężyn ściskanych skutkuje to
Skorygowane naprężenie ścinające: \Large \tau_{k}=k\tau
gdzie dla k (według Bergsträssera) obowiązuje następująca zależność:
\Large k=\frac{\frac{D}{d}+0.5}{\frac{D}{d}-0.75}Teraz porównanie jest dokonywane z dopuszczalnym napięciem. Jest to zdefiniowane w następujący sposób:
Dopuszczalne napięcie:
\Large \tau_{{zul}}=0.5\cdot R_{{m}}oraz
\Large \tau_{{czul}}=0.56\cdot R_{{m}}Wartości dlaMinimalna wytrzymałość na rozciąganie R m zależą od grubości drutu i można je znaleźć w normach odpowiednich materiałów.
Z reguły musi być możliwe ściskanie sprężyn ściskanych do długości bloku, dlatego dopuszczalne naprężenie przy długości bloku wynosi t czul do rozważenia.
W dynamiczny stres musi niższe i wyższe napięcie (tk1 i tk2) odpowiedniego skoku. Różnica to napięcie udaru. Zarówno naprężenie górne, jak i naprężenie skoku nie mogą przekraczać odpowiednich dopuszczalnych wartości. Można je znaleźć na wykresach wytrzymałości zmęczeniowej w normie EN 13906-1:2002. Jeśli naprężenia wytrzymają to porównanie, sprężyna jest odporna na zmęczenie z granicznym cyklem obciążenia równym 10 7 .
Zależności geometryczne dla sprężyn ściskanych
| Charakterystyka wiosenna | Równanie obliczeniowe |
| Całkowita liczba zwojów | nt = n + 2 |
| Długość bloku sprężyny uziemiającej | Lc = nt dmax |
| Długość bloku nieobciętej sprężyny | Lc = (nt + 1,5)dmax |
| Najmniejsza długość użytkowa | Ln = Lc +Sa |
| Długość bez naprężenia | L0 = Ln +sn |
| Suma minimalnych odległości między uzwojeniami | \Large S_{a}= \left (0.0015 \frac{D^{2}}{d} + 0.1d \right )\cdot n |
| Powiększenie średnicy zewnętrznej pod obciążeniem
smoła |
\Large \triangle D_{e}=0.1\frac{S^{2}-08Sd-0.2d^{2}}{D}
\Large S=\frac{L0-d}{n} (naziemny) \Large S=\frac{L0-2.5d}{n} (niepolerowane)
|
|
Ugięcie sprężyny wyboczeniowej (ważne dla różnych współczynników łożyska n, patrz EN 13906-1:2002) |
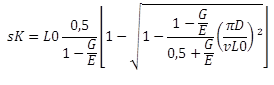 |
Wszystkie sprężyny obciążane dynamicznie o grubości drutu > 1 mm powinny być śrutowane. Zwiększa to siłę skoku ciągłego. Po przeprowadzeniu zarówno weryfikacji funkcjonalnej, jak i wytrzymałościowej, należy przeprowadzić i uwzględnić różne obliczenia geometrii, aby móc dopasować sprężynę do projektu komponentu. Długość bloku nie może być podcięta, ponieważ uzwojenia są ze sobą mocno połączone, najmniejsza użyteczna długość nie powinna być podcięta, ponieważ wtedy liniowa krzywa siły i dynamiczna nośność nie są już gwarantowane. Należy również wziąć pod uwagę dopuszczalne tolerancje zgodnie z normą DIN 2095.
Obliczanie sprężyn naciągowych
Informacje ogólne
Sprężyny rozciągane są nawijane wokół trzpienia w dokładnie taki sam sposób jak sprężyny naciskowe, ale bez odstępu między zwojami i z różnymi kształtami oczek/końcówek sprężyny do mocowania sprężyny. Uzwojenia są ściśle dociskane do siebie podczas produkcji. Wewnętrzne naprężenie wstępne F0 zależy od przełożenia uzwojenia i nie może być ustawione na dowolnym poziomie. Oprogramowanie obliczeniowe WinFSB firmy Gutekunst Federn zapewnia wartości referencyjne dla poziomu napięcia wstępnego po wprowadzeniu odpowiednich danych sprężyny.
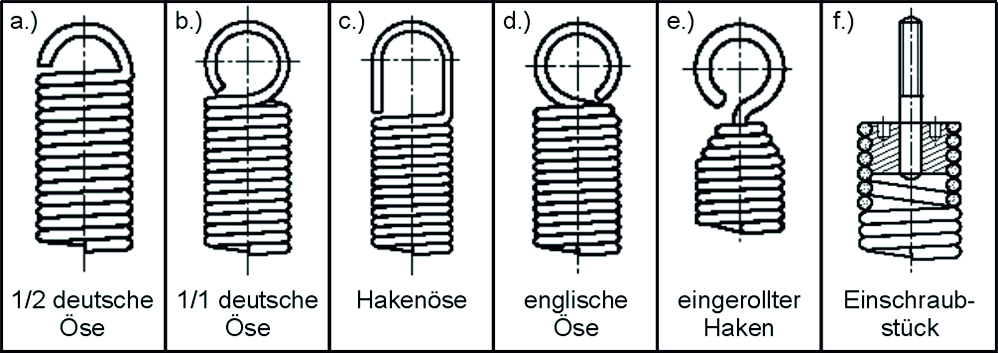
Zdjęcie: Typowe kształty oczek: a.) pół niemieckiego oczka; b.) całe niemieckie oczko; c.) Ucho haka; d.) Oczko angielskie; e.) zwinięty hak; f.) Element wkręcany
Zaletą sprężyn naciągowych jest brak załamań; wadą jest większa przestrzeń montażowa i całkowite przerwanie przepływu siły w przypadku pęknięcia sprężyny.
Wzory obliczeniowe cylindrycznej sprężyny naciągowej
Zgodnie z równaniami obliczeniowymi dla sprężyn ściskanych, ale z uwzględnieniem siły napięcia wstępnego, poniższe zależności mają zastosowanie do cylindrycznych sprężyn naciągowych wykonanych z drutu okrągłego (patrz również rysunek 1.8):
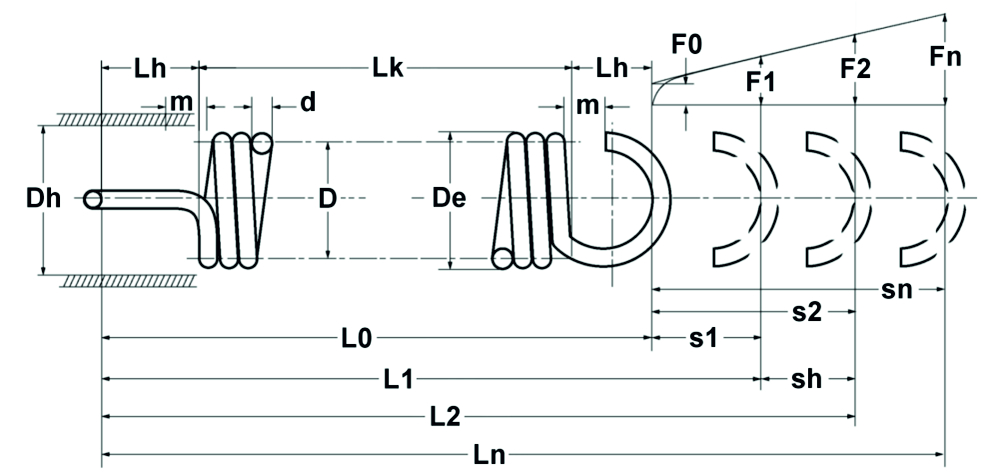
Rysunek: Teoretyczny schemat sprężyny naciągowej
Dowód działania sprężyny naciągowej
Poniższe dotyczy cylindrycznych sprężyn naciągowych wykonanych z drutu o przekroju kołowym:
Współczynnik sprężystości: \Large R=\frac{Gd^4}{8D^3n}=\frac{F-F0}{s}
wynika z R=F/s:
Siła sprężyny: \Large F=\frac{Gd^4s}{8D^3n}+F0
i:
Podróż sprężynowa: \Large s=\frac{8D^3n(F-F0)}{Gd^4}
Weryfikacja wytrzymałości sprężyn naciągowych
Podobnie jak w przypadku obliczeń sprężyn ściskanych, należy określić istniejące naprężenie ścinające.
Naprężenie ścinające: \Large \tau=\frac{8DF}{\pi d^3}
Skorygowane naprężenie podnoszące należy również obliczyć dla obciążeń dynamicznych.
Skorygowane naprężenie ścinające: \Large \tau_{{k}}=k\tau
Dopuszczalne napięcie: \Large \tau_{{zul}}=0,45 \cdot R_{{m}}
Istniejące maksymalne napięcie t n dla największych podróży s n jest równa dopuszczalnemu napięciu. Aby jednak uniknąć rozluźnienia, w praktyce należy wykorzystywać tylko 80% tego skoku zawieszenia.
\Large s_{{2}}=0.8 \cdot s_{{n}}Nie można określić ogólnie stosowanych wartości wytrzymałości zmęczeniowej dla obciążeń dynamicznych, ponieważ w punktach zginania oczek mogą wystąpić dodatkowe naprężenia, z których niektóre mogą przekraczać dopuszczalne naprężenia. Dlatego też sprężyny naciągowe powinny być poddawane obciążeniom statycznym tylko wtedy, gdy jest to możliwe. Jeśli nie można uniknąć dynamicznego stresu, należy wybrać kąt Oczka zrezygnować z końcówek walcowanych lub wkręcanych i stosować je. Test żywotności w późniejszych warunkach pracy ma sens. ZA Utwardzanie powierzchniowe poprzez śrutowanie nie jest wykonalne z powodu ciasnych zakrętów.
Zależności geometryczne dla sprężyn naciągowych
| Charakterystyka wiosenna | Równanie obliczeniowe |
| Długość ciała | LK = (nt + 1)d |
| Długość bez naprężenia | L0 = LK + 2 LH |
| Wysokość połowy niemieckiego oczka | LH = 0,55Di do 0,80Di |
| Wysokość całego niemieckiego oczka | LH = 0,80Di do 1,10Di |
| Wysokość oczka Oczko hakowe | LH > 1.10Di |
| Wysokość oczka Oczko angielskie | LH = 1,10Di |
Należy przestrzegać dopuszczalnych tolerancji produkcyjnych zgodnie z normą DIN 2097.
Obliczanie sprężyn skrętnych (sprężyn skrętnych)
Informacje ogólne
Zwijane sprężyny cylindryczne (sprężyny skrętne) mają zasadniczo taki sam kształt jak cylindryczne sprężyny ściskane i rozciągane, z wyjątkiem końców sprężyny. Są one wygięte w kształcie nogi, aby umożliwić obrót korpusu sprężyny wokół osi sprężyny. Oznacza to, że istnieje wiele różnych obszarów zastosowań, np. jako sprężyny powrotne lub sprężyny zawiasów. Sprężyna skrętna powinna być zamontowana na trzpieniu prowadzącym, a obciążenie powinno być przykładane tylko w kierunku nawijania. Zmniejsza to średnicę wewnętrzną. Sprężyny są zwykle nawijane bez podziałki. Jeśli jednak tarcie jest absolutnie niepożądane, sprężyny skrętne mogą być również produkowane z odstępami między zwojami. W przypadku obciążeń dynamicznych należy upewnić się, że na końcach sprężyn nie ma ostrych zagięć, aby uniknąć nieprzewidywalnych skoków naprężeń.
Wzory obliczeniowe dla cylindrycznych sprężyn skrętnych (sprężyn skrętnych)
Obliczenia są przeprowadzane zgodnie z wytycznymi normy EN 13906-3:2001:
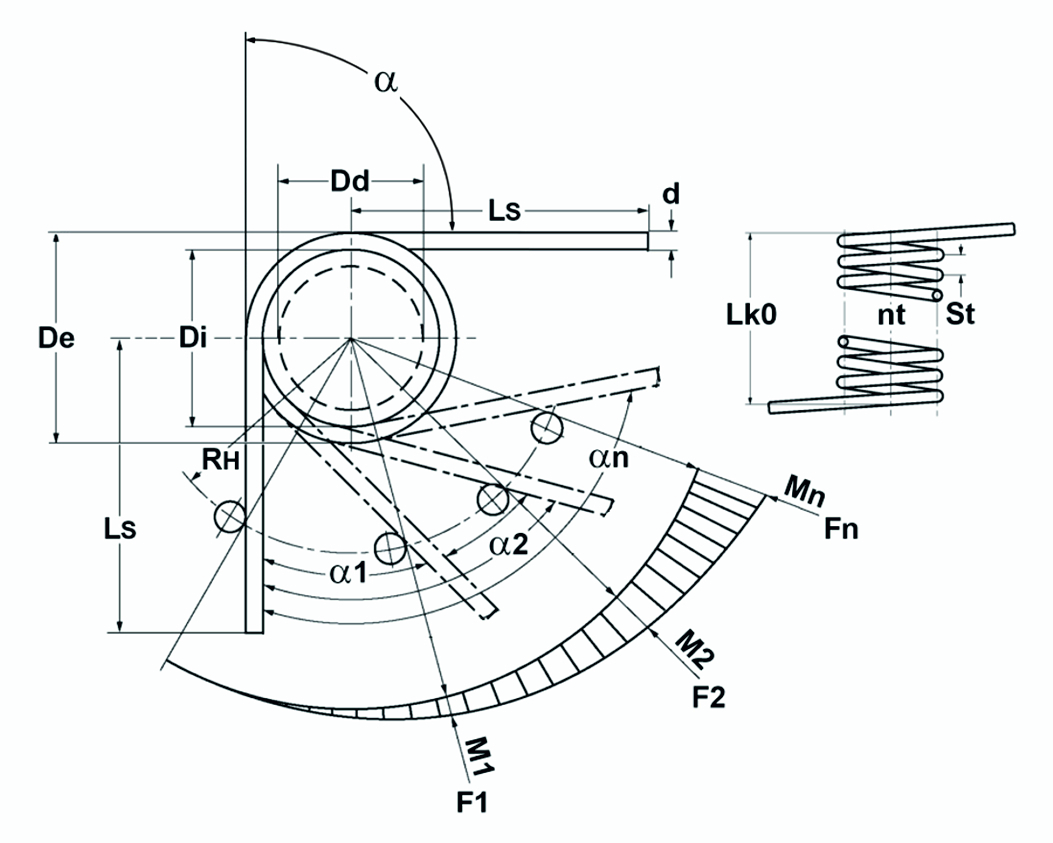
Rysunek: Teoretyczny schemat sprężyny skrętnej / sprężyny skrętnej
Weryfikacja funkcjonalna sprężyn skrętnych (sprężyn skrętnych)
Federmomentrate: \Large R_{M}=\frac{M}{\alpha}=\frac{d^4E}{3667Dn}
Wiosenny moment: \Large M=FR_{H}=\frac{d^4E\alpha}{3667Dn}
Kąt obrotu: \Large \alpha=\frac{3667DMn}{Ed^4}
Weryfikacja wytrzymałości sprężyn skrętnych (sprężyn skrętnych)
Istniejące naprężenie zginające jest określane i porównywane z naprężeniem dopuszczalnym. W przypadku naprężeń dynamicznych do porównania należy ponownie użyć naprężeń skorygowanych.
Naprężenie zginające: \Large \sigma=\frac{32M}{\pi d^3}
Skorygowane naprężenie zginające: \Large \sigma_{{q}}=q \sigma
gdzie q jest ważne:
\Large q=\frac{\frac{D}{d}+0.07}{\frac{D}{d}-0.75}
Dopuszczalne naprężenie zginające: \Large \sigma_{{zul}}=0,7Rm
W dynamiczny stres musi niższe i wyższe napięcie (tk1 i tk2) odpowiedniego skoku. Różnica to napięcie udaru. Zarówno naprężenie górne, jak i naprężenie skoku nie mogą przekraczać odpowiednich dopuszczalnych wartości. W przypadku drutu ze stali sprężynowej można je znaleźć na wykresach wytrzymałości zmęczeniowej w normie EN 13906-3:2001. Jeśli naprężenia wytrzymają to porównanie, sprężyna jest odporna na zmęczenie z granicznym cyklem obciążenia równym 10 7 .
Zależności geometryczne dla sprężyn skrętnych (sprężyn skrętnych)
| Charakterystyka wiosenna | Równanie obliczeniowe |
| Zmniejszenie średnicy wewnętrznej przy maksymalnym obciążeniu | \Large Di_{n}=\frac{Dn}{n+\frac{\alpha}{360}}-d |
| Długość korpusu bez obciążenia | \Large Lk=(n+1.5)d |
| Długość korpusu pod maksymalnym obciążeniem | \Large Lk_{n}=(n+1.5+\frac{\alpha}{360})d |
| Wiosenna podróż | \Large s_{n}= \frac{\alpha_{n}R_{H}}{57.3} |
Ponadto należy wziąć pod uwagę tolerancje produkcyjne zgodnie z normą DIN 2194.
Streszczenie artykułu „Projektowanie sprężyny metalowej”, składające się z części 1 „Podstawy” i części 2 „Obliczenia”, można również pobrać ze strony Gutekunst Federn 1×1.
Jeśli potrzebujesz niestandardowego projektu sprężyny, po prostu wyślij nam e-mailem kluczowe dane dotyczące metalowej sprężyny, której potrzebujesz, na adres technik@gutekunst-co.com, skontaktuj się z naszym działem technicznym telefonicznie pod numerem (+49) 035877 227-11 lub skorzystaj z programu do obliczania sprężyn Gutekunst WinFSB na stronie https://www.federnshop.com, aby bezpłatnie obliczyć sprężyny naciskowe, sprężyny naciągowe i sprężyny skrętne.
Dodatkowe informacje: